Rozwiązanie
Stopień statycznej niewyznaczalności
$$
\mathrm{SSN}=\mathrm{r}-3-\mathrm{p}+3 \cdot \mathrm{a}
$$
gdzie :
r - reakcje
p - przeguby
a - obwody zamknięte
\( \mathrm{SSN}=3-3-2+3 \cdot 1=1 \)
Liczba stopni swobody dynamicznej
\( \mathrm{LSSD}=3 \\ \quad \mathrm{~m}_1=100 \ kg \\ \quad \mathrm{m}_2=100\ kg \\ \quad \mathrm{m}_3=250\ kg
\)
przyjmując
\( \mathrm{m}=100 \mathrm{~kg} \)
\( m_1=m, \\ m_2=m, \\ m_3=2.5m \)
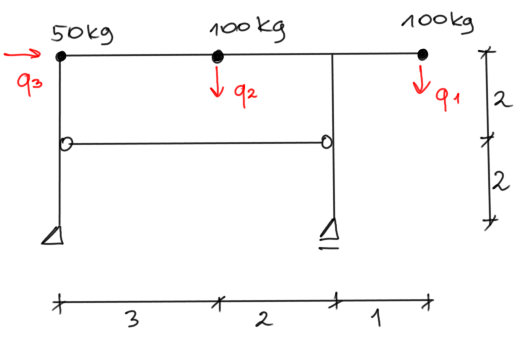
Ramę rozwiążemy METODĄ SIŁ.
Układ podstawowy metody sił
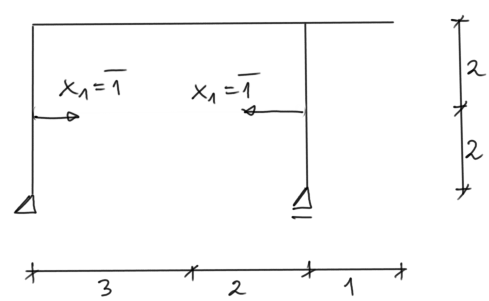
Wspólny stan jednostkowy
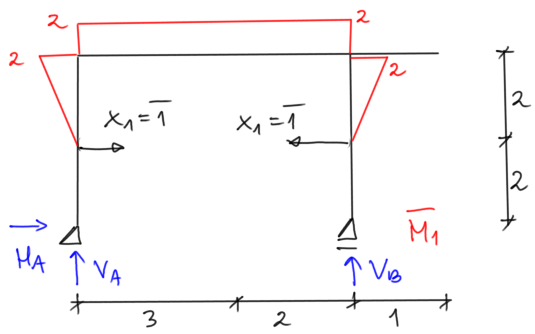
Reakcje
$$ \begin{aligned} &\Sigma \mathrm{M}_{\mathrm{A}}=0 \quad 1 \cdot 2-1 \cdot 2-\mathrm{V}_{\mathrm{B}} \cdot 5=0 \quad \mathrm{~V}_{\mathrm{B}}=0 \\ &\delta_{11}=\frac{1}{\mathrm{EI}} \cdot\left(\frac{1}{3} 2 \cdot 2 \cdot 2+2 \cdot 5 \cdot 2+\frac{1}{3} 2 \cdot 2 \cdot 2\right)=\frac{76}{3} \cdot \frac{1}{\mathrm{EI}} \end{aligned} $$ Teraz równolegle robimy stan P dla wszystkich przypadków obciążania, obliczamy całkowanie δ1p osobno dla każdego przypadku, obliczamy x1 (rozwiązujemy równanie kanoniczne) i rysujemy wykresy ostateczne.
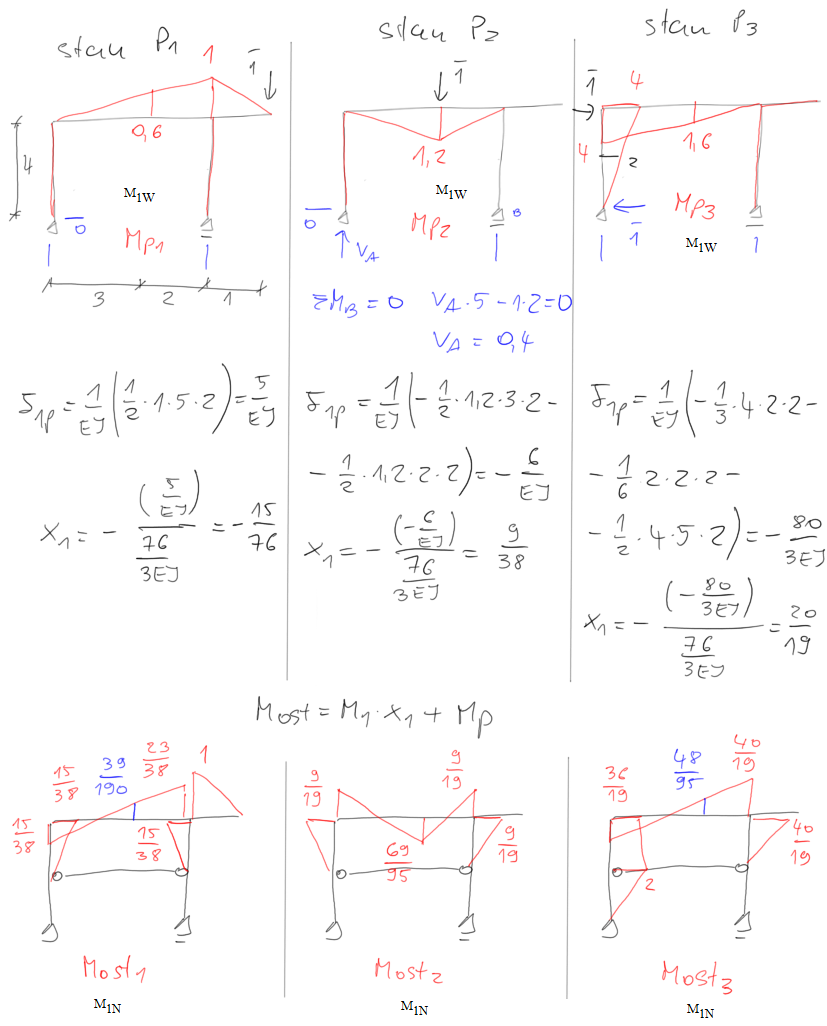
Delty dynamiczne z twierdzenia redukcyjnego $$ \begin{aligned} &\delta_{11}=\int \frac{\mathrm{M}_{\mathrm{Ost} 1} \cdot \mathrm{M}_{\mathrm{P} 1}}{\mathrm{EI}} \mathrm{dS} \\ &\delta_{11}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{5}{6} \cdot\left(2 \cdot 1 \cdot \frac{23}{38}-1 \cdot \frac{15}{38}\right)+\frac{1}{3} \cdot 1 \cdot 1 \cdot 1\right]=\frac{77}{76} \cdot \frac{1}{\mathrm{EI}} \end{aligned} $$ $$ \begin{aligned} &\delta_{22}=\int \frac{\mathrm{M}_{\mathrm{ost} 2} \cdot \mathrm{M}_{\mathrm{P} 2}}{\mathrm{EI}} \mathrm{dS} \\ &\delta_{22}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{3}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{69}{95}-1.2 \cdot \frac{9}{19}\right)+\frac{2}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{69}{95}-1.2 \cdot \frac{9}{19}\right)\right]=\frac{93}{95} \cdot \frac{1}{\mathrm{EI}} \end{aligned} $$ $$ \begin{aligned} &\delta_{33}=\int \frac{\mathrm{M}_{\mathrm{ost} 3} \cdot \mathrm{M}_{\mathrm{P} 3}}{\mathrm{EI}} \mathrm{dS} \\ &\delta_{33}=\frac{1}{\mathrm{EI}} \cdot\left[\begin{array}{l} \frac{1}{3} \cdot 2 \cdot 2 \cdot 2+\frac{2}{6} \cdot\left(2 \cdot 2 \cdot 2+2 \cdot \frac{36}{19} \cdot 4+\frac{36}{19} \cdot 2+4 \cdot 2\right) \ldots \\ +\frac{5}{6} \cdot\left(2 \cdot 4 \cdot \frac{36}{19}-4 \cdot \frac{40}{19}\right) \end{array}\right]=\frac{1136}{57} \cdot \frac{1}{\mathrm{EI}} \end{aligned} $$ $$ \begin{aligned} &\delta_{12}=\int \frac{\mathrm{M}_{\mathrm{ost} 1} \cdot \mathrm{M}_{\mathrm{P} 2}}{\mathrm{EI}} \mathrm{dS} \\ &\delta_{12}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{3}{6} \cdot\left(-2 \cdot 1.2 \cdot \frac{39}{190}+1.2 \cdot \frac{15}{38}\right)-\frac{2}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{39}{190}+1.2 \cdot \frac{23}{38}\right)\right]=-\frac{79}{190} \cdot \frac{1}{\mathrm{EI}} \quad \delta_{21}=\delta_{12} \end{aligned} $$ $$ \begin{aligned} &\delta_{13}=\int \frac{\mathrm{M}_{\mathrm{ost} 3} \cdot \mathrm{M}_{\mathrm{P} 1}}{\mathrm{EI}} \mathrm{dS} \\ &\delta_{13}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{5}{6} \cdot\left(2 \cdot 1 \cdot \frac{40}{19}-1 \cdot \frac{36}{19}\right)\right]=\frac{110}{57} \cdot \frac{1}{\mathrm{EI}} \quad \delta_{31}=\delta_{13} \\ &\delta_{23}=\int \frac{\mathrm{M}_{\mathrm{Ost} 3} \cdot \mathrm{M}_{\mathrm{P} 2}}{\mathrm{EI}} \mathrm{dS} \\ &\delta_{23}=\frac{1}{\mathrm{EI}}\left[\frac{3}{6} \cdot\left(-2 \cdot 1.2 \cdot \frac{48}{95}+1 \cdot 2 \cdot \frac{36}{19}\right)-\frac{2}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{48}{95}+1.2 \cdot \frac{40}{19}\right)\right]=-\frac{68}{95} \cdot \frac{1}{\mathrm{EI}} \quad \delta_{32}=\delta_{23} \end{aligned} $$ przyjmuję \( \mathrm{m}=100 \mathrm{~kg} \quad \mathrm{~m}_1=1 \mathrm{~m} \quad \mathrm{~m}_2=1 \mathrm{~m} \quad \mathrm{~m}_3=2.5 \mathrm{~m} \)
\( \left[\begin{array}{ccc} 1 \cdot \frac{77}{76}-x & 1 \cdot\left(-\frac{79}{190}\right) & \frac{5}{2} \cdot \frac{110}{57} \\ 1 \cdot\left(-\frac{79}{190}\right) & 1 \cdot \frac{93}{95}-x & \frac{5}{2}\left(\frac{68}{95}\right) \\ 1 \cdot \frac{110}{57} & 1 \cdot\left(\frac{68}{95}\right) & \frac{5}{2} \cdot \frac{1136}{57}-x \end{array}\right]=0 \)
\( \left[\begin{array}{llc} \frac{77}{76}-\mathrm{x} & -\frac{79}{190} & \frac{275}{57} \\ -\frac{79}{190} & \frac{93}{95}-\mathrm{x} & -\frac{34}{19} \\ \frac{110}{57} & -\frac{68}{95} & \frac{2840}{57}-\mathrm{x} \end{array}\right]=0 \)
Następnie należy metodą Sarrusa obliczyć wyznacznik z powyższej macierzy 3x3 i uprościć go do postaci wielomianu 3-go stopnia (jak poniżej). Najlepiej jeśli mamy do dyspozycji jakiś program, który może nam to uprościć, np. Mathcad.
\( -1 \cdot x^3+51.8167 \cdot x^2-89.4833 \cdot x+33.2632=0 \)
Pierwiastki równania $$ \mathrm{x}_1=0.537 \quad \mathrm{x}_2=1.238 \quad \mathrm{x}_3=50.042 $$ ponieważ \( \mathrm{x}=\frac{1}{\omega^2} \frac{\text { EI }}{\mathrm{m}} \quad \omega=\frac{1}{\sqrt{\mathrm{x}}} \cdot \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}} \)
Częstości drgań własnych
$$ \begin{aligned} &\omega_1=\frac{1}{\sqrt{x_3}}=0.14136 \cdot \sqrt{\frac{\text { EI }}{\mathrm{m}}} \\ &\omega_2=\frac{1}{\sqrt{x_2}}=0.899 \cdot \sqrt{\frac{E I}{\mathrm{~m}}} \\ &\omega_3=\frac{1}{\sqrt{x_1}}=1.3647 \cdot \sqrt{\frac{E I}{\mathrm{~m}}} \end{aligned} $$ Sztywność na zginanie $$ \begin{aligned} &\text { Dla } \quad \mathrm{I}=2140 \cdot 10^{-8} \mathrm{~m}^4 \quad \text { i modułu Younga dla stali } \quad \mathrm{E}=200 \cdot 10^9 \mathrm{~Pa} \\ &\mathrm{EI}=\mathrm{E} \cdot \mathrm{I}=4280000.000 \mathrm{Nm}^2 \quad \mathrm{~m}=100 \quad \mathrm{~kg} \\ &\omega_{1}=0.14136 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}=29.245 \quad \frac{\mathrm{rad}}{\mathrm{s}} \\ &\omega_{2}=0.899 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}=185.939 \frac{\mathrm{rad}}{\mathrm{s}} \\ &\omega_{3}=1.365 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}=282.33 \quad \frac{\mathrm{rad}}{\mathrm{s}} \end{aligned} $$
Wyznaczenie postaci drgań $$ \begin{aligned} &\left(\mathrm{m}_1 \cdot \delta_{11}-\mathrm{x}\right) \cdot \mathrm{A}_{11}+\mathrm{m}_2 \cdot \delta_{12} \cdot \mathrm{A}_{21}+\mathrm{m}_3 \cdot \delta_{13} \cdot \mathrm{A}_{31}=0 \\ &\mathrm{~m}_1 \cdot \delta_{12} \cdot \mathrm{A}_{11}+\left(\mathrm{m}_2 \cdot \delta_{22}-\mathrm{x}\right) \cdot \mathrm{A}_{21}+\mathrm{m}_3 \cdot \delta_{23} \cdot \mathrm{A}_{31}=0 \\ &\mathrm{~m}_1 \cdot \delta_{31} \cdot \mathrm{A}_{11}+\mathrm{m}_2 \cdot \delta_{32} \cdot \mathrm{A}_{21}+\left(\mathrm{m}_3 \cdot \delta_{33}-\mathrm{x}\right) \cdot \mathrm{A}_{31}=0 \end{aligned} $$
Taki układ równań jak powyżej rozwiążemy trzy razy, albowiem raz za "x" podstawimy "x1", raz "x2" i raz "x3".
Po podstawieniu x, mamy układ 3 równań z trzema niewiadomymi A11, A21, A31. Ten układ równań zawsze ma nieskończenie wiele rozwiązań,
musimy więc pokazać jedno przykładowe rozwiązanie. To znaczy założymy za jedną z niewiadomych wartość równą 1, i zostanie nam układ 3 równań z dwoma niewiadomymi, gdzie jak rozwiążemy układ dwóch pierwszych równań to obliczymy pozostałe dwie niewiadome.
dla \( \quad \mathrm{x}=\mathrm{x}_1=0.537 \quad zakładam \quad \mathrm{A}_{11}=1 \)
$$ \begin{aligned} &0.476+0.416 \mathrm{~A}_{21}+4.825 \cdot \mathrm{A}_{31}=0 \\ &-0.416+0.442 \mathrm{~A}_{21}-1.7895 \cdot \mathrm{A}_{31}=0 \\ &1.9298-0.716 \cdot \mathrm{A}_{21}+49.288 \cdot \mathrm{A}_{31}=0 \end{aligned} $$ Rozwiązuję układ dwóch pierwszych równań
$$ \begin{aligned} &\mathrm{A}_{21}=0.831 \\ &\mathrm{~A}_{31}=-0.027 \end{aligned} $$ I postać drgań
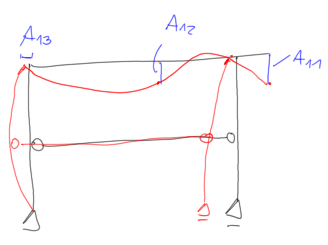
dla \( \quad \mathrm{x}=\mathrm{x}_2=1.238 \quad zakładam \quad \mathrm{A}_{12}=1 \)
$$ \begin{aligned} &-0.225-0.416 \cdot \mathrm{A}_{22}+4.825 \cdot \mathrm{A}_{32}=0 \\ &-0.416-0.259 \cdot \mathrm{A}_{22}-1.7895 \cdot \mathrm{A}_{32}=0 \\ &1.9298-0.716 \cdot \mathrm{A}_{22}+48.587 \cdot \mathrm{A}_{32}=0 \end{aligned} $$ Rozwiązuję układ dwóch pierwszych równań
$$ \begin{aligned} &\mathrm{A}_{22}=-1.208 \\ &\mathrm{~A}_{32}=-0.0575 \end{aligned} $$ II postać drgań
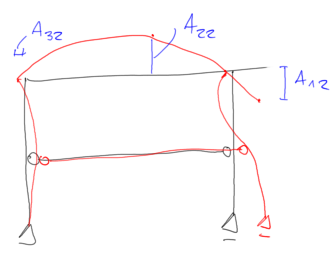
dla \( \quad \mathrm{x}=\mathrm{x}_3=50.042 \quad zakładam \quad \mathrm{A}_{13}=1 \)
$$ \begin{gathered} -49.0286-0.416 \cdot \mathrm{A}_{23}+4.825 \cdot \mathrm{A}_{33}=0 \\ -0.416-49.063 \cdot \mathrm{A}_{23}-1.7895 \cdot \mathrm{A}_{33}=0 \\ 1.9298-0.716 \cdot \mathrm{A}_{23}-0.217 \cdot \mathrm{A}_{33}=0 \end{gathered} $$ Rozwiązuję układ dwóch pierwszych równań
$$ \begin{aligned} &\mathrm{A}_{23}=-0.378 \\ &\mathrm{~A}_{33}=10.130 \end{aligned} $$ III postać drgań
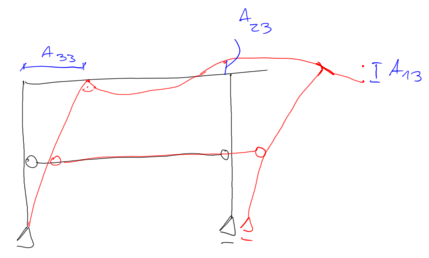
Sprawdzenie warunków ortogonalności
\begin{aligned} &\mathrm{m}_1 \cdot \mathrm{A}_{11} \cdot \mathrm{A}_{12}+\mathrm{m}_2 \cdot \mathrm{A}_{21} \cdot \mathrm{A}_{22}+\mathrm{m}_3 \cdot \mathrm{A}_{31} \cdot \mathrm{A}_{32}=0 \\ &\mathrm{~m}_1 \cdot \mathrm{A}_{12} \cdot \mathrm{A}_{13}+\mathrm{m}_2 \cdot \mathrm{A}_{22} \cdot \mathrm{A}_{23}+\mathrm{m}_3 \cdot \mathrm{A}_{32} \cdot \mathrm{A}_{33}=0 \\ &\mathrm{~m}_1 \cdot \mathrm{A}_{11} \cdot \mathrm{A}_{13}+\mathrm{m}_2 \cdot \mathrm{A}_{21} \cdot \mathrm{A}_{23}+\mathrm{m}_3 \cdot \mathrm{A}_{31} \cdot \mathrm{A}_{33}=0 \\ \end{aligned}
\begin{aligned} &1 \cdot 1 \cdot \mathrm{m}+1 \mathrm{~m} \cdot 0.831 \cdot(-1.208)+2.5 \mathrm{~m} \cdot(-0.027) \cdot(-0.0575) \rightarrow 0.00003 \mathrm{~m} \sim 0 \\ &1 \cdot 1 \cdot \mathrm{m}+1 \mathrm{~m} \cdot 0.831 \cdot(-1.208)+2.5 \mathrm{~m} \cdot(-0.027) \cdot(-0.0575) \rightarrow 0.00003 \mathrm{~m} \sim 0 \\ &1 \cdot 1 \cdot \mathrm{m}+1 \mathrm{~m} \cdot 0.831 \cdot(-0.378)+2.5 \mathrm{~m} \cdot(-0.027) \cdot 10.1297 \rightarrow 0.00213 \mathrm{~m} \sim 0 \end{aligned}
sprawdzenie daje pozytywny wynik
r - reakcje
p - przeguby
a - obwody zamknięte
\( \mathrm{SSN}=3-3-2+3 \cdot 1=1 \)
Liczba stopni swobody dynamicznej
\( \mathrm{LSSD}=3 \\ \quad \mathrm{~m}_1=100 \ kg \\ \quad \mathrm{m}_2=100\ kg \\ \quad \mathrm{m}_3=250\ kg
\)
przyjmując
\( \mathrm{m}=100 \mathrm{~kg} \)
\( m_1=m, \\ m_2=m, \\ m_3=2.5m \)

Ramę rozwiążemy METODĄ SIŁ.
Układ podstawowy metody sił

Wspólny stan jednostkowy

Reakcje
$$ \begin{aligned} &\Sigma \mathrm{M}_{\mathrm{A}}=0 \quad 1 \cdot 2-1 \cdot 2-\mathrm{V}_{\mathrm{B}} \cdot 5=0 \quad \mathrm{~V}_{\mathrm{B}}=0 \\ &\delta_{11}=\frac{1}{\mathrm{EI}} \cdot\left(\frac{1}{3} 2 \cdot 2 \cdot 2+2 \cdot 5 \cdot 2+\frac{1}{3} 2 \cdot 2 \cdot 2\right)=\frac{76}{3} \cdot \frac{1}{\mathrm{EI}} \end{aligned} $$ Teraz równolegle robimy stan P dla wszystkich przypadków obciążania, obliczamy całkowanie δ1p osobno dla każdego przypadku, obliczamy x1 (rozwiązujemy równanie kanoniczne) i rysujemy wykresy ostateczne.

Delty dynamiczne z twierdzenia redukcyjnego $$ \begin{aligned} &\delta_{11}=\int \frac{\mathrm{M}_{\mathrm{Ost} 1} \cdot \mathrm{M}_{\mathrm{P} 1}}{\mathrm{EI}} \mathrm{dS} \\ &\delta_{11}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{5}{6} \cdot\left(2 \cdot 1 \cdot \frac{23}{38}-1 \cdot \frac{15}{38}\right)+\frac{1}{3} \cdot 1 \cdot 1 \cdot 1\right]=\frac{77}{76} \cdot \frac{1}{\mathrm{EI}} \end{aligned} $$ $$ \begin{aligned} &\delta_{22}=\int \frac{\mathrm{M}_{\mathrm{ost} 2} \cdot \mathrm{M}_{\mathrm{P} 2}}{\mathrm{EI}} \mathrm{dS} \\ &\delta_{22}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{3}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{69}{95}-1.2 \cdot \frac{9}{19}\right)+\frac{2}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{69}{95}-1.2 \cdot \frac{9}{19}\right)\right]=\frac{93}{95} \cdot \frac{1}{\mathrm{EI}} \end{aligned} $$ $$ \begin{aligned} &\delta_{33}=\int \frac{\mathrm{M}_{\mathrm{ost} 3} \cdot \mathrm{M}_{\mathrm{P} 3}}{\mathrm{EI}} \mathrm{dS} \\ &\delta_{33}=\frac{1}{\mathrm{EI}} \cdot\left[\begin{array}{l} \frac{1}{3} \cdot 2 \cdot 2 \cdot 2+\frac{2}{6} \cdot\left(2 \cdot 2 \cdot 2+2 \cdot \frac{36}{19} \cdot 4+\frac{36}{19} \cdot 2+4 \cdot 2\right) \ldots \\ +\frac{5}{6} \cdot\left(2 \cdot 4 \cdot \frac{36}{19}-4 \cdot \frac{40}{19}\right) \end{array}\right]=\frac{1136}{57} \cdot \frac{1}{\mathrm{EI}} \end{aligned} $$ $$ \begin{aligned} &\delta_{12}=\int \frac{\mathrm{M}_{\mathrm{ost} 1} \cdot \mathrm{M}_{\mathrm{P} 2}}{\mathrm{EI}} \mathrm{dS} \\ &\delta_{12}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{3}{6} \cdot\left(-2 \cdot 1.2 \cdot \frac{39}{190}+1.2 \cdot \frac{15}{38}\right)-\frac{2}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{39}{190}+1.2 \cdot \frac{23}{38}\right)\right]=-\frac{79}{190} \cdot \frac{1}{\mathrm{EI}} \quad \delta_{21}=\delta_{12} \end{aligned} $$ $$ \begin{aligned} &\delta_{13}=\int \frac{\mathrm{M}_{\mathrm{ost} 3} \cdot \mathrm{M}_{\mathrm{P} 1}}{\mathrm{EI}} \mathrm{dS} \\ &\delta_{13}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{5}{6} \cdot\left(2 \cdot 1 \cdot \frac{40}{19}-1 \cdot \frac{36}{19}\right)\right]=\frac{110}{57} \cdot \frac{1}{\mathrm{EI}} \quad \delta_{31}=\delta_{13} \\ &\delta_{23}=\int \frac{\mathrm{M}_{\mathrm{Ost} 3} \cdot \mathrm{M}_{\mathrm{P} 2}}{\mathrm{EI}} \mathrm{dS} \\ &\delta_{23}=\frac{1}{\mathrm{EI}}\left[\frac{3}{6} \cdot\left(-2 \cdot 1.2 \cdot \frac{48}{95}+1 \cdot 2 \cdot \frac{36}{19}\right)-\frac{2}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{48}{95}+1.2 \cdot \frac{40}{19}\right)\right]=-\frac{68}{95} \cdot \frac{1}{\mathrm{EI}} \quad \delta_{32}=\delta_{23} \end{aligned} $$ przyjmuję \( \mathrm{m}=100 \mathrm{~kg} \quad \mathrm{~m}_1=1 \mathrm{~m} \quad \mathrm{~m}_2=1 \mathrm{~m} \quad \mathrm{~m}_3=2.5 \mathrm{~m} \)
Szukamy pierwiastków równania
$$ \left|\left(\begin{array}{ccc} \mathrm{m}_1 \cdot \delta_{11}-\frac{1}{\omega^2} & \mathrm{~m}_2 \cdot \delta_{12} & \mathrm{~m}_3 \cdot \delta_{13} \\ \mathrm{~m}_1 \cdot \delta_{21} & \mathrm{~m}_2 \cdot \delta_{22}-\frac{1}{\omega^2} & \mathrm{~m}_3 \cdot \delta_{23} \\ \mathrm{~m}_1 \cdot \delta_{31} & \mathrm{~m}_2 \cdot \delta_{32} & \mathrm{~m}_3 \cdot \delta_{33}-\frac{1}{\omega^2} \end{array}\right)\right|=0 $$ (mnożymy obustronnie przez El/m ) podstawiamy \( \quad \mathrm{x}=\frac{1}{\omega^2} \frac{\mathrm{EI}}{\mathrm{m}} \)\( \left[\begin{array}{ccc} 1 \cdot \frac{77}{76}-x & 1 \cdot\left(-\frac{79}{190}\right) & \frac{5}{2} \cdot \frac{110}{57} \\ 1 \cdot\left(-\frac{79}{190}\right) & 1 \cdot \frac{93}{95}-x & \frac{5}{2}\left(\frac{68}{95}\right) \\ 1 \cdot \frac{110}{57} & 1 \cdot\left(\frac{68}{95}\right) & \frac{5}{2} \cdot \frac{1136}{57}-x \end{array}\right]=0 \)
\( \left[\begin{array}{llc} \frac{77}{76}-\mathrm{x} & -\frac{79}{190} & \frac{275}{57} \\ -\frac{79}{190} & \frac{93}{95}-\mathrm{x} & -\frac{34}{19} \\ \frac{110}{57} & -\frac{68}{95} & \frac{2840}{57}-\mathrm{x} \end{array}\right]=0 \)
Następnie należy metodą Sarrusa obliczyć wyznacznik z powyższej macierzy 3x3 i uprościć go do postaci wielomianu 3-go stopnia (jak poniżej). Najlepiej jeśli mamy do dyspozycji jakiś program, który może nam to uprościć, np. Mathcad.
\( -1 \cdot x^3+51.8167 \cdot x^2-89.4833 \cdot x+33.2632=0 \)
Pierwiastki równania $$ \mathrm{x}_1=0.537 \quad \mathrm{x}_2=1.238 \quad \mathrm{x}_3=50.042 $$ ponieważ \( \mathrm{x}=\frac{1}{\omega^2} \frac{\text { EI }}{\mathrm{m}} \quad \omega=\frac{1}{\sqrt{\mathrm{x}}} \cdot \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}} \)
Częstości drgań własnych
$$ \begin{aligned} &\omega_1=\frac{1}{\sqrt{x_3}}=0.14136 \cdot \sqrt{\frac{\text { EI }}{\mathrm{m}}} \\ &\omega_2=\frac{1}{\sqrt{x_2}}=0.899 \cdot \sqrt{\frac{E I}{\mathrm{~m}}} \\ &\omega_3=\frac{1}{\sqrt{x_1}}=1.3647 \cdot \sqrt{\frac{E I}{\mathrm{~m}}} \end{aligned} $$ Sztywność na zginanie $$ \begin{aligned} &\text { Dla } \quad \mathrm{I}=2140 \cdot 10^{-8} \mathrm{~m}^4 \quad \text { i modułu Younga dla stali } \quad \mathrm{E}=200 \cdot 10^9 \mathrm{~Pa} \\ &\mathrm{EI}=\mathrm{E} \cdot \mathrm{I}=4280000.000 \mathrm{Nm}^2 \quad \mathrm{~m}=100 \quad \mathrm{~kg} \\ &\omega_{1}=0.14136 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}=29.245 \quad \frac{\mathrm{rad}}{\mathrm{s}} \\ &\omega_{2}=0.899 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}=185.939 \frac{\mathrm{rad}}{\mathrm{s}} \\ &\omega_{3}=1.365 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}=282.33 \quad \frac{\mathrm{rad}}{\mathrm{s}} \end{aligned} $$
Wyznaczenie postaci drgań $$ \begin{aligned} &\left(\mathrm{m}_1 \cdot \delta_{11}-\mathrm{x}\right) \cdot \mathrm{A}_{11}+\mathrm{m}_2 \cdot \delta_{12} \cdot \mathrm{A}_{21}+\mathrm{m}_3 \cdot \delta_{13} \cdot \mathrm{A}_{31}=0 \\ &\mathrm{~m}_1 \cdot \delta_{12} \cdot \mathrm{A}_{11}+\left(\mathrm{m}_2 \cdot \delta_{22}-\mathrm{x}\right) \cdot \mathrm{A}_{21}+\mathrm{m}_3 \cdot \delta_{23} \cdot \mathrm{A}_{31}=0 \\ &\mathrm{~m}_1 \cdot \delta_{31} \cdot \mathrm{A}_{11}+\mathrm{m}_2 \cdot \delta_{32} \cdot \mathrm{A}_{21}+\left(\mathrm{m}_3 \cdot \delta_{33}-\mathrm{x}\right) \cdot \mathrm{A}_{31}=0 \end{aligned} $$
Taki układ równań jak powyżej rozwiążemy trzy razy, albowiem raz za "x" podstawimy "x1", raz "x2" i raz "x3".
Po podstawieniu x, mamy układ 3 równań z trzema niewiadomymi A11, A21, A31. Ten układ równań zawsze ma nieskończenie wiele rozwiązań,
musimy więc pokazać jedno przykładowe rozwiązanie. To znaczy założymy za jedną z niewiadomych wartość równą 1, i zostanie nam układ 3 równań z dwoma niewiadomymi, gdzie jak rozwiążemy układ dwóch pierwszych równań to obliczymy pozostałe dwie niewiadome.
dla \( \quad \mathrm{x}=\mathrm{x}_1=0.537 \quad zakładam \quad \mathrm{A}_{11}=1 \)
$$ \begin{aligned} &0.476+0.416 \mathrm{~A}_{21}+4.825 \cdot \mathrm{A}_{31}=0 \\ &-0.416+0.442 \mathrm{~A}_{21}-1.7895 \cdot \mathrm{A}_{31}=0 \\ &1.9298-0.716 \cdot \mathrm{A}_{21}+49.288 \cdot \mathrm{A}_{31}=0 \end{aligned} $$ Rozwiązuję układ dwóch pierwszych równań
$$ \begin{aligned} &\mathrm{A}_{21}=0.831 \\ &\mathrm{~A}_{31}=-0.027 \end{aligned} $$ I postać drgań

dla \( \quad \mathrm{x}=\mathrm{x}_2=1.238 \quad zakładam \quad \mathrm{A}_{12}=1 \)
$$ \begin{aligned} &-0.225-0.416 \cdot \mathrm{A}_{22}+4.825 \cdot \mathrm{A}_{32}=0 \\ &-0.416-0.259 \cdot \mathrm{A}_{22}-1.7895 \cdot \mathrm{A}_{32}=0 \\ &1.9298-0.716 \cdot \mathrm{A}_{22}+48.587 \cdot \mathrm{A}_{32}=0 \end{aligned} $$ Rozwiązuję układ dwóch pierwszych równań
$$ \begin{aligned} &\mathrm{A}_{22}=-1.208 \\ &\mathrm{~A}_{32}=-0.0575 \end{aligned} $$ II postać drgań

dla \( \quad \mathrm{x}=\mathrm{x}_3=50.042 \quad zakładam \quad \mathrm{A}_{13}=1 \)
$$ \begin{gathered} -49.0286-0.416 \cdot \mathrm{A}_{23}+4.825 \cdot \mathrm{A}_{33}=0 \\ -0.416-49.063 \cdot \mathrm{A}_{23}-1.7895 \cdot \mathrm{A}_{33}=0 \\ 1.9298-0.716 \cdot \mathrm{A}_{23}-0.217 \cdot \mathrm{A}_{33}=0 \end{gathered} $$ Rozwiązuję układ dwóch pierwszych równań
$$ \begin{aligned} &\mathrm{A}_{23}=-0.378 \\ &\mathrm{~A}_{33}=10.130 \end{aligned} $$ III postać drgań

Sprawdzenie warunków ortogonalności
\begin{aligned} &\mathrm{m}_1 \cdot \mathrm{A}_{11} \cdot \mathrm{A}_{12}+\mathrm{m}_2 \cdot \mathrm{A}_{21} \cdot \mathrm{A}_{22}+\mathrm{m}_3 \cdot \mathrm{A}_{31} \cdot \mathrm{A}_{32}=0 \\ &\mathrm{~m}_1 \cdot \mathrm{A}_{12} \cdot \mathrm{A}_{13}+\mathrm{m}_2 \cdot \mathrm{A}_{22} \cdot \mathrm{A}_{23}+\mathrm{m}_3 \cdot \mathrm{A}_{32} \cdot \mathrm{A}_{33}=0 \\ &\mathrm{~m}_1 \cdot \mathrm{A}_{11} \cdot \mathrm{A}_{13}+\mathrm{m}_2 \cdot \mathrm{A}_{21} \cdot \mathrm{A}_{23}+\mathrm{m}_3 \cdot \mathrm{A}_{31} \cdot \mathrm{A}_{33}=0 \\ \end{aligned}
\begin{aligned} &1 \cdot 1 \cdot \mathrm{m}+1 \mathrm{~m} \cdot 0.831 \cdot(-1.208)+2.5 \mathrm{~m} \cdot(-0.027) \cdot(-0.0575) \rightarrow 0.00003 \mathrm{~m} \sim 0 \\ &1 \cdot 1 \cdot \mathrm{m}+1 \mathrm{~m} \cdot 0.831 \cdot(-1.208)+2.5 \mathrm{~m} \cdot(-0.027) \cdot(-0.0575) \rightarrow 0.00003 \mathrm{~m} \sim 0 \\ &1 \cdot 1 \cdot \mathrm{m}+1 \mathrm{~m} \cdot 0.831 \cdot(-0.378)+2.5 \mathrm{~m} \cdot(-0.027) \cdot 10.1297 \rightarrow 0.00213 \mathrm{~m} \sim 0 \end{aligned}
sprawdzenie daje pozytywny wynik
Jeżeli masz jakieś pytania, uwagi lub wydaje Ci się, że znalazłeś błąd w tym rozwiązaniu, napisz proszę do nas wiadomość na kontakt@edupanda.pl lub skontaktuj się z nami przez nasz profil na FB:
