Przed rozpoczęciem tego przykładu zachęcamy do zapoznania się z krótkim wstępem teoretycznym na poprzedniej stronie.

Obliczamy reakcje podporowe i rysujemy wykres momentów. Następnie zamieniamy belkę rzeczywistą na belkę fikcyjną i odpowiednio ją obciążamy.

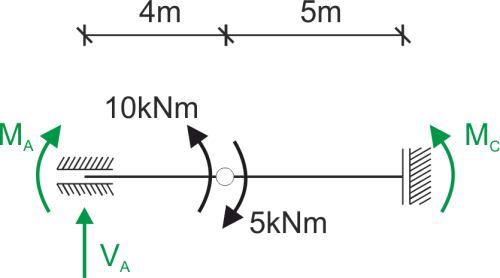\begin{aligned} &\sum M_B^P=0\\ &5-M_C=0\ \Rightarrow M_C=5\ kNm\\ &\sum M_B^L=0\\ &M_A-10=0\ \Rightarrow M_A=10\ kNm\\ &\sum y=0\\ &V_A=0\\ \end{aligned}

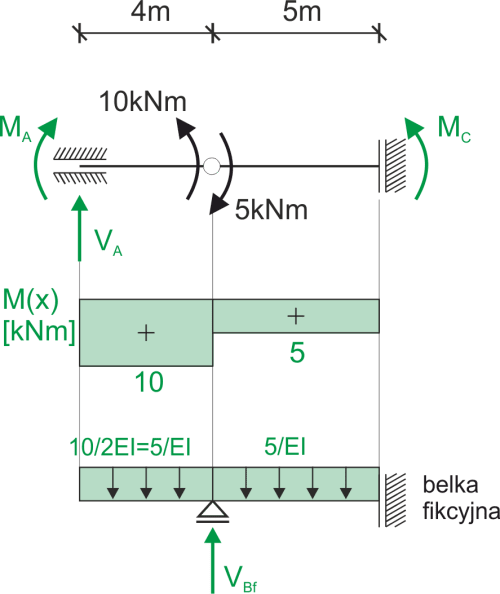
Belka fikcyjna

\begin{aligned} &\sum y=0\\ &V_{Bf}-\frac{5}{EI}\cdot 9=0\\ &V_{Bf}=\frac{45}{EI}\\ \\ &w_B=M_{fB}=-\frac{5}{EI}\cdot 4\cdot 2=-\frac{40}{EI}\\ &w_C=M_{fC}=-\frac{5}{EI}\cdot 9\cdot 4,5+\frac{45}{EI}\cdot 5=\frac{22,5}{EI}\\ \end{aligned}

Charakterystyki przekroju, sztywność na zginanie EI

\begin{aligned} &E=200 GPa\\ &I=\frac{0,15\cdot 0,2^3}{12}=1\cdot 10^{-4}\ m^4\\ &EI=(200\cdot 10^9\cdot 1\cdot 10^{-4})\cdot 10^{-3}=20 000\ kNm^2\\ \end{aligned}

Liczymy szukane przemieszczenia

\begin{aligned} &w_B=-\frac{40}{20 000}=-2\ mm\\ &w_C=\frac{22,5}{20000}=1,125\ mm\\ \end{aligned}