Rozwiązanie
Zachęcamy do obejrzenia rozwiązania tego przykładu (i innych) na naszym kanale YouTube. Wyjaśniamy krok po kroku, jak rozwiązać to zadanie. Obejrzenie tego materiału pomoże Ci również zrozumieć inne przykłady na naszej stronie.
\begin{aligned}\\ &Q(x)=-30+15x\\ &Q(x=0)=-30\ kN\\ &Q(x=6)=60\ kN\\ &Ekstremum \\ &Q(x)=-30+15x=0\\ &x=2[m]\\ &M(x=0)=30\cdot 6-\frac{1}{2}\cdot 15\cdot 6^2=-90\ kNm\\ &M_{max}(x-2)=30\ kNm\\ &M(x=6)=30\cdot 6-\frac{1}{2}\cdot 15\cdot 6^2=-90\ kNm\\ \end{aligned}Wykres sił poprzecznych i momentów zginających
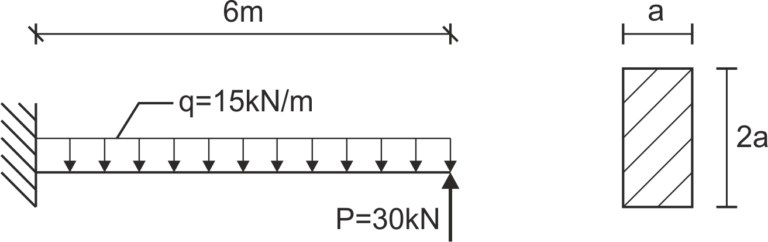
Wymiarowanie
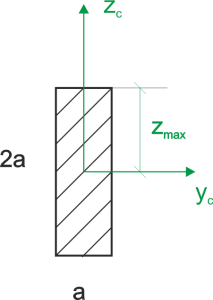 \begin{aligned}\\ &I_{y_c}=\frac{b*h^3}{12}=\frac{a*(2a)^3}{12}=\frac{2}{3}a^4 \\ &W=\frac{I_{y_c}}{z_{max}}=\frac{\frac{2}{3}a^4}{a}=\frac{2}{3}a^3\\ \end{aligned}
\begin{aligned}\\ &I_{y_c}=\frac{b*h^3}{12}=\frac{a*(2a)^3}{12}=\frac{2}{3}a^4 \\ &W=\frac{I_{y_c}}{z_{max}}=\frac{\frac{2}{3}a^4}{a}=\frac{2}{3}a^3\\ \end{aligned}
Warunek wytrzymałościowy
\begin{aligned}\\ &|\frac{M_{max}}{W}|\le k_g\\ &\frac{90*10^3}{\frac{2}{3}a^3}\le 160*10^6\\ &a\ge 0,09449 \ m\\ & a=95\ mm\\ \end{aligned}Naprężenia
\begin{aligned}\\ &\sigma=\frac{M}{W}=\frac{90*10^3}{\frac{2}{3}*(0,095)^3}=157,46 \ MPa\\ \end{aligned}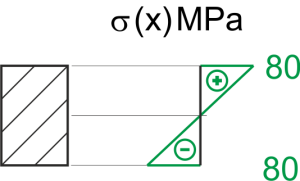
Jeżeli masz jakieś pytania, uwagi lub wydaje Ci się, że znalazłeś błąd w tym rozwiązaniu, napisz proszę do nas wiadomość na kontakt@edupanda.pl lub skontaktuj się z nami przez nasz profil na FB:
