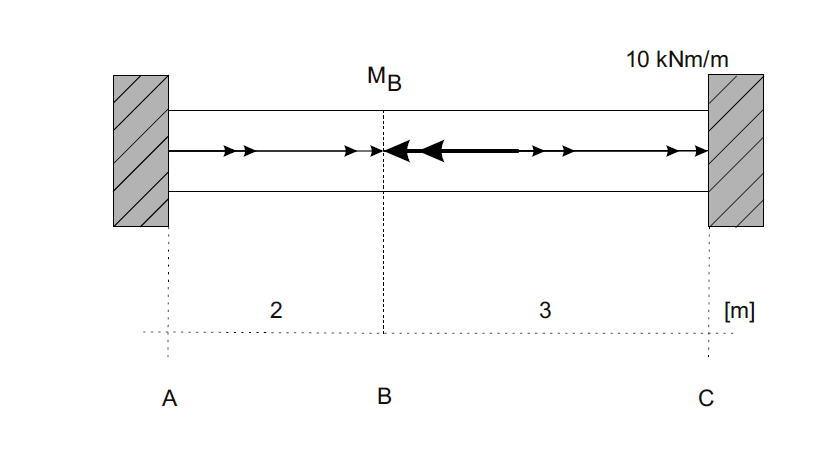
Task content

A rod with a circular cross-section with a diameter of \(d = 10 \text{ cm}\) is made of a material with a shear modulus of \(G = 101,80 \text{ GPa}\). Calculate the moment of inertia for the torsion of the cross-section: \(J_s\) in \([\text{cm}^4]\).

For a doubly supported rod, loaded along its entire length with a uniformly distributed moment of intensity \(10 \text{ kNm/m}\) and a concentrated moment in the cross-section \(B\) with a value of \(M_0 = 30 \text{ kNm}\), acting opposite to the distributed moment, draw the graphs:

\(M_s\) - torsional moments - section forces and describe in \([\text{kNm}]\).

\(\varphi\) - angles of rotation relative to the support and describe in \([10^{-3} \text{ rad}]\).

Note: describe the extrema - that is, indicate on the drawing where they will occur and what their values will be. Calculate the maximum value of shear stress in this rod: \(\tau_{\text{max}}\) \([\text{MPa}]\).