Linie wpływu - wprowadzenie

Z tego artykułu dowiesz się, czym są linie wpływu, jak je prawidłowo interpretować oraz poznasz podstawowe metody ich wyznaczania.

Czym jest linia wpływu?

Linia wpływu (lub linia wpływowa) to wykres, który w sposób graficzny pokazuje, jak zmienia się wartość konkretnej wielkości statycznej (np. reakcji podporowej, siły tnącej lub momentu gnącego) w jednym, ustalonym punkcie konstrukcji, w zależności od położenia ruchomej, jednostkowej siły (P=1), która przemieszcza się po tej konstrukcji.

Można to sobie wyobrazić jako śledzenie, jak zmienia się np. siła nacisku na filar mostu, gdy przejeżdża po nim pojedynczy, wzorcowy pojazd. Linia wpływu jest właśnie zapisem tych zmian.

Do czego służą linie wpływu?

Głównym celem stosowania linii wpływu jest znalezienie najniekorzystniejszego położenia obciążenia dla danej konstrukcji. Jest to fundamentalne narzędzie w projektowaniu, szczególnie mostów, belek podsuwnicowych i innych konstrukcji poddanych działaniu obciążeń ruchomych.

Dzięki nim projektant może odpowiedzieć na kluczowe pytania:

• Gdzie należy ustawić ciężki pojazd na moście, aby wywołać maksymalny moment gnący w jego środku?
• Jak rozmieścić obciążenie, by reakcja na jednej z podpór była największa?
• W którym miejscu obciążenie ruchome spowoduje maksymalną siłę tnącą w danym przekroju?

Znalezienie tych ekstremalnych wartości sił i momentów jest niezbędne do prawidłowego i bezpiecznego zwymiarowania konstrukcji.

Jak interpretować wykres linii wpływu?

Interpretacja wykresu linii wpływu wymaga zrozumienia, co reprezentują jego osie:

• Oś pozioma (oś odciętych, x): Reprezentuje położenie ruchomej siły jednostkowej P=1 na konstrukcji.
• Oś pionowa (oś rzędnych, y): To rzędna linii wpływu. Jej wartość pokazuje, ile wynosi badana wielkość (np. reakcja V_A, moment M_k) w stałym, analizowanym punkcie, gdy siła P=1 znajduje się dokładnie nad tą rzędną.

Przykład: Jeśli rzędna linii wpływu reakcji V_A w punkcie "x" wynosi 0.5, oznacza to, że gdy siła P=1 jest przyłożona w punkcie "x", to reakcja na podporze A wynosi V_A = 0.5. Gdyby w tym miejscu działała rzeczywista siła P = 100 kN, reakcja wyniosłaby V_A = 0.5 * 100 kN = 50 kN.

Fundamentalny przypadek linii wpływu

Rysunki ilustrują najprostszy, a zarazem fundamentalny przypadek: reakcji podporowych oraz sił przekrojowych dla belki swobodnie podpartej.

Linia wpływu reakcji lewej podpory (V_A)

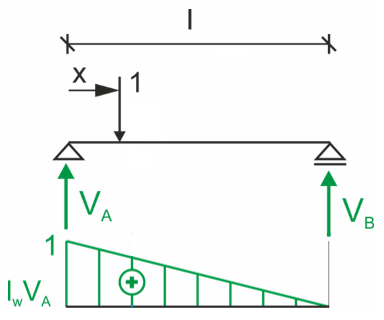
Wykres ten obrazuje, jak siła P=1, przesuwając się po belce, wpływa na wartość reakcji na podporze A. Kształt linii wpływu to trójkąt prostokątny:

• Gdy siła P=1 jest nad podporą A (x=0), to ta podpora przejmuje całe obciążenie, a rzędna linii wpływu ma wartość 1.
• W miarę przesuwania siły w prawo, reakcja w A maleje liniowo.
• Gdy siła P=1 dociera nad podporę B (x=l), podpora A nie przenosi już żadnego obciążenia, a rzędna linii wpływu wynosi 0.

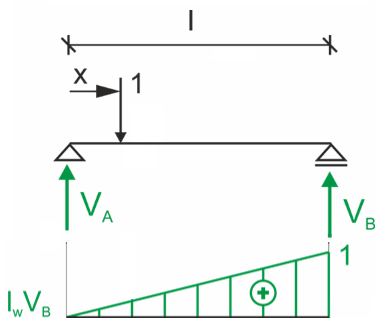
Linia wpływu reakcji prawej podpory (V_B)

Gdy siła P=1 jest nad podporą A (x=0), podpora B nie jest obciążona, więc rzędna linii wpływu ma wartość 0.

W miarę przesuwania siły w prawo, reakcja w B rośnie liniowo.

Gdy siła P=1 dociera nad podporę B (x=l), to ta podpora przejmuje całe obciążenie, a rzędna linii wpływu osiąga wartość 1.

Linia wpływu siły tnącej w przekroju "k"

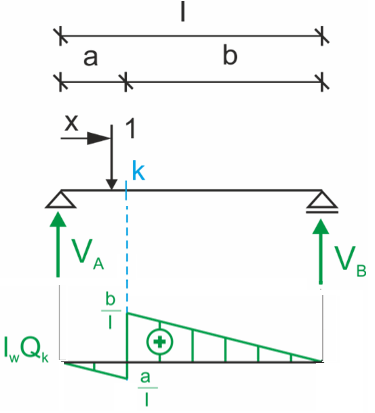
Linia wpływu siły tnącej w ustalonym przekroju "k" (w odległości `a` od lewej podpory) jest bardziej złożona. Składa się z dwóch trójkątów i charakteryzuje się "skokiem" (nieciągłością) o wartości 1 dokładnie w miejscu analizowanego przekroju.

Ten charakterystyczny skok pokazuje, że największe (co do wartości bezwzględnej) siły tnące w przekroju "k" występują, gdy obciążenie skupione znajduje się tuż przy tym przekroju.

Linia wpływu momentu gnącego w przekroju "k"

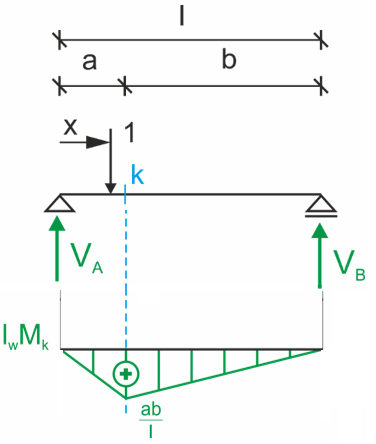
Linia wpływu momentu gnącego w przekroju "k" ma kształt pojedynczego trójkąta (namiotu) i w przeciwieństwie do siły tnącej, jest funkcją ciągłą.

Z tego wykresu jednoznacznie wynika, że aby wywołać maksymalny moment gnący w danym punkcie belki, należy obciążenie skupione umieścić dokładnie w tym punkcie.

W dalszej części tekstu znajdziesz wyprowadzenie analityczne w formie kursu wideo dla wyżej zaprezentowanego przykładu belki prostej wolnopodpartej.

Na dole strony w sekcji ZOBACZ TEŻ znajdziesz odnosnik do zadań z belek prostych - trzy pierwsze przypadki prezentują belki podstawowe, dla pierwszej wyprowadzenie analityczne linii wpływu jest w tym tekście, a dla dwóch pozostałych wyprowadzenie w formie kursu wideo znajdziesz w przykładzie 2 oraz 3.

Podstawowe metody wyznaczania linii wpływu

Istnieją dwie główne metody wyznaczania linii wpływu:

• Metoda analityczna (statyczna):
  • Polega na zapisaniu klasycznych równań równowagi statycznej.
  • Siłę jednostkową P=1 umieszcza się w dowolnym miejscu, opisanym zmienną "x".
  • Z równań równowagi wyznacza się wzór na poszukiwaną wielkość (np. reakcję) jako funkcję zmiennej "x".
  • Otrzymany wzór (zawsze będzie to funkcja liniowa dla układów statycznie wyznaczalnych) jest następnie wykreślany.
• Metoda kinematyczna (z zasady prac wirtualnych):
  • Szybsza, graficzna metoda oparta na zasadzie prac wirtualnych.
  • W miejscu badanej wielkości (np. w przekroju, w którym szukamy momentu) wprowadzamy "kinematyczne uwolnienie więzi" (np. przegub) i nadajemy jednostkowe przemieszczenie (np. jednostkowy obrót).
  • Kształt, jaki przyjmie odkształcona w ten sposób konstrukcja, jest (z dokładnością do stałej) kształtem szukanej linii wpływu. Ta metoda jest niezwykle efektywna, zwłaszcza przy bardziej skomplikowanych układach, jak kratownice czy ramy.