Metoda sił

Wprowadzenie do Metody Sił

W mechanice budowli konstrukcje dzielimy na dwie podstawowe kategorie: statycznie wyznaczalne i statycznie niewyznaczalne (hiperstatyczne). Układy statycznie wyznaczalne można w pełni przeanalizować za pomocą samych równań równowagi statycznej. Jednak większość rzeczywistych konstrukcji inżynierskich, takich jak wieloprzęsłowe belki, ramy portalowe czy złożone kratownice, to układy statycznie niewyznaczalne. Oznacza to, że posiadają one więcej więzi (reakcji podporowych, połączeń) niż jest to absolutnie konieczne do zapewnienia ich niezmienności geometrycznej, co prowadzi do większej liczby niewiadomych niż dostępnych równań równowagi.

Do rozwiązania tego problemu służą zaawansowane metody, a jedną z najbardziej klasycznych i fundamentalnych jest metoda sił. Pozwala ona w usystematyzowany sposób rozwiązywać układy hiperstatyczne, sprowadzając je do analizy prostszych, znanych już układów statycznie wyznaczalnych.

Podstawowa idea i kluczowe pojęcia

Główna idea metody sił polega na myślowym przekształceniu układu statycznie niewyznaczalnego w układ statycznie wyznaczalny poprzez usunięcie "nadliczbowych" więzi. Te usunięte więzi zastępujemy niewiadomymi siłami, które nazywamy siłami nadliczbowymi lub hiperstatycznymi, oznaczanymi najczęściej jako \(X_i\).

W ten sposób otrzymujemy tzw. układ podstawowy – jest to konstrukcja statycznie wyznaczalna, obciążona zarówno siłami zewnętrznymi, jak i niewiadomymi siłami nadliczbowymi \(X_i\). Kluczem do rozwiązania zadania jest znalezienie wartości tych sił nadliczbowych. Przyjęty układ podstawowy oczywiście musi być geometrycznie niezmienny, więc nie jest bez znaczenia które więzi usuniemy. Poniżej przykładowy temat ramy dwukrotnie statycznie niewyznaczalnej oraz przyjęte układy podstawowe - jeden z nich jest błędny.

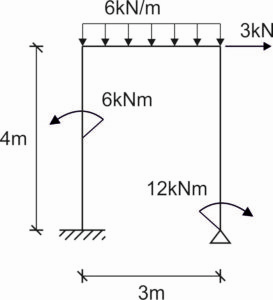
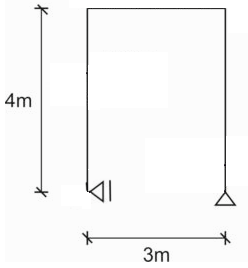
Na rysunku 3 kierunki wszystkich reakcji przecinają się w jednym punkcie, co oznacza, że układ podstawowy jest geometrycznie zmienny (chwiejny).

Równania kanoniczne metody sił

Wartości sił nadliczbowych \(X_i\) wyznaczamy, korzystając z warunków zgodności przemieszczeń. Warunki te mówią, że przemieszczenie w miejscu usuniętej więzi, obliczone w układzie podstawowym, musi być równe zeru (lub innej znanej wartości, np. w przypadku osiadania podpory). Innymi słowy, odtwarzamy pierwotne, rzeczywiste warunki geometryczne konstrukcji.

Opierając się na zasadzie superpozycji, możemy stwierdzić, że całkowite przemieszczenie w kierunku działania siły \(X_i\) jest sumą przemieszczeń od:

• Działania obciążeń zewnętrznych (\(P\)) na układzie podstawowym.
• Działania każdej z poszczególnych sił nadliczbowych \(X_k\).

Prowadzi to do sformułowania układu równań algebraicznych, zwanych równaniami kanonicznymi metody sił. Dla układu o \(n\)-krotnej statycznej niewyznaczalności, układ ten ma postać:

\[ \begin{cases} \delta_{11}X_1 + \delta_{12}X_2 + \dots + \delta_{1n}X_n + \Delta_{1P} = 0 \\ \delta_{21}X_1 + \delta_{22}X_2 + \dots + \delta_{2n}X_n + \Delta_{2P} = 0 \\ \vdots \\ \delta_{n1}X_1 + \delta_{n2}X_2 + \dots + \delta_{nn}X_n + \Delta_{nP} = 0 \end{cases} \]

Poszczególne współczynniki w tych równaniach oznaczają:

• \(X_1, X_2, \dots, X_n\) – niewiadome wartości sił nadliczbowych.
• \(\delta_{ik}\) – tzw. przemieszczenie jednostkowe; jest to przemieszczenie w układzie podstawowym w kierunku siły \(X_i\), wywołane działaniem siły jednostkowej \(X_k=1\).
• \(\Delta_{iP}\) – tzw. wyraz wolny; jest to przemieszczenie w układzie podstawowym w kierunku siły \(X_i\), wywołane działaniem rzeczywistych obciążeń zewnętrznych \(P\).

Wszystkie współczynniki \(\delta_{ik}\) oraz \(\Delta_{iP}\) obliczane są jako przemieszczenia w układzie statycznie wyznaczalnym, najczęściej przy użyciu wzoru całkowego Maxwella-Mohra (najczęściej upraszczanych graficznie regułą Wiereszczagina).

Algorytm postępowania w metodzie sił

Rozwiązanie zadania metodą sił przebiega w kilku usystematyzowanych krokach:

1. Określenie stopnia statycznej niewyznaczalności (\(n\)) konstrukcji.
2. Wybór układu podstawowego poprzez usunięcie \(n\) więzi i wprowadzenie w ich miejsce niewiadomych sił nadliczbowych \(X_1, X_2, \dots, X_n\).
3. Zapisanie układu równań kanonicznych dla wybranego układu podstawowego.
4. Narysowanie wykresów momentów gnących od obciążeń zewnętrznych i sił nadliczbowych.
5. Obliczenie współczynników \(\delta_{ik}\) i wyrazów wolnych \(\Delta_{iP}\) za pomocą całek Maxwella-Mohra (często upraszczanych graficznie regułą Wereszczagina).
6. Rozwiązanie układu równań i obliczenie wartości niewiadomych sił nadliczbowych \(X_i\).
7. Wyznaczenie ostatecznych sił wewnętrznych (i reakcji) w układzie statycznie niewyznaczalnym poprzez superpozycję wyników z układu podstawowego, zgodnie ze wzorem:
   \( S_{ost} = S_P + \sum_{i=1}^{n} X_i \cdot s_i \)
   gdzie \(S_{ost}\) to ostateczna siła wewnętrzna (np. moment), \(S_P\) to siła wewnętrzna od obciążeń zewnętrznych w układzie podstawowym, a \(s_i\) to siła wewnętrzna od działania siły jednostkowej \(X_i=1\).

Metoda sił jest potężnym i uniwersalnym narzędziem, które porządkuje analizę skomplikowanych konstrukcji, stanowiąc fundament dla wielu nowoczesnych technik obliczeniowych, w tym Metody Elementów Skończonych (MES).