Ramy przestrzenne

Ramy przestrzenne – Wprowadzenie do analizy trójwymiarowej

Po analizie układów płaskich (belek, ram) i rusztów, naturalnym krokiem jest przejście do ram przestrzennych. Są to najbardziej ogólne układy prętowe, w których osie prętów oraz działające obciążenia mogą być dowolnie zorientowane w przestrzeni trójwymiarowej. Ta swoboda geometryczna sprawia, że analiza ram przestrzennych jest znacznie bardziej złożona niż w przypadku układów 2D, ponieważ w każdym przekroju musimy uwzględnić aż sześć, a nie trzy, składowe sił wewnętrznych.

Ramy przestrzenne stanowią szkielet wielu zaawansowanych konstrukcji inżynierskich, takich jak wieże, maszty, szkielety budynków wysokich, konstrukcje wsporcze w przemyśle czy złożone systemy dachowe.

Siły wewnętrzne w ramie przestrzennej

W przeciwieństwie do układu płaskiego, w którym występowały trzy siły wewnętrzne, myślowe przecięcie pręta w układzie przestrzennym ujawnia sześć składowych sił wewnętrznych, odpowiadających sześciu stopniom swobody ciała w przestrzeni:

• Siła osiowa (\(N_x\)): Działająca wzdłuż osi pręta.
• Dwie siły tnące (\(Q_y, Q_z\)): Działające w płaszczyźnie przekroju, prostopadle do osi pręta.
• Moment skręcający (\(M_s\), lub \(M_x\)): Skręcający pręt wokół jego osi podłużnej.
• Dwa momenty gnące (\(M_y, M_z\)): Zginające pręt wokół dwóch głównych osi bezwładności przekroju.

Ta złożoność sprawia, że zarówno określenie stanu wytężenia, jak i obliczenie przemieszczeń wymaga znacznie bardziej rozbudowanego aparatu matematycznego.

Geometryczna niezmienność układów przestrzennych

Zanim przystąpimy do jakiejkolwiek analizy statycznej, musimy upewnić się, że rama jest geometrycznie niezmienna. Ciało sztywne w przestrzeni ma sześć stopni swobody (trzy translacje i trzy obroty). Aby je unieruchomić, potrzebujemy co najmniej sześciu elementarnych więzów (składowych reakcji).

Jednak sama liczba więzów nie wystarczy. Kluczowe jest ich prawidłowe rozmieszczenie geometryczne. Układ jest chwiejny (geometrycznie zmienny), jeśli więzy są rozmieszczone w sposób wadliwy. Dla sztywnej bryły podpartej sześcioma prętami, ogólny warunek niezmienności mówi, że osie prętów podporowych nie mogą przecinać jednej prostej. Z tego wynikają następujące, bardziej praktyczne warunki, które muszą być spełnione:

• Pręty podporowe nie mogą leżeć w jednej płaszczyźnie (ani w dwóch płaszczyznach).
• Co najwyżej trzy pręty mogą być do siebie równoległe.
• Co najwyżej trzy pręty mogą przecinać się w jednym punkcie.
• Krawędź przecięcia się dwóch płaszczyzn, w których leży pięć prętów, nie może być równoległa do szóstego pręta (ten warunek zapobiega rotacji wokół tej krawędzi).

Niespełnienie któregokolwiek z tych warunków prowadzi do powstania mechanizmu i utraty stabilności konstrukcji.

Bardzo często ramy przestrzenne są podparte wspornikowo - oczywiście takie podparcie zapewnia geometryczną niezmienność

Stopień statycznej niewyznaczalności i układ podstawowy

Ramy przestrzenne mogą być statycznie wyznaczalne lub niewyznaczalne. Do określenia stopnia statycznej niewyznaczalności stosuje się wzór:

\[ n = 6 \cdot p + r - 6 \]

Gdzie: \(p\) – liczba zamkniętych "oczek" (obwodów zamkniętych), \(r\) – liczba reakcji podporowych.

Jeśli rama jest wspornikowa i dodatkowo podparta, to najlepszym układem podstawowym jest zostawienie wspornika i zabranie wszystkich pozostałych więzi

Jeśli rama jest podparta w bardziej złożony sposób, to należy pilnować, aby przyjęty układ podstawowy zapewniał geometryczną niezmienność (patrz wcześniej warunki geometrycznej niezmienności).

Dla powyższej ramy można przyjąć następujący układ podstawowy metody sił:

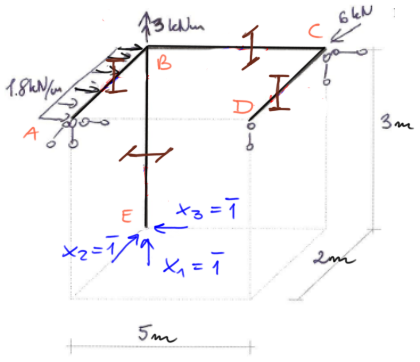
Rozwiązywanie ram przestrzennych metodą sił

Zasada rozwiązywania ram przestrzennych metodą sił jest analogiczna do tej dla układów płaskich i rusztów. Po określeniu stopnia statycznej niewyznaczalności (\(n\)) i wyborze układu podstawowego, zapisujemy układ równań kanonicznych:

\[ \begin{cases} \delta_{11}X_1 + \delta_{12}X_2 + \dots + \delta_{1n}X_n + \Delta_{1P} = 0 \\ \delta_{21}X_1 + \delta_{22}X_2 + \dots + \delta_{2n}X_n + \Delta_{2P} = 0 \\ \vdots \\ \delta_{n1}X_1 + \delta_{n2}X_2 + \dots + \delta_{nn}X_n + \Delta_{nP} = 0 \end{cases} \]

Kluczowa różnica polega na sposobie obliczania współczynników \(\delta_{ik}\) oraz wyrazów wolnych \(\Delta_{iP}\). W układzie przestrzennym musimy uwzględnić energię odkształcenia pochodzącą od wszystkich sześciu sił wewnętrznych (w praktyce wystarczy przecałkować tylko wykresy momentów gnących i skręcających).

\[ \delta = \int_L \frac{M_y(x)\bar{M}_y(x)}{EI_y} dx + \int_L \frac{M_z(x)\bar{M}_z(x)}{EI_z} dx + \int_L \frac{M_s(x)\bar{M}_s(x)}{GI_s} dx \]

Gdzie poszczególne symbole oznaczają:

• \(M_y(x), M_z(x)\) – momenty gnące wokół osi Y i Z w stanie rzeczywistym.
• \(\bar{M}_y(x), \bar{M}_z(x)\) – momenty gnące wokół osi Y i Z w stanie wirtualnym.
• \(M_s(x), \bar{M}_s(x)\) – momenty skręcające w stanie rzeczywistym i wirtualnym.
• \(EI_y, EI_z\) – sztywności giętne przekroju względem odpowiednich osi.
• \(GI_s\) – sztywność na skręcanie, gdzie \(G\) to moduł Kirchhoffa (moduł sprężystości poprzecznej), a \(I_s\) to wskaźnik sztywności na skręcanie.