Wytrzymałość materiałów
Metoda Mohra
- Wprowadzenie do metody Mohra
- Definicja i nazwy alternatywne
- Podejście dwuetapowe
- Belka zastępcza (wtórna, fikcyjna)
- Zasada działania metody
- Algorytm metody Mohra
- Wyznaczanie wykresu momentów zginających
- Określenie belki fikcyjnej
- Obciążenie belki fikcyjnej
- Zwroty obciążenia fikcyjnego
- Znakowanie sił wewnętrznych
- Interpretacja wyników
- Siła tnąca - kąt obrotu
- Moment gnący - ugięcie
- Układ odniesienia
- Znakowanie przemieszczeń
- Zamiana belki rzeczywistej na belkę fikcyjną
- Tabela zamiany podpór
- Zasady transformacji
- Zakres materiału kursu
- Metoda Mohra (grafoanalityczna)
- Projektowanie na ugięcie
- Warunek użytkowalności
- Dopuszczalne obciążenia
- Przykłady obliczeniowe
- Przykład 1 - Zamiana podpór
- Przykład 2 - Wpływ temperatury
- Przykład 3 - Wideo kurs
Wprowadzenie do metody Mohra
Metoda Mohra, znana również jako metoda grafo-analityczna, metoda belki zastępczej, metoda obciążenia wtórnego lub metoda graficzna, opiera się na dwuetapowym podejściu do rozwiązania problemu określenia rozkładu momentów zginających w belce.
W pierwszym kroku zajmujemy się standardowym rozkładem sił przekrojowych w konkretnej (zadanej) belce. Następnie, w drugim etapie, koncentrujemy się na ustaleniu rozkładu momentów w tzw. "belce zastępczej".
Dla belki zastępczej (wtórnej, fikcyjnej) dobieramy geometrię, podparcie i obciążenie w taki sposób, aby, opierając się na rozwiązaniu pierwszego etapu, uzyskać rozkład momentów, który jest liczbowo identyczny z rozkładem ugięć w rzeczywistej belce.
Żeby lepiej zrozumieć zobacz poniższy przykład.
Algorytm metody Mohra
Tok postępowania przy rozwiązaniu zadania
- wyznaczyć wykres momentów zginających w belce rzeczywistej (przyjmując spody na dole belki),
- wyznaczyć belkę fikcyjną/wtórną (zgodnie z tabelą poniżej),
- obciążyć belkę fikcyjną/wtórną wykresem momentów zginających z belki rzeczywistej podzielonemu przez jej sztywność na zginanie EI.
Dodatniemu wykresowi momentów odpowiadają zwroty obciążenia fikcyjnego zgodnego ze zwrotem osi ugięć belki rzeczywistej. To znaczy, jeśli jako dodatnie ugięcie zakładamy przemieszczenie w dół, wówczas dodatni wykres momentu musimy zmienić na obciążenie ciągłe skierowane (zwrot) w dół.

- wyznaczyć siłę poprzeczną i/lub moment zginający w tym wybranym punkcie w belce fikcyjnej, znakowanie:

Interpretacja wyników
Będą one równe odpowiednim przemieszczeniom w tym samym punkcie osi belki rzeczywistej.
Siła tnąca - kąt obrotu
Sile tnącej w punkcie K na belce fikcyjnej odpowiada kąt obrotu punktu K belki rzeczywistej:
\[ \varphi(x)=Q_f (x) \]Moment gnący - ugięcie
Momentowi gnącemu w punkcie K na belce fikcyjnej odpowiada ugięcie belki rzeczywistej w tym punkcie:
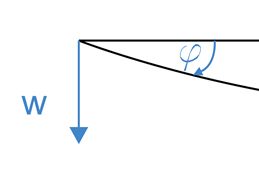
\[ w(x)=M_f (x) \]W przyjętym układzie odniesienia ugięcie w>0 jest skierowane w dół belki, a dodatni kąt obrotu \(\varphi>0\) będzie zgodny z ruchem wskazówek zegara.
Zamiana belki rzeczywistej na belkę fikcyjną
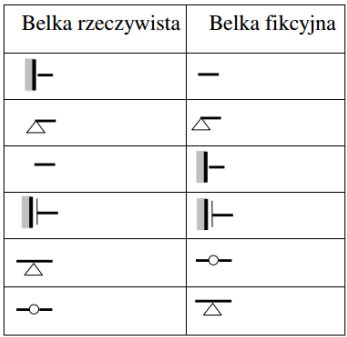
Z tego kursu dowiesz się:
Metoda Mohra (grafoanalityczna):
- jak wyznaczyć wykres momentów gnących,
- jak określić podparcie belki fikcyjnej (wtórnej),
- jak obciążyć belkę wtórną,
- jak obliczyć ugięcie i kąt obrotu belki w dowolnym punkcie.
Projektowanie na ugięcie:
- jak zwymiarować przekrój belki z warunku użytkowalności (na dopuszczalne ugięcie),
- jak wyznaczyć wartość dopuszczalnego obciążenia mając zadany przekrój.
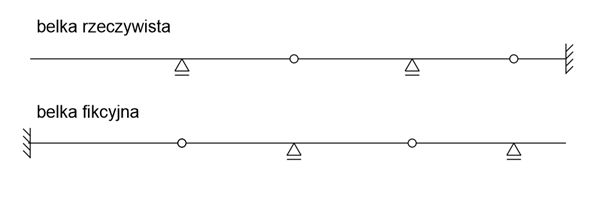
Przykład 1 - Metoda Mohra - zamiana podpór z belki pierwotnej na wtórną
Rozwiązanie
Przykład 2 - Metoda Mohra - wpływ temperatury
Rozwiązanie
Oczywiście metodą Mohra można również obliczyć przemieszczenie od wpływu temperatury. Korzystamy ze wzoru:
\[ \kappa=\frac{\alpha \Delta T}{h} \]Wówczas obciążenie belki fikcyjnej ma wartość κ i jest skierowane w stronę włókien cieplejszych.