Nośność graniczna

Wprowadzenie do nośności granicznej

Analiza nośności granicznej to dział wytrzymałości materiałów, który wykracza poza tradycyjne obliczenia w zakresie sprężystym. Jego celem jest określenie rzeczywistej, maksymalnej zdolności konstrukcji do przenoszenia obciążeń, aż do momentu, w którym przekształca się ona w mechanizm i ulega zniszczeniu. Jest to kluczowe zagadnienie w nowoczesnym projektowaniu, pozwalające na wykorzystanie tzw. rezerw plastycznych materiału i bardziej ekonomiczne wymiarowanie, zwłaszcza w przypadku konstrukcji statycznie niewyznaczalnych.

Model materiału – Ciało idealnie sprężysto-plastyczne

Podstawą teorii nośności granicznej jest uproszczony model materiału, znany jako ciało idealnie sprężysto-plastyczne (model Prandtla). Zakłada on, że materiał (np. stal) początkowo zachowuje się liniowo-sprężyście (zgodnie z prawem Hooke'a), a po osiągnięciu granicy plastyczności (\(R_e\)) odkształca się dalej przy stałym naprężeniu, bez wzmocnienia. Taka idealizacja doskonale oddaje zachowanie stali z wyraźną granicą plastyczności i jest fundamentem całej teorii.

Fazy pracy przekroju zginanego – Od sprężystości do plastyczności

Aby zrozumieć nośność całej konstrukcji, musimy najpierw przeanalizować, co dzieje się w pojedynczym przekroju pod wpływem rosnącego momentu zginającego. Wyróżniamy cztery kluczowe stany pracy:

1. Stan sprężysty: Przy niewielkich obciążeniach naprężenia w przekroju rozkładają się liniowo, osiągając maksymalną wartość w skrajnych włóknach. Rozkład ten jest antysymetryczny względem osi obojętnej, która przechodzi przez środek ciężkości przekroju sprężystego.
2. Graniczny stan sprężysty: Moment zginający osiąga wartość, przy której naprężenia w skrajnych włóknach dochodzą do granicy plastyczności (\(R_e\)). Moment ten nazywamy granicznym momentem sprężystym (\(M_{el}\)).
3. Stan sprężysto-plastyczny: Dalsze zwiększanie momentu powoduje, że strefy uplastycznienia "wędrują" od skrajnych włókien w głąb przekroju. W przekroju współistnieją obszary plastyczne i sprężysty rdzeń.
4. Graniczny stan plastyczny: Cały przekrój ulega uplastycznieniu. Oś obojętna przesuwa się do tzw. osi plastycznej, która dzieli przekrój na dwie części o równych polach. Moment, który wywołuje ten stan, to graniczny moment plastyczny (\(M_{pl}\)). W tym stanie przekrój traci swoją sztywność na zginanie i zaczyna zachowywać się jak przegub, zdolny do przenoszenia stałego momentu \(M_{pl}\). Nazywamy go przegubem plastycznym.

Kluczowe parametry przekroju i nośność graniczna

Zdolność przekroju do przenoszenia momentów w poszczególnych stanach opisują dwa wskaźniki:

• Sprężysty wskaźnik wytrzymałości na zginanie (\(W_{el}\)): Określa nośność w stanie sprężystym. Jest to stosunek momentu bezwładności przekroju (\(I_y\)) do odległości najdalszego włókna od osi obojętnej (\(z_{max}\)):
  \( W_{el} = \frac{I_y}{z_{max}} \), co prowadzi do \( M_{el} = W_{el} \cdot R_e \).
• Plastyczny wskaźnik wytrzymałości na zginanie (\(W_{pl}\)): Określa nośność w stanie pełnego uplastycznienia. Jest to suma momentów statycznych obu połówek pola przekroju względem osi plastycznej:
  \( W_{pl} = S_{pl,1} + S_{pl,2} \), co prowadzi do \( M_{pl} = W_{pl} \cdot R_e \).

Nośność graniczna konstrukcji – Utworzenie mechanizmu

Pojawienie się jednego przegubu plastycznego nie zawsze oznacza zniszczenia całej konstrukcji.

• W konstrukcjach statycznie wyznaczalnych, powstanie już pierwszego przegubu plastycznego jest równoznaczne z utratą stabilności. Układ staje się mechanizmem (układem geometrycznie zmiennym). W tym przypadku graniczne obciążenie plastyczne (powodujące \(M_{pl}\)) jest równe nośności granicznej.
• W konstrukcjach statycznie niewyznaczalnych, powstanie pierwszego przegubu plastycznego jedynie obniża stopień statycznej niewyznaczalności. Konstrukcja nadal może przenosić rosnące obciążenie. Zniszczenie następuje dopiero wtedy, gdy utworzy się wystarczająca liczba przegubów plastycznych (\(n+1\), gdzie \(n\) to stopień statycznej niewyznaczalności), aby zamienić konstrukcję w mechanizm. Obciążenie, które to powoduje, nazywamy obciążeniem granicznym (nośnością graniczną).

Metody wyznaczania nośności granicznej belek

Istnieją dwie główne metody oparte na twierdzeniach ekstremalnych teorii plastyczności, które pozwalają bezpośrednio obliczyć nośność graniczną, pomijając analizę stanów pośrednich.

Podejście statyczne (Metoda pól statycznie dopuszczalnych)

Ta metoda bazuje na twierdzeniu o oszacowaniu dolnym. Jej idea polega na znalezieniu takiego rozkładu momentów zginających \(M(x)\), który spełnia jednocześnie dwa warunki:

1. Warunek równowagi: Wykres momentów musi być w równowadze z obciążeniem granicznym \(P^*\).
2. Warunek plastyczności: W żadnym punkcie konstrukcji wartość momentu nie może przekroczyć granicznego momentu plastycznego (\(|M(x)| \le M_{pl}\)).

Każde obciążenie \(P^*\) znalezione w ten sposób jest dolnym oszacowaniem rzeczywistej nośności granicznej. Zgodnie z twierdzeniem, największe spośród statycznie dopuszczalnych obciążeń granicznych jest rzeczywistą nośnością graniczną. Metoda ta jest uważana za "bezpieczną", ponieważ każda znaleziona wartość nie zawyża rzeczywistej nośności.

Podejście kinematyczne (Metoda pól kinematycznie dopuszczalnych)

Ta metoda opiera się na twierdzeniu o oszacowaniu górnym i wykorzystuje zasadę prac wirtualnych. Procedura wygląda następująco:

1. Założenie mechanizmu zniszczenia: Zakładamy a priori, w których miejscach powstaną przeguby plastyczne, aby zamienić konstrukcję w mechanizm (np. w miejscach ekstremów momentów sprężystych).
2. Analiza prac wirtualnych: Nadajemy temu mechanizmowi nieskończenie mały wirtualny obrót \(\theta\) w jednym z przegubów.
3. Obliczenie pracy sił zewnętrznych (\(L_z\)): Obliczamy pracę, jaką wykonałoby obciążenie graniczne \(P^*\) na wirtualnych przemieszczeniach (\(\Delta\)) wynikających z obrotu \(\theta\). Na przykład: \(L_z = P^* \cdot \Delta\).
4. Obliczenie pracy sił wewnętrznych (\(L_w\)): Obliczamy pracę rozproszoną w przegubach plastycznych. Jest to suma iloczynów granicznych momentów plastycznych \(M_{pl}\) i kątów obrotu w przegubach. Na przykład: \(L_w = \sum M_{pl} \cdot \theta_i\).
5. Porównanie prac: Z zasady prac wirtualnych \(L_z = L_w\), z czego wyznaczamy wartość obciążenia granicznego \(P^*\).

Ponieważ lokalizacja przegubów jest zakładana, musimy rozważyć wszystkie możliwe, kinematycznie dopuszczalne schematy zniszczenia. Zgodnie z twierdzeniem, najmniejsze spośród tak obliczonych obciążeń granicznych jest rzeczywistą nośnością graniczną. Ta metoda daje "górne oszacowanie" – wynik może być równy lub większy od rzeczywistej nośności.

Metoda "wprost" – analiza krok po kroku

Podejście to polega na stopniowym zwiększaniu obciążenia i śledzeniu kolejnych faz pracy konstrukcji: od stanu w pełni sprężystego, przez pojawienie się pierwszego przegubu plastycznego, aż do utworzenia mechanizmu. Jest to metoda bardzo pracochłonna, ale doskonale ilustruje fizyczne zjawisko redystrybucji momentów, które zachodzi w konstrukcjach statycznie niewyznaczalnych.

Cały proces przebiega w kilku kluczowych etapach:

Etap 1: Analiza sprężysta i lokalizacja pierwszego przegubu

Na samym początku musimy potraktować belkę jako w pełni sprężystą. Rozwiązujemy ją jedną z metod dla układów hiperstatycznych (np. metodą sił, metoda Clebscha (tak, da się tą metodą rozwiązywać układy statycznie niewyznaczalne), metoda Menabrei-Castigliano), aby uzyskać wykres momentów zginających \(M_{el}(x)\) w układzie statycznie niewyznaczalnym. Z tego wykresu odczytujemy miejsce, w którym występuje absolutnie największy moment co do wartości, oznaczmy go jako \(|M_{max, el}|\). To właśnie w tym przekroju (np. w utwierdzeniu lub pod jedną z sił) jako pierwszy utworzy się przegub plastyczny.

Etap 2: Utworzenie nowego, statycznie wyznaczalnego układu

Gdy obciążenie wzrośnie na tyle, że \(|M_{max, el}|\) osiągnie wartość \(M_{pl}\), w tym miejscu powstaje przegub plastyczny. Co to oznacza dla naszej jednokrotnie statycznie niewyznaczalnej belki?

• Konstrukcja traci jeden więz wewnętrzny (sztywność na zginanie w tym punkcie).
• Jednokrotnie statycznie niewyznaczalny układ staje się układem statycznie wyznaczalnym.
• W miejscu nowo powstałego przegubu działa teraz stały moment, równy granicznemu momentowi plastycznemu \(M_{pl}\).

Etap 3: Analiza nowego układu i poszukiwanie drugiego przegubu

Teraz analizujemy tę nową, statycznie wyznaczalną belkę. Jest ona obciążona dwiema grupami sił:

1. Oryginalnymi siłami zewnętrznymi (w poniższym przykładzie obliczeniowym są to siły \(2P\) i \(3P\)).
2. Znanym momentem \(M_{pl}\), przyłożonym w miejscu pierwszego przegubu plastycznego.

Naszym celem jest znalezienie, gdzie w tym nowym układzie wystąpi kolejny co do wielkości moment zginający, który – przy dalszym wzroście obciążenia \(P\) – jako drugi osiągnie wartość \(M_{pl}\). Aby znaleźć wartość tego momentu, możemy skorzystać z zasady superpozycji:

• Rysujemy wykres momentów \(M_P(x)\) na belce statycznie wyznaczalnej, obciążonej tylko siłami \(2P\) i \(3P\).
• Rysujemy wykres momentów \(M_{Mpl}(x)\) na tej samej belce, obciążonej tylko momentem \(M_{pl}\).
• Sumujemy oba wykresy: \(M(x) = M_P(x) + M_{Mpl}(x)\).

Etap 4: Wyznaczenie nośności granicznej

Konstrukcja ulegnie zniszczeniu (stanie się mechanizmem), gdy drugi przegub plastyczny utworzy się w miejscu nowego maksimum momentu z wykresu \(M(x)\). Wyznaczamy więc nośność graniczną, przyrównując wartość tego nowego maksimum do granicznego momentu plastycznego:

\[ |M_{max}| = M_{pl} \]

Ponieważ wykres \(M(x)\) jest funkcją siły \(P\), powyższe równanie pozwala nam wyliczyć ostateczną, maksymalną wartość siły \(P\), jaką konstrukcja może przenieść. Jest to właśnie poszukiwana nośność graniczna (\(P_{gr}\)).

Przykład obliczeniowy – analiza belki statycznie niewyznaczalnej

Metodę "wprost" oraz dwie metody wyznaczania nośności granicznej (statyczną i kinematyczną) przeanalizujemy na przykładzie jednokrotnie statycznie niewyznaczalnej belki o przekroju prostokątnym \(b \times h = 0.10 \times 0.20\) m. Belka jest obciążona jak na poniższym schemacie i wykonana z materiału, którego granica plastyczności wynosi \(R_e = 245\) MPa.

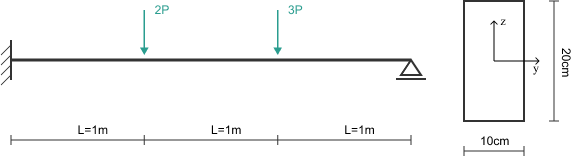
Metoda obliczenia "wprost" rzeczywistej nośności granicznej

Najpierw opiszemy rozwiązanie przykładu "wprost"

Krok 1: Obliczenie granicznych momentów sprężystego i plastycznego

W pierwszej kolejności musimy wyznaczyć charakterystyczne momenty dla zadanego przekroju, które określą jego nośność w zakresie sprężystym i plastycznym.

Wskaźniki wytrzymałości

Ponieważ przekrój jest bisymetryczny, jego oś obojętna zarówno w stanie sprężystym, jak i plastycznym, przechodzi przez jego środek geometryczny.

• Sprężysty wskaźnik wytrzymałości na zginanie: \[ W_{el} = \frac{bh^2}{6} = \frac{0.10 \cdot (0.20)^2}{6} \approx 6.67 \cdot 10^{-4} \, \text{m}^3 \]
• Plastyczny wskaźnik wytrzymałości na zginanie: \[ W_{pl} = \frac{bh^2}{4} = \frac{0.10 \cdot (0.20)^2}{4} = 1.00 \cdot 10^{-3} \, \text{m}^3 \]

Graniczne momenty

Mając wskaźniki, możemy obliczyć graniczne momenty:

• Graniczny moment sprężysty (\(M_{el}\)): \[ M_{el} = R_e \cdot W_{el} = 245 \cdot 10^6 \, \frac{\text{N}}{\text{m}^2} \cdot 6.67 \cdot 10^{-4} \, \text{m}^3 \approx 163.4 \, \text{kNm} \]
• Graniczny moment plastyczny (\(M_{pl}\)): \[ M_{pl} = R_e \cdot W_{pl} = 245 \cdot 10^6 \, \frac{\text{N}}{\text{m}^2} \cdot 1.00 \cdot 10^{-3} \, \text{m}^3 = 245.0 \, \text{kNm} \]

Wartość \(M_{pl}\) jest kluczowa dla dalszej analizy, ponieważ określa maksymalny moment, jaki może przenieść przegub plastyczny.

Krok 2: Analiza momentów w stanie sprężystym

Pierwszym krokiem do znalezienia nośności granicznej jest wyznaczenie wykresu momentów w analizowanej belce w zakresie sprężystym. Ponieważ belka jest jednokrotnie statycznie niewyznaczalna, do znalezienia reakcji (a co za tym idzie, sił wewnętrznych) nie wystarczą same równania równowagi.

Aby rozwiązać ten układ, należy skorzystać z jednej z metod rozwiązywania układów hiperstatycznych, na przykład:

• Metody Maxwella-Mohra (metoda sił) - zobacz Metody energetyczne - Układy statycznie niewyznaczalne
• Metody Menabrea-Castigliano - jak wyżej.
• Metody trzech momentów - jak wyżej.
• Metody Clebscha - zobacz Ugięcia / Układy statycznie niewyznaczalne.

Po rozwiązaniu belki jedną z tych metod uzyskalibyśmy ostateczny wykres momentów zginających w stanie sprężystym (patrz rysunek 2). Analiza tego wykresu jest kluczowa, ponieważ wskazuje miejsce, w którym powstaje moment o wartości ekstremalnej. To właśnie w tym miejscu powstanie pierwszy przegub plastyczny.

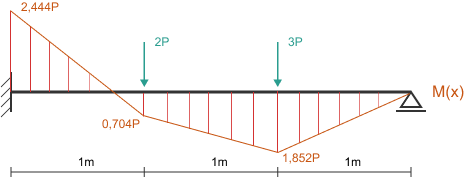
Z przedstawionego wykresu momentów w stanie sprężystym (Rys. 2) wynika jednoznacznie, że moment o największej wartości bezwzględnej występuje w utwierdzeniu. Jego wartość wynosi:

\[ |M_{max, el}| = 2.444 P \]

To właśnie w tym miejscu, przy dalszym wzroście obciążenia, materiał zacznie się uplastyczniać. Możemy teraz obliczyć dwie charakterystyczne wartości obciążenia.

Graniczne obciążenie sprężyste (\(P_{el}\))

Jest to taka wartość siły \(P\), przy której moment w utwierdzeniu osiąga graniczną wartość sprężystą \(M_{el}\). Przyrównując te wartości, obliczamy:

\[ 2.444 P_{el} = M_{el} = 163.4 \, \text{kNm} \] \[ P_{el} = \frac{163.4 \, \text{kNm}}{2.444} \approx 66.86 \, \text{kN} \]

Po przekroczeniu tej wartości obciążenia, w skrajnych włóknach przekroju w utwierdzeniu pojawiają się pierwsze odkształcenia plastyczne.

Graniczne obciążenie plastyczne (\(P_{pl}\))

Zwiększanie obciążenia ponad \(P_{el}\) prowadzi do rozwoju stref plastycznych. Graniczne obciążenie plastyczne to taka wartość siły \(P\), przy której w miejscu maksymalnego momentu (w utwierdzeniu) powstaje pierwszy przegub plastyczny. Obliczamy je z zależności:

\[ 2.444 P_{pl} = M_{pl} = 245.0 \, \text{kNm} \] \[ P_{pl} = \frac{245.0 \, \text{kNm}}{2.444} \approx 100.25 \, \text{kN} \]

Wartość \(P_{pl} \approx 100.25 \, \text{kN}\) nie jest jeszcze nośnością graniczną całej konstrukcji. W tym momencie belka traci jedynie jeden stopień statycznej niewyznaczalności i staje się układem statycznie wyznaczalnym (belką swobodnie podpartą z przyłożonym momentem \(M_{pl}\) w miejscu dawnego utwierdzenia), zdolnym do dalszego przenoszenia rosnącego obciążenia. Proces zniszczenia nastąpi dopiero wtedy, gdy w tym nowym układzie powstanie kolejny przegub plastyczny.

Etap 4: Analiza układu po powstaniu pierwszego przegubu

W momencie, gdy obciążenie osiągnęło wartość \(P_{pl} \approx 100.25 \, \text{kN}\), w utwierdzeniu (punkt A) utworzył się pierwszy przegub plastyczny. Skoro moment w stanie sprężystym był tam ujemny (rozciągał górne włókna), to przegub ten będzie przenosił stały moment \(M_{pl}\) działający w tym samym kierunku.

Nasza konstrukcja staje się teraz belką swobodnie podpartą, obciążoną siłami zewnętrznymi \(2P\) i \(3P\) oraz stałym momentem \(M = M_{pl} = 245.0 \, \text{kNm}\), przyłożonym na lewym końcu.

Dalsze zwiększanie siły \(P\) będzie powodować wzrost momentów w przęśle, aż do momentu, w którym w kolejnym punkcie moment osiągnie wartość \(M_{pl}\), tworząc drugi przegub i zamieniając belkę w mechanizm. Naszym celem jest znalezienie tej granicznej wartości \(P_{gr}\).

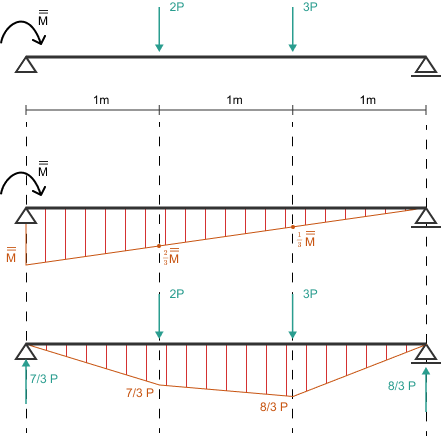
Zgodnie z zasadą superpozycji, uwzględniając właściwy znak momentu plastycznego, momenty w kluczowych punktach B i C wynoszą:

\[ M_B = \frac{7}{3}P - \frac{2}{3}M_{pl} \] \[ M_C = \frac{8}{3}P - \frac{1}{3}M_{pl} \]

Etap 5: Lokalizacja drugiego przegubu i wyznaczenie nośności granicznej

Teraz musimy ustalić, który z tych momentów – \(M_B\) czy \(M_C\) – jako pierwszy osiągnie wartość \(|M_{pl}|\) przy dalszym wzroście siły \(P\). Zwróćmy uwagę, że oba momenty w przęśle będą dodatnie (rozciąganie dolnych włókien). Drugi przegub plastyczny powstanie tam, gdzie moment jako pierwszy osiągnie wartość \(+M_{pl}\).

Sprawdźmy, jaka wartość \(P\) jest potrzebna, aby każdy z tych momentów osiągnął \(M_{pl}\):

• Warunek dla punktu B (\(M_B = M_{pl}\)): \[ \frac{7}{3}P_B = M_{pl} + \frac{2}{3}M_{pl} = \frac{5}{3}M_{pl} \implies 7P_B = 5M_{pl} \implies P_B = \frac{5}{7}M_{pl} \approx 0.714 M_{pl} \]
• Warunek dla punktu C (\(M_C = M_{pl}\)): \[ \frac{8}{3}P_C = M_{pl} + \frac{1}{3}M_{pl} = \frac{4}{3}M_{pl} \implies 8P_C = 4M_{pl} \implies P_C = \frac{4}{8}M_{pl} = \frac{1}{2}M_{pl} = 0.5 M_{pl} \]

Porównując obie wartości, widzimy, że potrzeba mniejszego obciążenia, aby moment w punkcie C osiągnął wartość plastyczną (\(0.5 M_{pl} < 0.714 M_{pl}\)). Oznacza to, że drugi przegub plastyczny powstanie w punkcie C.

Nośność graniczna (\(P_{gr}\)) jest więc określona przez warunek dla punktu C:

\[ P_{gr} = \frac{1}{2} M_{pl} \]

Podstawiając obliczoną wcześniej wartość \(M_{pl} = 245.0 \, \text{kNm}\), otrzymujemy ostateczną nośność graniczną belki:

\[ P_{gr} = \frac{1}{2} \cdot 245.0 \, \text{kNm} = 122.5 \, \text{kN} \]

Wniosek: Ostateczna nośność graniczna wynosi \(P_{gr} = 122.5 \, \text{kN}\). Wynik ten jest większy niż graniczne obciążenie plastyczne (\(P_{pl} \approx 100.25 \, \text{kN}\)), co jest logiczne i poprawne. Różnica \(\Delta P = 122.5 - 100.25 = 22.25 \, \text{kN}\) pokazuje, o ile więcej obciążenia konstrukcja była w stanie przenieść dzięki redystrybucji momentów po uplastycznieniu utwierdzenia.

Metoda pól kinematycznie dopuszczalnych (podejście kinematyczne)

Podejście kinematyczne opiera się na twierdzeniu o oszacowaniu górnym i jest często najszybszym sposobem na wyznaczenie nośności granicznej. Metoda ta nie analizuje sił i momentów wewnątrz konstrukcji, a zamiast tego skupia się na energii i pracy w momencie zniszczenia, wykorzystując zasadę prac wirtualnych (ZPW).

Idea metody

W tym podejściu rozważamy konstrukcję w jej stanie granicznym, czyli jako mechanizm. Oznacza to, że zakładamy a priori, gdzie powstaną przeguby plastyczne, które uczynią belkę geometrycznie zmienną. Następnie nadajemy temu mechanizmowi nieskończenie mały, wirtualny obrót i porównujemy pracę wykonaną przez siły zewnętrzne z pracą rozproszoną w przegubach plastycznych.

Zasada prac wirtualnych mówi, że:

Suma prac wirtualnych sił zewnętrznych (\(L_z\)) jest równa sumie prac wirtualnych sił wewnętrznych (\(L_w\)).

W naszym przypadku:

• Siły zewnętrzne to obciążenie graniczne \(P_{gr}\), które chcemy znaleźć.
• Siły wewnętrzne to stałe, graniczne momenty plastyczne \(M_{pl}\) działające w przegubach.

Problem: Gdzie powstaną przeguby?

Największym wyzwaniem tej metody jest konieczność prawidłowego założenia lokalizacji przegubów plastycznych. Dobrą wskazówką są miejsca, gdzie wykres momentów w stanie sprężystym osiągał wartości ekstremalne. Dla naszej belki są to:

• Utwierdzenie (punkt A).
• Przekrój pod siłą 2P (punkt B).
• Przekrój pod siłą 3P (punkt C).

Ponieważ nie mamy pewności, który z tych scenariuszy jest poprawny, musimy rozważyć wszystkie kinematycznie dopuszczalne schematy zniszczenia. Następnie, zgodnie z twierdzeniem o oszacowaniu górnym, rzeczywistą nośnością graniczną będzie najmniejsza z obliczonych wartości.

Schemat pierwszy: Zniszczenie z przegubami w A i C

Zacznijmy od schematu, który wydaje się najbardziej prawdopodobny na podstawie analizy historycznej – z przegubami w utwierdzeniu (A) i pod siłą 3P (C).

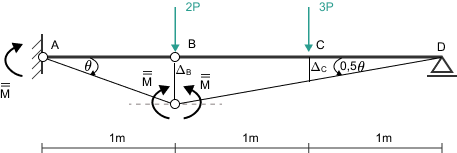
1. Analiza geometryczna planu przemieszczeń

Nadajemy mechanizmowi wirtualny obrót \(\theta\) w przegubie plastycznym w punkcie A. Cała belka, jako ciało sztywne między przegubami A i C, obraca się wokół punktu A. Jednocześnie, aby mechanizm był możliwy, przegub w C musi się ugiąć, a odcinek CD obraca się wokół podpory D. Dla uproszczenia przyjmijmy wirtualny obrót \(\theta\) w przegubie A.

• Kąt obrotu w przegubie A: \(\theta_A = \theta\).
• Przemieszczenie pionowe w punkcie B: \(\Delta_B = \theta \cdot L_{AB} = \theta \cdot 1 \, \text{m}\).
• Przemieszczenie pionowe w punkcie C: \(\Delta_C = \theta \cdot L_{AC} = \theta \cdot 2 \, \text{m}\).
• Całkowity kąt obrotu w przegubie C: Odcinek AC obraca się o \(\theta\). Odcinek CD obraca się o kąt \(\theta_D = \Delta_C / L_{CD} = (2\theta) / 1 = 2\theta\). Całkowity kąt załamania w przegubie C wynosi \(\theta_C = \theta + \theta_D = \theta + 2\theta = 3\theta\).

2. Praca sił zewnętrznych (\(L_z\))

Pracę wykonują siły \(2P\) i \(3P\) na swoich wirtualnych przemieszczeniach:

\[ L_z = (2P_{gr} \cdot \Delta_B) + (3P_{gr} \cdot \Delta_C) = (2P_{gr} \cdot \theta) + (3P_{gr} \cdot 2\theta) = 2P_{gr}\theta + 6P_{gr}\theta = 8P_{gr}\theta \]

3. Praca sił wewnętrznych (\(L_w\))

Praca jest rozpraszana przez momenty plastyczne \(M_{pl}\) w przegubach plastycznych. Zgodnie z naszym schematem, przeguby mamy w A i C. Pracę wykonują momenty \(M_{pl}\) na kątach obrotu w tych przegubach.

\[ L_w = (M_{pl} \cdot |\theta_A|) + (M_{pl} \cdot |\theta_C|) = (M_{pl} \cdot \theta) + (M_{pl} \cdot 3\theta) = 4M_{pl}\theta \]

4. Porównanie prac i wyznaczenie \(P_{gr}\)

Przyrównujemy pracę zewnętrzną i wewnętrzną: \(L_z = L_w\)

\[ 8P_{gr}\theta = 4M_{pl}\theta \] \[ P_{gr,1} = \frac{4}{8}M_{pl} = \frac{1}{2}M_{pl} \]

Podstawiając wartość \(M_{pl} = 245.0 \, \text{kNm}\):

\[ P_{gr,1} = \frac{1}{2} \cdot 245.0 \, \text{kNm} = 122.5 \, \text{kN} \]

Wartość \(P_{gr,1}\) jest pierwszą, możliwą nośnością graniczną, odpowiadającą założonemu schematowi zniszczenia.

Schemat drugi: Zniszczenie z przegubami w A i B

Teraz rozważmy drugi prawdopodobny scenariusz, w którym przeguby plastyczne tworzą się w utwierdzeniu (A) i pod siłą 2P (punkt B).

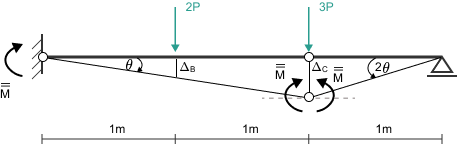
1. Analiza geometryczna planu przemieszczeń

W tym przypadku mechanizm tworzy się inaczej. Zakładamy wirtualny obrót \(\theta\) w przegubie plastycznym w punkcie A. Odcinek AB, jako ciało sztywne, obraca się wokół punktu A. Odcinek BD (od siły 2P do podpory D) obraca się wokół podpory D.

• Kąt obrotu w przegubie A: \(\theta_A = \theta\).
• Przemieszczenie pionowe w punkcie B: \(\Delta_B = \theta \cdot L_{AB} = \theta \cdot 1 \, \text{m}\).
• Kąt obrotu odcinka BD wokół podpory D: \(\theta_D = \Delta_B / L_{BD} = \theta / 2 \, \text{m} = 0.5\theta\).
• Całkowity kąt załamania w przegubie B: \(\theta_B = \theta + \theta_D = \theta + 0.5\theta = 1.5\theta\).
• Przemieszczenie pionowe w punkcie C: Punkt C leży na obracającym się odcinku BD. Jego przemieszczenie wynosi: \(\Delta_C = \theta_D \cdot L_{CD} = (0.5\theta) \cdot 1 \, \text{m} = 0.5\theta\).

2. Praca sił zewnętrznych (\(L_z\))

Pracę wykonują siły \(2P\) i \(3P\) na swoich wirtualnych przemieszczeniach:

\[ L_z = (2P_{gr} \cdot \Delta_B) + (3P_{gr} \cdot \Delta_C) = (2P_{gr} \cdot \theta) + (3P_{gr} \cdot 0.5\theta) = 2P_{gr}\theta + 1.5P_{gr}\theta = 3.5P_{gr}\theta \]

3. Praca sił wewnętrznych (\(L_w\))

Praca jest rozpraszana przez momenty plastyczne \(M_{pl}\) w założonych przegubach plastycznych, czyli w punktach A i B.

\[ L_w = (M_{pl} \cdot |\theta_A|) + (M_{pl} \cdot |\theta_B|) = (M_{pl} \cdot \theta) + (M_{pl} \cdot 1.5\theta) = 2.5M_{pl}\theta \]

4. Porównanie prac i wyznaczenie \(P_{gr}\)

Przyrównujemy pracę zewnętrzną i wewnętrzną: \(L_z = L_w\)

\[ 3.5P_{gr}\theta = 2.5M_{pl}\theta \] \[ P_{gr,2} = \frac{2.5}{3.5}M_{pl} = \frac{5}{7}M_{pl} \]

Podstawiając wartość \(M_{pl} = 245.0 \, \text{kNm}\):

\[ P_{gr,2} = \frac{5}{7} \cdot 245.0 \, \text{kNm} = 175.0 \, \text{kN} \]

Wnioski z analizy kinematycznej

Porównując nośności graniczne obliczone dla obu schematów:

• Schemat 1 (przeguby w A i C): \(P_{gr,1} = 122.5 \, \text{kN}\)
• Schemat 2 (przeguby w A i B): \(P_{gr,2} = 175.0 \, \text{kN}\)

Zgodnie z twierdzeniem o oszacowaniu górnym, rzeczywistą nośnością graniczną jest najmniejsza z obliczonych wartości. Zatem:

\[ P_{gr} = \min(P_{gr,1}, P_{gr,2}) = 122.5 \, \text{kN} \]

Wniosek jest taki, że belka ulegnie zniszczeniu według pierwszego schematu, z przegubami plastycznymi w utwierdzeniu (A) i pod siłą 3P (C), a jej rzeczywista nośność graniczna nie będzie większa niż \(P_{gr} = 122.5 \, \text{kN}\).

Metoda pól statycznie dopuszczalnych (podejście statyczne)

Podejście statyczne bazuje na twierdzeniu o oszacowaniu dolnym. Jego celem jest znalezienie takiego rozkładu momentów zginających w konstrukcji, który jest w równowadze z obciążeniem granicznym i jednocześnie nigdzie nie przekracza granicznego momentu plastycznego. Zgodnie z twierdzeniem, rzeczywistą nośnością graniczną będzie największa ze wszystkich statycznie dopuszczalnych wartości.

Schemat pierwszy: Przeguby plastyczne w A i B

Zakładamy, że przeguby powstaną w utwierdzeniu (A) i pod siłą 2P (punkt B). Zgodnie z analizą sprężystą, przyjmujemy znaki momentów:

\[ M_A = -M_{pl} \] \[ M_B = +M_{pl} \]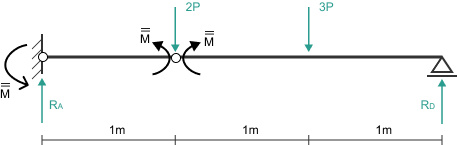

1. Analiza równowagi

Zapisujemy trzy równania równowagi, rozpatrując momenty po lewej i prawej stronie przegubu B.

• Suma momentów dla lewej części (odcinka AB) względem przegubu B: \[ \sum M_B^{lewa} = 0 \implies M_A + (R_A \cdot L_{AB}) - M_B = 0 \] \[ -M_{pl} + (R_A \cdot 1) - M_{pl} = 0 \implies R_A = 2M_{pl} \]
• Suma momentów dla prawej części (odcinka BD) względem przegubu B: \[ \sum M_B^{prawa} = 0 \implies M_{pl} + (3P \cdot 1) - (R_D \cdot 2) = 0 \] \[ 2R_D = M_{pl} + 3P \]
• Suma rzutów sił na oś Y dla całej belki: \[ \sum F_y = 0 \implies R_A - 2P - 3P + R_D = 0 \implies R_A + R_D = 5P \]

Mamy układ trzech równań. Z pierwszego równania wiemy, że \(R_A = 2M_{pl}\). Podstawiamy to do trzeciego równania:

\[ 2M_{pl} + R_D = 5P \implies R_D = 5P - 2M_{pl} \]

Teraz podstawiamy wyznaczone \(R_D\) do (poprawionego) drugiego równania:

\[ 2(5P - 2M_{pl}) = M_{pl} + 3P \] \[ 10P - 4M_{pl} = M_{pl} + 3P \] \[ 7P = 5M_{pl} \implies P = \frac{5}{7}M_{pl} \]

2. Weryfikacja warunku plastyczności

Obliczmy moment w punkcie C przy obciążeniu \(P = 5M_{pl}/7\) (w punkcie A i B wiemy że moment jest równy \(M_{pl} \) ). Reakcja \(R_D\) wynosi: \[ R_D = 5P - 2M_{pl} = 5(\frac{5}{7}M_{pl}) - 2M_{pl} = \frac{25}{7}M_{pl} - \frac{14}{7}M_{pl} = \frac{11}{7}M_{pl} \] Moment w punkcie C, liczony od prawej strony, wynosi: \[ M_C = R_D \cdot L_{CD} = (\frac{11}{7}M_{pl}) \cdot 1 \approx 1.57 M_{pl} \]

Wniosek: Otrzymaliśmy \(|M_C| > M_{pl}\). Warunek plastyczności został złamany. Oznacza to, że założone pole momentów nie jest statycznie dopuszczalne, a ten schemat zniszczenia jest niemożliwy.

Schemat drugi: Przeguby plastyczne w A i C

Zakładamy przeguby w utwierdzeniu (A) i pod siłą 3P (punkt C). Przyjmujemy znaki momentów:

\[ M_A = -M_{pl} \] \[ M_C = +M_{pl} \]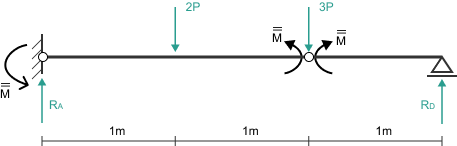

1. Analiza równowagi

• Suma momentów dla lewej części (odcinka AC) względem przegubu C: \[ \sum M_C^{lewa} = 0 \implies -M_{pl} + (R_A \cdot 2) - (2P \cdot 1) - M_{pl} = 0 \implies 2R_A - 2P = 2M_{pl} \implies R_A - P = M_{pl} \]
• Suma momentów dla prawej części (odcinka CD) względem przegubu C: \[ \sum M_C^{prawa} = 0 \implies M_{pl} - (R_D \cdot 1) = 0 \implies R_D = M_{pl} \]
• Suma rzutów sił na oś Y dla całej belki: \[ \sum F_y = 0 \implies R_A - 2P - 3P + R_D = 0 \implies R_A + R_D = 5P \]

Z drugiego równania mamy \(R_D = M_{pl}\). Podstawiamy to do trzeciego równania:

\[ R_A + M_{pl} = 5P \implies R_A = 5P - M_{pl} \]

Teraz podstawiamy wyznaczone \(R_A\) do pierwszego równania:

\[ (5P - M_{pl}) - P = M_{pl} \] \[ 4P = 2M_{pl} \implies P = \frac{2}{4}M_{pl} = \frac{1}{2}M_{pl} \]

2. Weryfikacja warunku plastyczności

Sprawdźmy moment w punkcie B przy obciążeniu \(P = M_{pl}/2\) (w punkcie A i C wiemy że moment jest równy \(M_{pl} \) ). Najpierw obliczmy reakcję \(R_A\):

\[ R_A = 5P - M_{pl} = 5(\frac{M_{pl}}{2}) - M_{pl} = 2.5 M_{pl} - M_{pl} = 1.5 M_{pl} \]

Teraz moment w punkcie B:

\[ M_B = M_A + R_A \cdot L_{AB} = -M_{pl} + (1.5 M_{pl} \cdot 1) = +0.5 M_{pl} \]

Wniosek: Sprawdzamy wszystkie wartości momentów w kluczowych punktach:

• \(|M_A| = M_{pl}\) (OK)
• \(|M_B| = 0.5 M_{pl} < M_{pl}\) (OK)
• \(|M_C| = M_{pl}\) (OK)

Wszystkie warunki (równowagi i plastyczności) są spełnione. Oznacza to, że ten schemat jest statycznie dopuszczalny. Nośność graniczna dla tego przypadku wynosi \(P_2 = M_{pl}/2\).

Wnioski końcowe z analizy statycznej

Porównując nośności graniczne obliczone dla obu schematów (z których tylko drugi okazał się w pełni poprawny po weryfikacji), wybieramy większą wartość spośród tych, które są statycznie dopuszczalne. W tym przypadku mamy tylko jedno takie rozwiązanie, co silnie sugeruje, że jest ono tym właściwym.

\[ P_{gr} = \frac{1}{2}M_{pl} \]

Podstawiając wartość \(M_{pl}\), otrzymujemy:

\[ P_{gr} = \frac{245.0 \, \text{kNm}}{2} = 122.5 \, \text{kN} \]

Wynik ten jest identyczny z wynikiem uzyskanym z metody kinematycznej, co potwierdza, że jest to rzeczywista nośność graniczna konstrukcji.