Środek i wskaźnik plastyczny

Wprowadzenie – Kluczowe parametry w analizie plastycznej

Aby obliczyć graniczny moment plastyczny (\(M_{pl}\)), który jest fundamentem teorii nośności granicznej, musimy najpierw wyznaczyć dwa kluczowe parametry geometryczne przekroju: jego oś plastyczną oraz plastyczny wskaźnik wytrzymałości na zginanie (\(W_{pl}\)). W przeciwieństwie do analizy sprężystej, gdzie kluczową rolę odgrywał środek ciężkości i moment bezwładności, w analizie plastycznej operujemy na pojęciach związanych z równowagą pól powierzchni przekroju.

Oś plastyczna

Oś plastyczna to oś prostopadła do płaszczyzny zginania, która w stanie pełnego uplastycznienia staje się osią obojętną. Jej najważniejszą właściwością jest to, że dzieli ona całkowite pole przekroju poprzecznego (\(A\)) na dwie równe części:

\[ A_1 = A_2 = \frac{A}{2} \]

gdzie \(A_1\) to pole części rozciąganej, a \(A_2\) to pole części ściskanej. Dla przekrojów symetrycznych (jak prostokąt czy dwuteownik o równych półkach) oś plastyczna pokrywa się z osią symetrii. Jednak dla przekrojów niesymetrycznych jej położenie trzeba obliczyć.

Plastyczny wskaźnik wytrzymałości na zginanie (\(W_{pl}\))

Plastyczny wskaźnik wytrzymałości (\(W_{pl}\)) jest miarą zdolności przekroju do przenoszenia momentu w stanie pełnego uplastycznienia. Definiuje się go jako sumę momentów statycznych obu połówek pola przekroju względem osi plastycznej.

\[ W_{pl} = S_{pl,1} + S_{pl,2} \]

gdzie \(S_{pl,1}\) i \(S_{pl,2}\) to momenty statyczne pola rozciąganego (\(A_1\)) i ściskanego (\(A_2\)) względem osi plastycznej.

Przykład: Obliczenia dla niesymetrycznego dwuteownika

Przeanalizujmy dwuteownik o różnych szerokościach półek, jak na rysunku poniżej. Wszystkie wymiary podano w centymetrach.

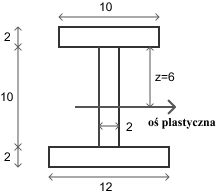
Krok 1: Obliczenie pola i lokalizacja osi plastycznej

Najpierw obliczamy całkowite pole przekroju:

\[ A = A_{pasa, góra} + A_{środnika} + A_{pasa, dół} = (10 \cdot 2) + (2 \cdot 10) + (12 \cdot 2) = 20 + 20 + 24 = 64 \, \text{cm}^2 \]

Oś plastyczna musi podzielić to pole na dwie równe części o powierzchni \(A/2 = 32 \, \text{cm}^2\). Aby znaleźć jej położenie, zaczynamy sumować pola od góry:

• Pole górnego pasa: \(A_{pasa, góra} = 20 \, \text{cm}^2\).

Ponieważ \(20 < 32\), wiemy, że oś plastyczna musi przebiegać gdzieś wewnątrz środnika. Potrzebujemy "dobrać" z niego brakujące \(32 - 20 = 12 \, \text{cm}^2\). Niech \(z\) będzie odległością od spodu górnego pasa w głąb środnika, do której sięga górna połówka pola.

\[ A_{środnika, góra} = 2 \cdot z = 12 \, \text{cm}^2 \implies z = 6 \, \text{cm} \]

Oznacza to, że oś plastyczna leży 6 cm poniżej styku górnego pasa ze środnikiem (lub 8 cm od górnej krawędzi przekroju).

Krok 2: Obliczenie plastycznego wskaźnika wytrzymałości \(W_{pl}\)

Teraz obliczamy momenty statyczne obu połówek pola względem znalezionej osi plastycznej.

• Moment statyczny górnej połówki (\(S_{pl,1}\)):

  Składa się z momentu statycznego górnego pasa i górnej części środnika.

  • Odległość środka ciężkości pasa od osi plastycznej: \(6 + 1 = 7 \, \text{cm}\).
  • Odległość środka ciężkości górnej części środnika od osi plastycznej: \(6 / 2 = 3 \, \text{cm}\).
  \[ S_{pl,1} = (20 \, \text{cm}^2 \cdot 7 \, \text{cm}) + (12 \, \text{cm}^2 \cdot 3 \, \text{cm}) = 140 + 36 = 176 \, \text{cm}^3 \]
• Moment statyczny dolnej połówki (\(S_{pl,2}\)):

  Składa się z momentu statycznego dolnej części środnika (o wysokości \(10-6=4\) cm) i dolnego pasa.

  • Odległość środka ciężkości dolnej części środnika od osi plastycznej: \(4 / 2 = 2 \, \text{cm}\).
  • Odległość środka ciężkości dolnego pasa od osi plastycznej: \(4 + 1 = 5 \, \text{cm}\).
  \[ S_{pl,2} = ( (2 \cdot 4) \, \text{cm}^2 \cdot 2 \, \text{cm}) + (24 \, \text{cm}^2 \cdot 5 \, \text{cm}) = 16 + 120 = 136 \, \text{cm}^3 \]

Ostatecznie, plastyczny wskaźnik wytrzymałości to suma obu momentów statycznych:

\[ W_{pl} = S_{pl,1} + S_{pl,2} = 176 + 136 = 312 \, \text{cm}^3 \]

Znając \(W_{pl}\), możemy łatwo obliczyć graniczny moment plastyczny dla tego przekroju: \(M_{pl} = W_{pl} \cdot R_e\).