Zginanie proste

Wprowadzenie do zginania

Zginanie jest jednym z kluczowych zagadnień w wytrzymałości materiałów, odgrywającym istotną rolę w projektowaniu i analizie elementów konstrukcyjnych. Zginanie dzielimy na dosyć szerokie i różnorodne poddziały jak zginanie proste, zginanie poprzeczne i zginanie ukośne. W trzech osobnych wstępach opiszemy krótko każde z tych zagadnień.

Zginanie proste to rodzaj zginania, który występuje, gdy obciążenie działa w jednej płaszczyźnie i powoduje wygięcie elementu w tej samej płaszczyźnie. Jest to najprostszy typ zginania w praktyce inżynierskiej.

Analiza zginania prostego

Podczas analizy zginania prostego obliczamy momenty zginające oraz naprężenia w przekroju poprzecznym elementu, aby zapewnić, że materiał i konstrukcja wytrzymają planowane obciążenia bez uszkodzeń.

Naprężenia normalne w zginaniu prostym

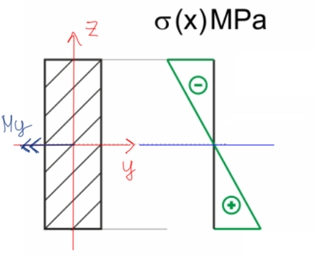
Równanie naprężenia normalnego uwzględniające działanie momentu zginającego w jednej płaszczyźnie (tutaj płaszczyzna obciążenia jest pionowo, wektor momentu powstaje w płaszczyźnie prostopadłej do płaszczyzny zginania, czyli poziomo):

$$\sigma(x) = \frac{M_y}{I_y} \cdot z$$

gdzie:

• \( \sigma \) to naprężenie normalne,
• \( M_y \) to moment zginający,
• \( z \) to odległość od osi obojętnej do punktu przekroju, w którym chcemy obliczyć naprężenia,
• \( I_y \) to moment bezwładności przekroju poprzecznego

Dla bardziej dociekliwych - wzór który opisaliśmy powyżej można wykorzystać dzięki założeniu dla zginania hipotezy płaskich przekrojów Bernoulliego.

Wyprowadzenie tego wzoru znajdziecie tutaj.

Rys. 1. Wykres naprężeń normalnych dla przypadku zginania prostego

Oś obojętna i wektor momentu

Oczywiście kwestią założenia jest nazewnictwo osi przekroju poprzecznego, w przykładzie powyżej to y,z – z tymi oznaczeniami związane są oznaczenia we wzorze na naprężenia. Zwrot wektora momentu zależny jest od wykresu momentu, a konkretnie od tego czy rozciąga włókna dolne czy górne w punkcie belki który analizujemy (najczęściej analizujemy punkt w którym występuje największy moment na całej belce).

W elemencie zginanym prosto występuje oś obojętna, czyli linia w przekroju poprzecznym, która nie jest ani rozciągana, ani ściskana. Pokrywa się ona zawsze z wektorem momentu i dzieli przekrój na część rozciąganą i ściskaną.

Zrozumienie zginania prostego jest podstawą do dalszych, bardziej skomplikowanych analiz zginania i projektowania wytrzymałych konstrukcji.

Do dyspozycji masz kursy wideo oraz szeroką bazę zadań z rozwiązaniami dla każdego rodzaju zginania osobno.