Wytrzymałość materiałów
Zginanie ukośne
- Wprowadzenie do zginania ukośnego
- Definicja i charakterystyka
- Rzutowanie momentu gnącego na osie główne centralne
- Składowe momentu w osiach y i z
- Oś obojętna w zginaniu ukośnym
- Położenie osi obojętnej
- Miejsce geometryczne punktów zerowych naprężeń
- Naprężenia normalne w zginaniu ukośnym
- Równanie naprężenia normalnego
- Parametry wzoru
- Wykres naprężeń normalnych
- Bryła naprężeń
Wprowadzenie do zginania ukośnego
Zginanie ukośne to rodzaj zginania, w którym kierunek wektora momentu gnącego nie pokrywa się z żadną z głównych osi bezwładności przekroju. Oznacza to, że płaszczyzna działania obciążenia nie jest równoległa do żadnej z tych osi. Rzutując wektor momentu gnącego na główne centralne osie układu, otrzymujemy składowe momentu (M) w osiach (y) i (z).
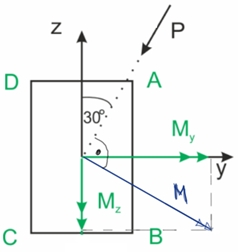
Rys. 1. Zginanie ukośne - rzutowanie momentu na osie główne centralne
Z tego kursu dowiesz się:
- jak wyznaczyć reakcje i narysować wykresy sił wewnętrznych,
- jak narysować rozkład naprężeń normalnych,
- jak wyznaczyć bryłę naprężeń,
- jak wyznaczyć i narysować położenie osi obojętnej,
- jak zwymiarować belkę zginaną ukośnie z warunku wytrzymałości,
- jak wyznaczyć dopuszczalną wartość obciążenia mając dany konkretny przekrój.
Oś obojętna w zginaniu ukośnym
W ogólności oś obojętna nie pokrywa się z linią działania wektora momentu gnącego, choć przechodzi przez środek ciężkości przekroju. Oś obojętna zginania to miejsce geometryczne punktów, dla których naprężenia są równe zero.
Naprężenia normalne w zginaniu ukośnym
Równanie naprężenia normalnego uwzględniające działanie momentu zginającego w kierunku dwóch osi głównych centralnych:
$$\sigma(x) = \frac{-M_y}{I_y} \cdot z - \frac{M_z}{I_z} \cdot y$$
gdzie:
- \( \sigma \) to naprężenie normalne,
- \( M_y, M_z \) to momenty zginające,
- \( y, z \) to odległości od środka ciężkości po osiach głównych centralnych do punktu przekroju w którym chcemy obliczyć naprężenia,
- \( I_y, I_z \) to główne centralne momenty bezwładności przekroju poprzecznego.
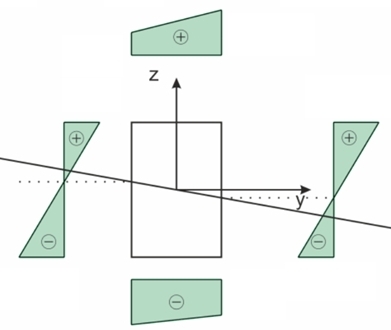
Rys. 2. Przykładowy wykres naprężeń normalnych - zginanie ukośne
Do dyspozycji masz kursy wideo oraz szeroką bazę zadań z rozwiązaniami dla każdego rodzaju zginania osobno.