Przemieszczenia metodą Maxwella-Mohra

Podstawy teoretyczne metody

Metoda Maxwella-Mohra, historycznie wywodząca się z prac Jamesa Clerka Maxwella i rozwinięta do praktycznej postaci przez Christiana Otto Mohra, opiera się na fundamentalnej zasadzie prac wirtualnych. Zasada ta mówi, że praca sił zewnętrznych wykonana na wirtualnych przemieszczeniach jest równa pracy wewnętrznej sił wewnętrznych na odpowiadających im odkształceniach. W kontekście obliczania przemieszczeń, metoda ta wykorzystuje pomysłowy zabieg polegający na analizie dwóch stanów obciążenia:

• Stan rzeczywisty (P): Jest to analizowana konstrukcja poddana działaniu rzeczywistych obciążeń zewnętrznych (sił, momentów, obciążeń ciągłych) lub innych wymuszeń, takich jak zmiana temperatury czy osiadanie podpór. W tym stanie w konstrukcji powstają rzeczywiste siły wewnętrzne (momenty gnące M(x), siły osiowe N(x) i siły tnące T(x)).
• Stan wirtualny (pomocniczy, 1): Jest to ta sama konstrukcja, z której usuwamy wszystkie rzeczywiste obciążenia, a w miejscu i w kierunku, w którym szukamy przemieszczenia, przykładamy wirtualną siłę jednostkową (\(P=1\), jeśli szukamy przemieszczenia liniowego) lub wirtualny moment jednostkowy (\(M=1\), jeśli szukamy kąta obrotu). W tym stanie w konstrukcji powstają wirtualne siły wewnętrzne (\(\bar{M}(x)\), \(\bar{N}(x)\), \(\bar{T}(x)\)).

Jakie przemieszczenia można obliczyć?

Metoda Maxwella-Mohra pozwala obliczyć następujące przemieszczenia:

• Zmiana kąta między jedną i drugą stroną przegubu

Aby obliczyć zmianę kąta między jedną i drugą stroną przegubu należy przyłożyć z dwóch stron przegubu wirtualne momenty jednostkowy M=1 o przeciwnych zwrotach.



• Zmiana odległości między dwoma punktami

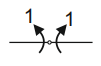
Aby obliczyć zmianę odległości między dwoma punktami ramy należy przyłożyć na prostej łączacej te dwa punkty z dwóch stron wirtualne siły osiowe P=1 o przeciwnych zwrotach.



• Kąt obrotu pręta kratownicy

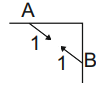
Aby obliczyć kąt obrotu pręta kratownicy należy przyłożyć na pręcie wirtualny moment jednostkowy M=1. Następnie należy ten moment rozłożyć na parę sił dzieląc go przez długość pręta.



• Zmana odległości między dwoma punktami kratownicy

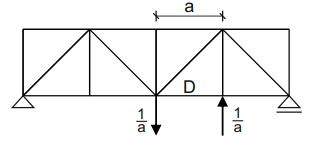
Aby obliczyć zmianę odległości między dwoma punktami kratownicy należy przyłożyć na prostej łączacej te dwa punkty z dwóch stron wirtualne siły osiowe P=1 o przeciwnych zwrotach.



• Zmana kąta między dwoma prętami kratownicy

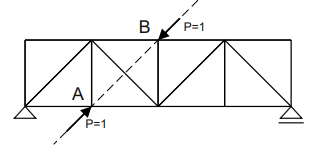
Aby obliczyć zmianę kąta między dwoma prętami kratownicy należy przyłożyć na obu prętach przeciwnie skierowane wirtualne momenty jednostkowy M=1. Następnie należy te momenty rozłożyć na parę sił dzieląc je przez długości prętów.

Wzór całkowy Mohra i jego rozszerzenie

Zestawienie tych dwóch stanów za pomocą zasady prac wirtualnych prowadzi do sformułowania ogólnego wzoru całkowego. Pozwala on obliczyć szukane przemieszczenie (δ) lub kąt obrotu (φ) jako sumę prac wykonanych przez siły wirtualne na odkształceniach rzeczywistych, wynikających z różnych przyczyn.

W najbardziej ogólnej postaci dla ustrojów płaskich, uwzględniając obciążenia mechaniczne, termiczne, osiadanie podpór i podpory sprężyste, wzór ten wygląda następująco:

\[ \delta = \int_L \frac{M(x)\bar{M}(x)}{EI} dx + \int_L \frac{N(x)\bar{N}(x)}{EA} dx + \kappa \int_L \frac{T(x)\bar{T}(x)}{GA} dx + \int_L \alpha_t \Delta T(x) \bar{N}(x) dx + \int_L \frac{\alpha_t \Delta T(x)}{h} \bar{M}(x) dx + \sum_i \frac{R_i \bar{r}_i}{k_i} + \sum_i \delta_i \bar{r}_i \]

Poszczególne składniki tej sumy reprezentują wpływ różnych czynników na całkowite przemieszczenie:

• Wpływ obciążeń mechanicznych (sił i momentów):
  \( \int_L \frac{M(x)\bar{M}(x)}{EI} dx + \int_L \frac{N(x)\bar{N}(x)}{EA} dx +\kappa \int_L \frac{T(x)\bar{T}(x)}{GA} dx \)
  To podstawowa część wzoru, gdzie mnożymy siły wewnętrzne ze stanu rzeczywistego (\(M, N, T\)) przez siły ze stanu wirtualnego (\(\bar{M}, \bar{N}, \bar{T}\)). W praktyce inżynierskiej, dla smukłych belek i ram, często dominuje i wystarcza pierwszy człon, związany ze zginaniem.
• Wpływ równomiernej zmiany temperatury:
  \( \int_L \alpha_t \Delta T(x) \bar{N}(x) dx \)
  Ten człon opisuje przemieszczenie wynikające z wydłużenia lub skrócenia prętów pod wpływem równomiernej zmiany temperatury \(\Delta T(x)\).
  • \(\alpha_t\) – współczynnik rozszerzalności cieplnej materiału.
  • \(\Delta T(x)\) – zmiana temperatury w stanie rzeczywistym.
  • \(\bar{N}(x)\) – wirtualna siła osiowa od obciążenia jednostkowego.
• Wpływ nierównomiernej zmiany temperatury (gradientu):
  \( \int_L \frac{\alpha_t \Delta T(x)}{h} \bar{M}(x) dx \)
  Opisuje przemieszczenie spowodowane wygięciem elementu na skutek różnicy temperatur \(\Delta T\) między jego górną a dolną powierzchnią (na wysokości \(h\)).
  • \(h\) – wysokość przekroju poprzecznego.
  • \(\bar{M}(x)\) – wirtualny moment gnący od obciążenia jednostkowego.
• Wpływ osiadania podpór:
  \( \sum_i \delta_i \bar{r}_i \)
  Ten człon sumuje prace wirtualnych reakcji podporowych na rzeczywistych, znanych przemieszczeniach (osiadaniach) podpór. Jest to praca sił zewnętrznych.
  • \(\delta_i\) – znane przemieszczenie (liniowe lub kątowe) podpory \(i\) w stanie rzeczywistym.
  • \(\bar{r}_i\) – wartość reakcji na podporze \(i\) w stanie wirtualnym (od obciążenia jednostkowego).
• Wpływ podpór sprężystych (podatnych):
  \( \sum_i \frac{R_i \bar{r}_i}{k_i} \)
  Ten składnik uwzględnia energię odkształcenia zgromadzoną w podporach sprężystych.
  • \(R_i\) – wartość reakcji na podporze sprężystej \(i\) w stanie rzeczywistym.
  • \(\bar{r}_i\) – wartość reakcji na tej samej podporze w stanie wirtualnym.
  • \(k_i\) – sztywność podpory sprężystej \(i\) (np. w [kN/m] dla sprężyny liniowej).

Zalety i zastosowanie

Siła metody Maxwella-Mohra tkwi w jej wszechstronności i modulej budowie. Pozwala ona na obliczanie przemieszczeń w belkach, ramach i kratownicach, niezależnie od stopnia ich statycznej niewyznaczalności oraz od przyczyny tych przemieszczeń. Dzięki temu można analizować osobno wpływ każdego z czynników (obciążenia, temperatury, osiadania) i sumować efekty zgodnie z zasadą superpozycji.

Obliczanie całek Mohra, choć analitycznie możliwe, jest często upraszczane przez zastosowanie metody graficzno-analitycznej (reguły Wierieszczagina). Polega ona na mnożeniu pola powierzchni wykresu siły wewnętrznej z jednego stanu przez rzędną z drugiego wykresu, odczytaną pod środkiem ciężkości pierwszego. Dzięki temu skomplikowane obliczenia całkowe sprowadzają się do prostych operacji algebraicznych na polach figur geometrycznych.

Podsumowując, metoda Maxwella-Mohra jest eleganckim i skutecznym podejściem do analizy odkształceń. Jej oparcie na fundamentalnych zasadach energetycznych, uniwersalność zastosowań oraz możliwość uproszczenia obliczeń za pomocą reguły Wereszczagina czynią ją jednym z podstawowych i niezastąpionych narzędzi w edukacji i praktyce każdego inżyniera budownictwa.

Możliwość wyznaczenia przemieszczenia w dowolnym, konkretnym punkcie konstrukcji, bez konieczności wyznaczania równania całej linii ugięcia, czyni ją niezwykle efektywnym narzędziem w codziennej praktyce inżynierskiej.