Mechanika techniczna
Geometryczna niezmienność i statyczna wyznaczalność
- Geometryczna Niezmienność – Fundament Analizy Konstrukcji
- Słownik pojęć
- Reprezentacja podpór na schemacie kinematycznym
- Reprezentacja podpór na schemacie kinematyczny4. Warunek ilościowy geometrycznej niezmienności (warunek konieczny)
- Identyfikacja tarcz i więzów
- Warunek jakościowy (wystarczający) - podstawowe twierdzenia
-
Przykłady wyznaczania geometrycznej niezmienności
- Przykład 1
- Przykład 2
Geometryczna Niezmienność – Fundament Analizy Konstrukcji
Każda analiza konstrukcji inżynierskiej, niezależnie od jej złożoności czy metody obliczeniowej, musi rozpocząć się od odpowiedzi na jedno fundamentalne pytanie: czy badany ustrój jest stabilny? Geometryczna niezmienność to cecha układu, która gwarantuje, że pod wpływem dowolnego, ogólnego obciążenia doznaje on jedynie niewielkich odkształceń sprężystych, a nie przemieszczeń całego układu lub jego części jako mechanizmu. Układ, który tej cechy nie posiada, jest nazywany geometrycznie zmiennym lub chwiejnym i nie może być traktowany jako konstrukcja nośna.
Weryfikacja geometrycznej niezmienności jest zatem absolutnie kluczowym i pierwszym krokiem w analizie statycznej. Pozwala ona upewnić się, że schemat statyczny jest poprawny, zanim przystąpimy do czasochłonnych obliczeń sił wewnętrznych, reakcji czy przemieszczeń.Słownik pojęć
Aby mieć jasność o czym mówimy, przedstawiamy słownik pojęć:
Aby poprawnie analizować stabilność konstrukcji, musimy najpierw zdefiniować kilka fundamentalnych pojęć, które stanowią język opisu układów prętowych.
Tarcza
Tarcza (lub ciało sztywne) to wyidealizowany obiekt, zbiór punktów materialnych, w którym wzajemne odległości między dowolnymi dwoma punktami pozostają niezmienne, bez względu na działające siły. W analizie konstrukcji prętowych pojedynczy, sztywny pręt lub grupa prętów połączonych sztywnymi węzłami jest traktowana jako tarcza.
Stopień swobody
Stopień swobody to niezależny parametr geometryczny, którego zmiana opisuje zmianę położenia ciała lub układu ciał w przestrzeni. Liczba stopni swobody to minimalna liczba informacji, jaką musimy podać, aby jednoznacznie określić nowe położenie.
- Punkt swobodny na płaszczyźnie ma dwa stopnie swobody – dwa przemieszczenia liniowe (np. wzdłuż osi X i Y).
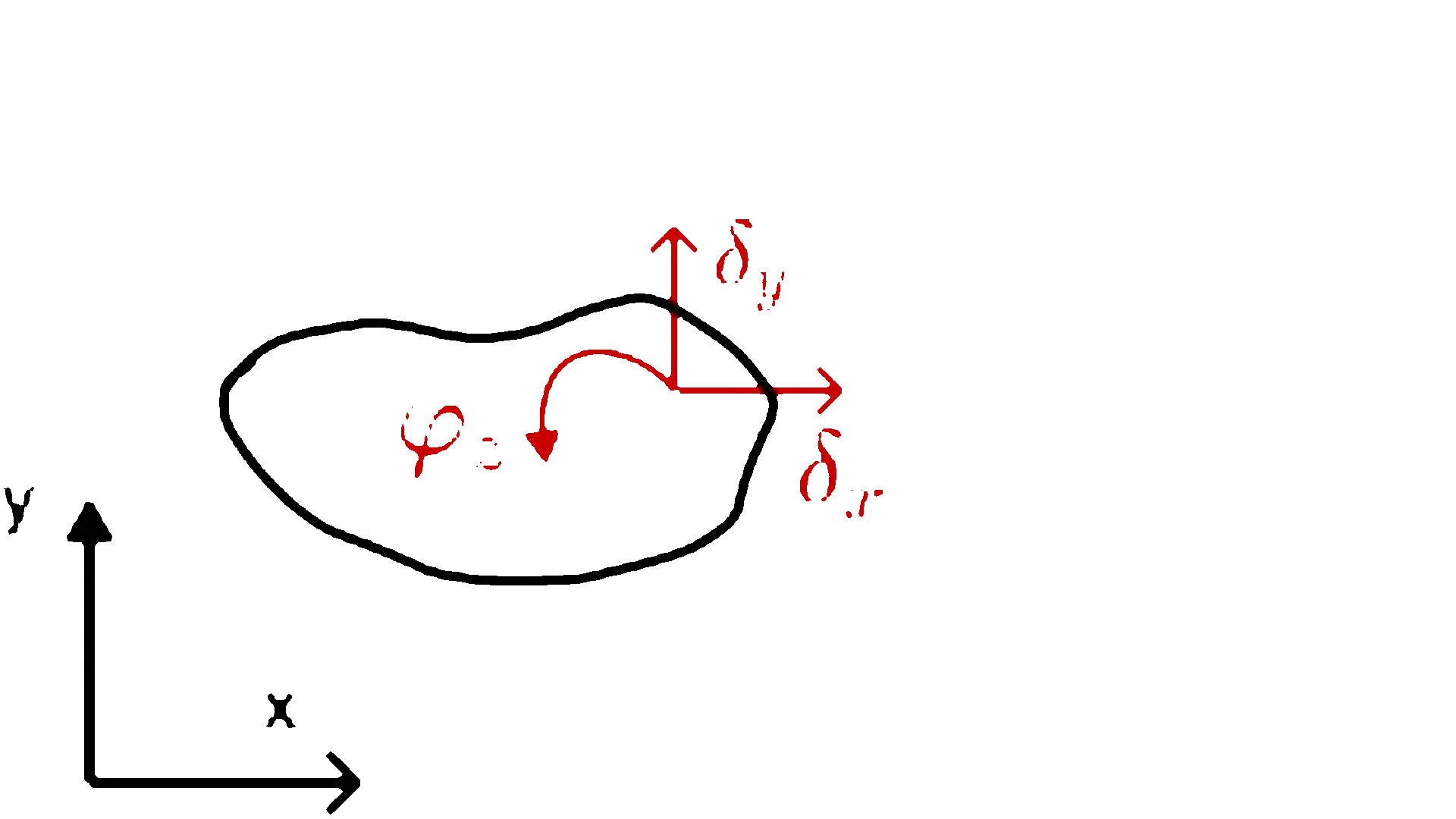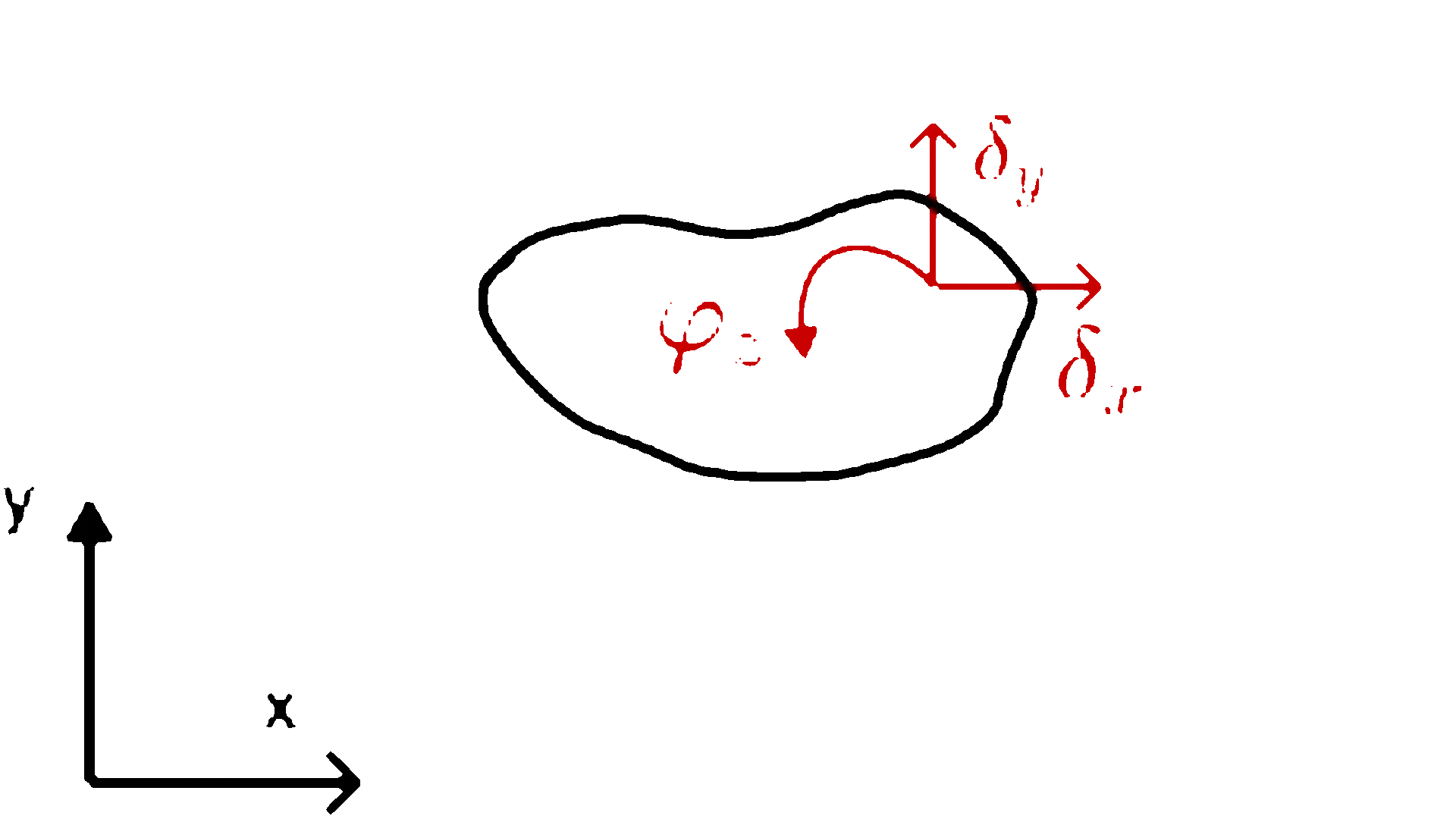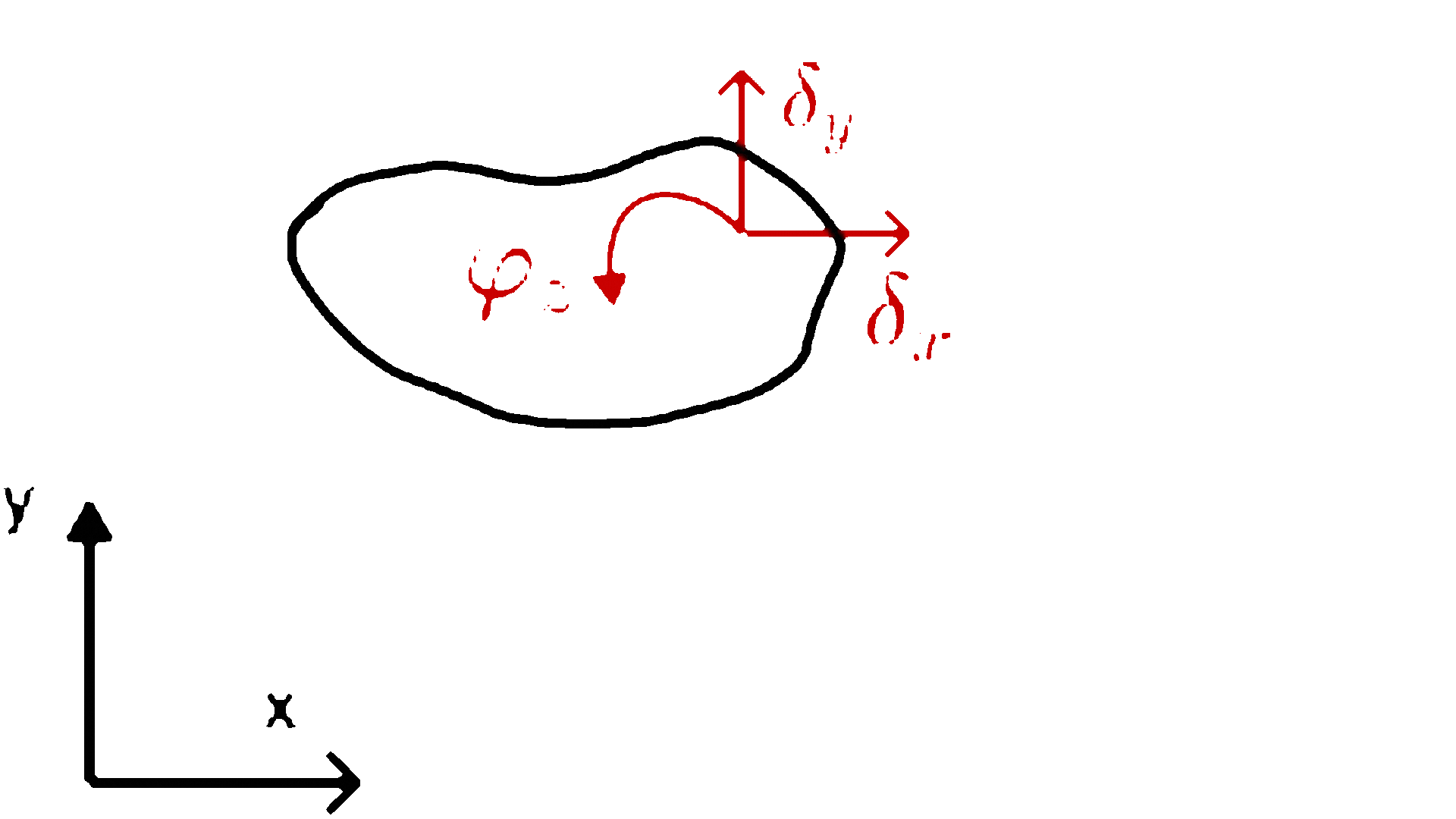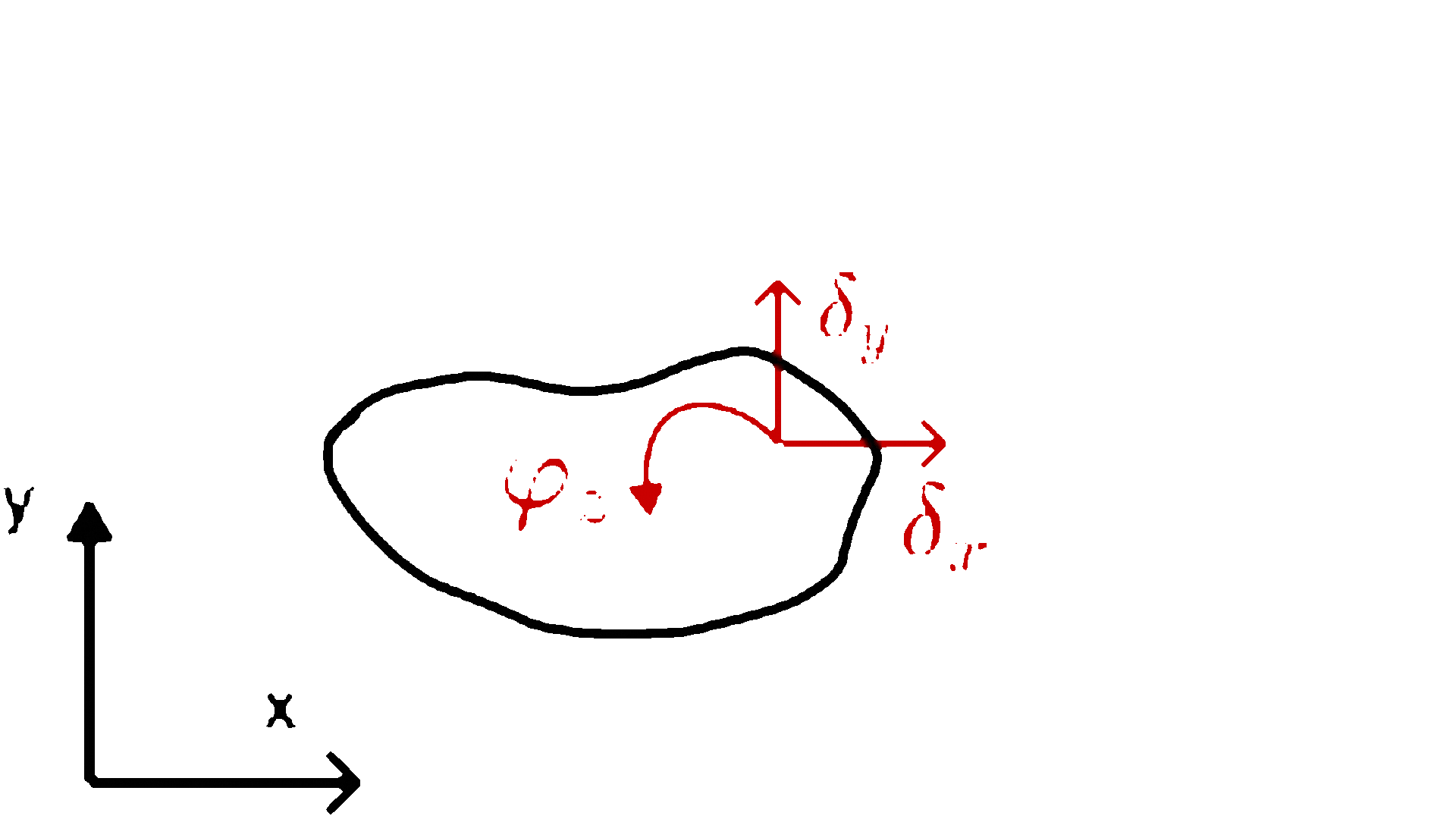
- Tarcza swobodna na płaszczyźnie ma trzy stopnie swobody. Aby określić jej położenie, wystarczy znać położenie jednego odcinka należącego do tej tarczy, co można opisać za pomocą dwóch współrzędnych jednego punktu i jednego kąta obrotu.
Tarcza podstawowa (fundament)
Tarcza podstawowa, zwana również ostoją lub fundamentem, jest szczególnym przypadkiem tarczy. Przyjmujemy, że jest ona naszym absolutnym układem odniesienia – jest idealnie nieruchoma, a więc pozbawiona wszystkich stopni swobody. To na niej opieramy konstrukcję i jej więzy elementarne.
Więź elementarna
Więź elementarna (lub więz prosty) to najprostszy, wyidealizowany model łącznika, który odbiera jeden stopień swobody. W mechanice jest nią najczęściej pręt prosty, połączony na obu końcach idealnymi przegubami.

Stopnie swobody i więzy w układach wielotarczowych
Rozszerzając te definicje na układy złożone:
- Układ składający się z \(t\) niezależnych tarcz na płaszczyźnie posiada łącznie \(3t\) stopni swobody.
- Przegub wewnętrzny, który łączy ze sobą \(t_i\) tarcz, sam w sobie odbiera pewną liczbę stopni swobody. Krotność takiego przegubu (\(k_i\)) określa, ile niezależnych obrotów jest możliwych w tym węźle i wynosi: \[ k_i = t_i - 1 \] Każdy taki przegub zastępuje pewną liczbę więzów elementarnych. Liczbę więzów zastępowanych przez przegub można obliczyć ze wzoru: \[ e_i = 2k_i = 2(t_i - 1) \]
- Na przykład przegub łączący dwie tarcze (\(t_i=2\)) zastępuje \(2(2-1)=2\) więzy elementarne. Natormiast przebug łączący tarcze o krotności \(k_i=3\) zastępuje \(2(3-1)=4\) więzy elementarne.
Na poniższym przykładzie widzimy układ z trzema tarczami (w tym tarcza (0) - fundament). Tarcze 1 i 2 połączone są z fundamentem, kazda za pomocą dwóch więzi elementarnych. Tarcze 1 i 2 połączone są ze sobą przegubem, który zastępuje dwa więzy elementarne.

Reprezentacja podpór na schemacie kinematycznym
Aby poprawnie zamodelować lub analizować układ, musimy wiedzieć jak reprezentować podpory na schemacie kinematycznym.
Rodzaje podpór w układzie płaskim
W tabeli dla przykładu podpora 2 i 3 są w wariantach przesuwnym w poziomie i pionie, ale podpora może być obrócona w dowolnym kierunku.
Tak samo podpora 5 i 6 są w wariantach przesuwnym w poziomie i pionie, ale podpora może być obrócona w dowolnym kierunku.
- 1. Podpora przegubowa nieprzesuwna - blokuje ruch punktu, nie blokuje obrotu
- 2. Podpora przegubowa przesuwna w poziomie - blokuje pionowy ruch punktu
- 3.Podpora przegubowa przesuwna w pionie - blokuje poziomy ruch punktu
- 4. Utwierdzenie pełne - blokuje ruch punktu i obrót - tarcza z takim podparciem jest nieruchoma (geometrycznie niezmienna)
- 5. Utwierdzenie z pionowym przesuwem - blokuje poziomy ruch oraz obrót - tarcza z takim podparciem może doznawać jedynie translacji (ruch liniowy) w kierunku pionowym
- 6. Utwierdzenie z poziomym przesuwem - blokuje pionowy ruch oraz obrót - tarcza z takim podparciem może doznawać jedynie translacji (ruch liniowy) w kierunku poziomym
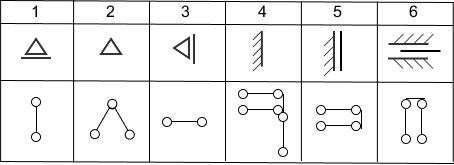
Reprezentacja podpór na schemacie kinematycznym. Warunek ilościowy geometrycznej niezmienności (warunek konieczny)
Pierwszym, najprostszym testem jest sprawdzenie relacji między liczbą więzów a liczbą stopni swobody układu. Dla układu płaskiego złożonego z t tarcz, całkowita liczba stopni swobody wynosi 3t. Jeśli liczba elementarnych więzów (wewnętrznych i zewnętrznych) wynosi w, to zachodzą następujące relacje:
- w < 3t – Układ jest geometrycznie zmienny GZ (chwiejny). Ma za mało więzów, aby go unieruchomić. Jest to mechanizm.
- w > 3t – Układ jest statycznie niewyznaczalny SN. Posiada więcej więzów niż to konieczne do unieruchomienia. Mimo to trzeba sprawdzić czy układ jest geometrycznie niezmienny GN.
- w = 3t – Układ jest statycznie wyznaczalny SW. Należy sprawdzić czy układ jest geometrycznie niezmienny GN?
Spełnienie relacji w do t jest warunkiem koniecznym, ale niewystarczającym. Oznacza to, że sama odpowiednia liczba więzów nie gwarantuje stabilności. Kluczowe jest ich prawidłowe rozmieszczenie.
Można się również spotkać z postacią warunku koniecznego, z którego obliczamy liczbę stopni swobody tarczy: \( lss=3t-2p-w \), gdzie:
- t - liczba tarcz (nie liczymy fundamentu)
- p - liczba przegubów wewnętrznych rzeczywistych
- w - liczba niezależnych więzów elementarnych (nie uwzględniamy więzów z przegubów wewnętrznych rzeczywistych)
Powyższy wzór jest równoważny z pierwszym który podaliśmy, po prostu zamiast zliczać więzy elementarne również z przegubów to liczymy te więzi przez wyrażenie \( 2p \).
Zliczanie więzów elementarnych
W tym momencie warto wspomnieć o zliczaniu więzów elementarnych, może zdarzyć się tak, że dwie więzi odbierają jednej tarczy ten sam stopień swobody, wtedy w zliczaniu więzów elementarnych trzeba uwzględnić tylko jedną więź.
Przykładem może być belka prosta bez przegubów podparta dwoma podporami przegubowymi nieprzesuwnymi (1). Wówczas mamy dwie więzi poziome, które blokują ten sam poziomy ruch poziomego pręta, w zliczaniu więzów elementarnych trzeba uwzględnić tylko jedną więź.
Przykład 1
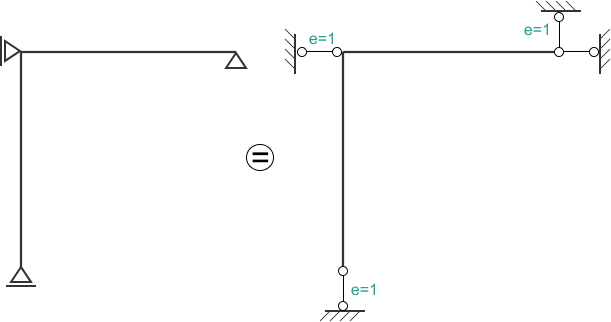
Tutaj podobnie jak dla belki prostej mamy 2 więzi poziome, które odbierają ten sam stopień swobody (ich kierunki się pokrywają i idą wzdłuż osi belki), w zliczaniu więzów elementarnych trzeba uwzględnić tylko jedną więź, a więc:
Liczba tarczy t=1
Liczba więzów w=3
Sprawdzam warunek konieczny \( w\geq 3t \)?
\( 3 = 3*1\) - układ jest statycznie wyznaczalny (SW)
Warto tutaj nadmienić, że występuje w takim przypadku
Mimo to da się narysować wykres momentów gnących i sił tnących dla takiego układu.
Przykład 2
Dla układu z "Rys. 2. Przykład układu z więziami elementarnymi i trzema tarczami", liczba więzów wynosi 6, a liczba tarcz t = 2 (nie liczymy fundamentu), więc w = 3t (6=3*2), więc układ jest statycznie wyznaczalny. W dalszej części sprawdzimy czy układ jest geometrycznie niezmienny.
Identyfikacja tarcz i więzów
Najpierw zidentyfikuj główne elementy belkowe/ramowe. Jeśli są połączone sztywnymi węzłami, traktuj je jako jedną, złożoną tarczę. Jeśli są połączone przegubami, rozdziel je w tych przegubach na osobne tarcze.
Ważne jest aby poprawnie zidentyfikować co jest "tarczą", a co "więzem".
Wewnętrzne pręty kratowe, które łączą dwie tarcze, to więzy wewnętrzne. Każdy taki pręt jest traktowany jako jeden elementarny więz, odbierający jeden stopień swobody.
Warto tutaj zwrócić szczególną uwagę na to w jaki sposób jest zaznaczony przegub wewnętrzny, ponieważ drobne różnice na rysunku mogą mieć istotny wpływ na klasyfikacje i podział tarcz i więzów wewnętrznych. Najlepiej jeśli pokażemy jakieś przykłady.
Przykład umieszczenia przegubu wewnętrznego w węźle.
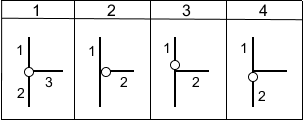
- 1) - przegub oddziela 3 osobne elementy, które mogą się obracać względem siebie
- 2) - przegub oddziela 2 osobne elementy - element pionowy 1 może się obracać względem elementu poziomego 2
- 3) - przegub oddziela 2 osobne elementy - element pionowy 1 może się obracać względem węzła sztywnego 2
- 4) - przegub oddziela 2 osobne elementy - węzeł sztywny 1 może się obracać względem pionowego elementu 2
Warunek jakościowy (wystarczający) - podstawowe twierdzenia
Twierdzenie o dwóch tarczach
Dwie tarcze połączone za pomocą trzech więzi elementarnych, które nie są ani równoległe, ani zbieżne, są geometrycznie niezmienne.
Przykłady dwóch tarcz które spełniają warunki twierdzenia
Przykład 1
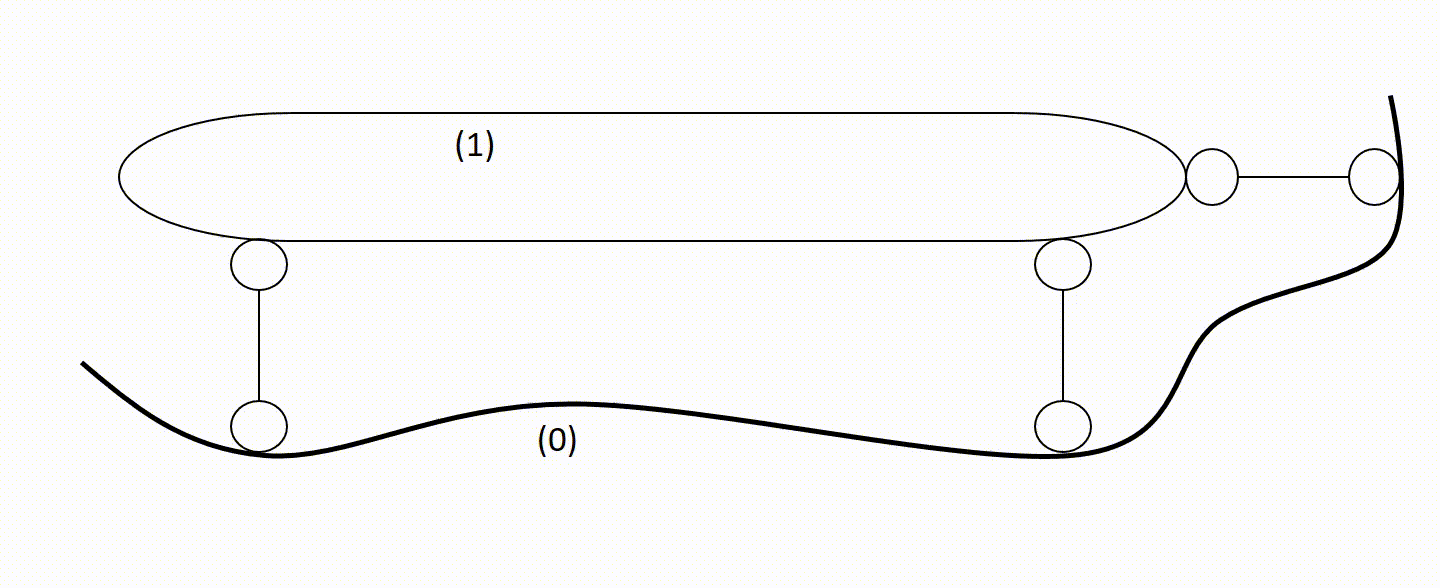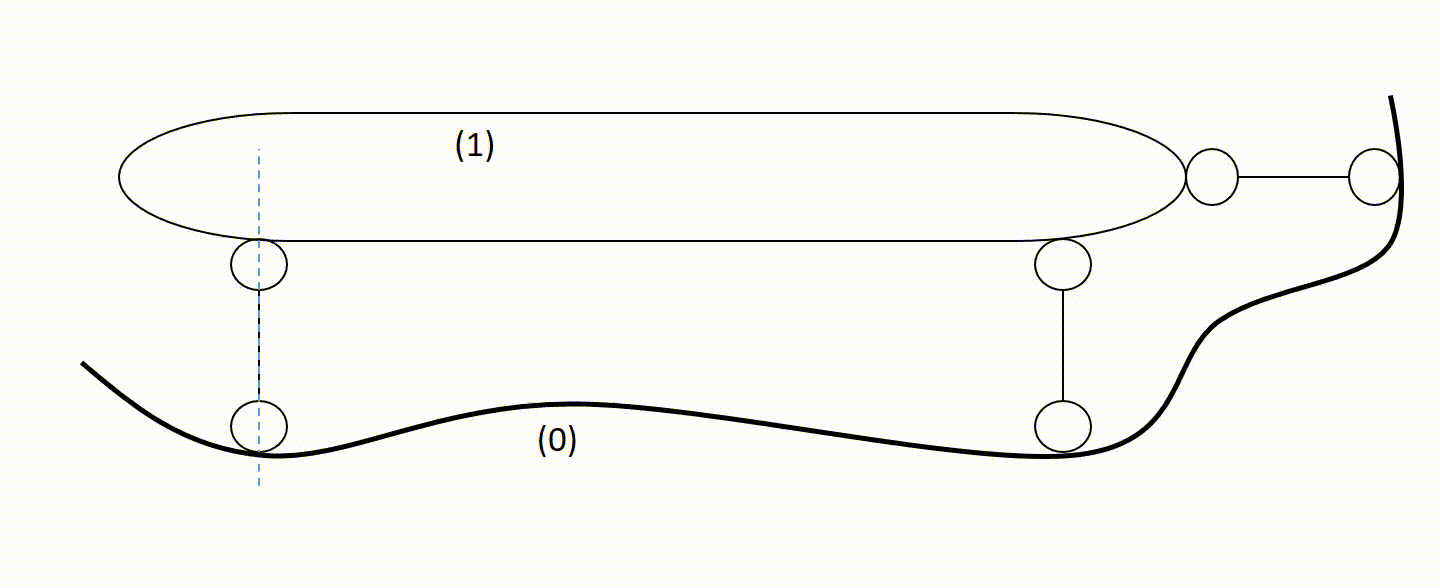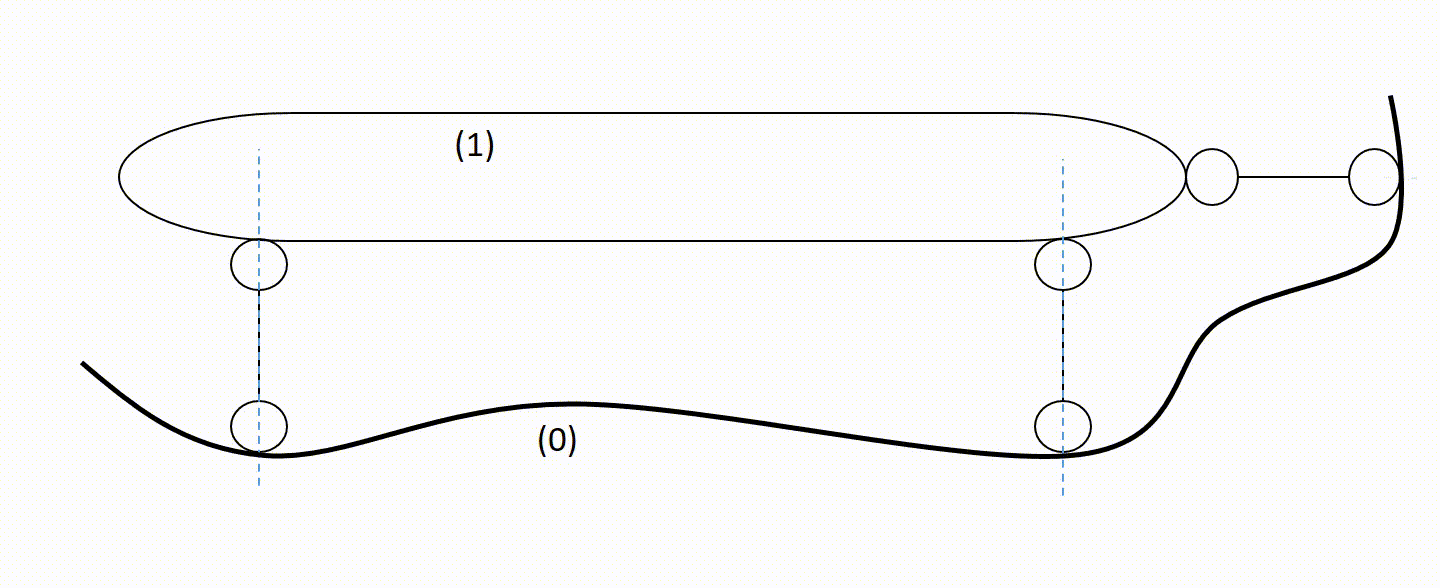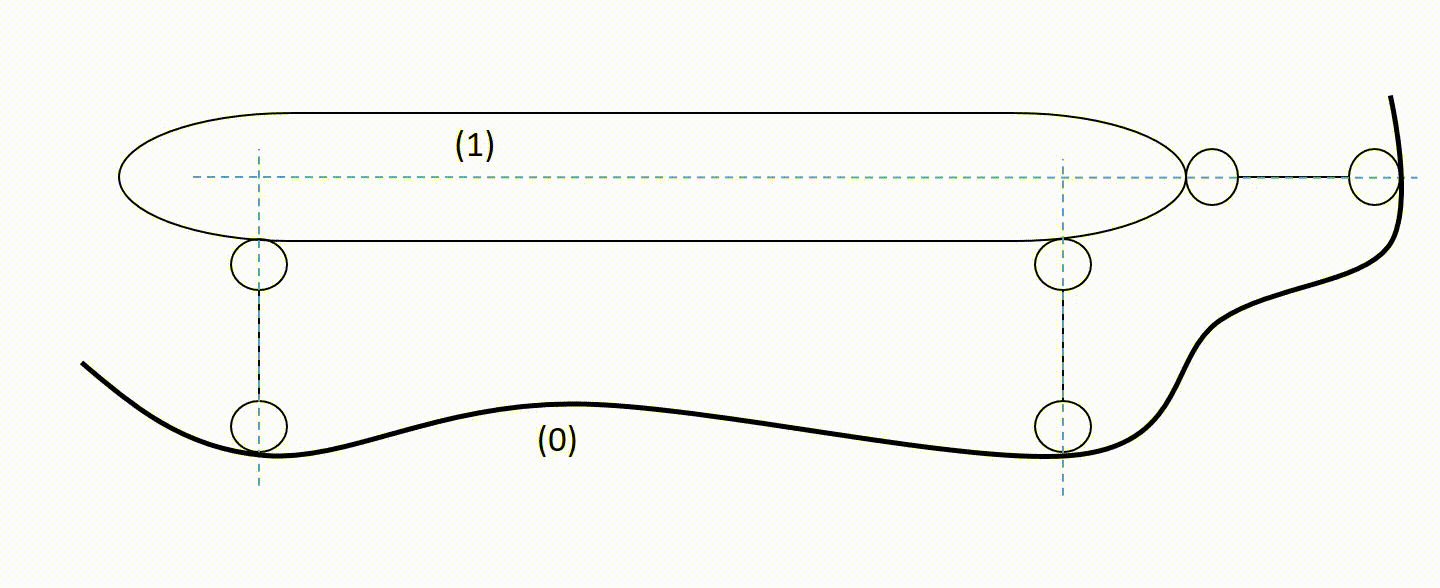
Na rysunku widzimy fundament (0) i tarcze (1) połączoną z fundamentem za pomocą trzech więzi elementarnych, które nie są ani równoległe, ani zbieżne, układ jest geometrycznie niezmienny.
Przykład 2
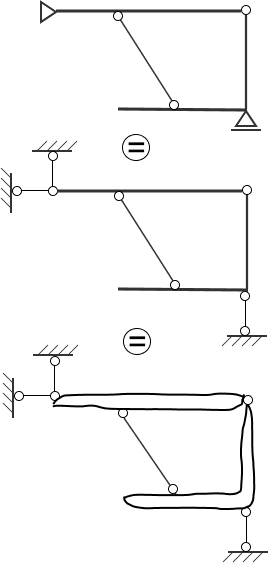
Na rysunku widzimy dwie tarcze połączone ze sobą przegubem (dwie więzi) i prętem (pojedyńczą więzią), a więc tarcze to połączenie spełnia warunki twierdzenia o dwóch tarczach i możemy je połączyć w jedną tarczę, a więc teraz widzimy to tak:

Teraz kolejny raz wykorzystując twierdzenie o dwóch tarczach, możemy połączyć to nową - supertarczę z fundamentem (tarczą podstawową) na podstawie tego samego twierdzenia (patrz rzykład 1 powyżej), a więc tym samym stwierdzić, że układ jest geometrycznie niezmienny.
Przykład zbyt małej liczby więzów tarczy
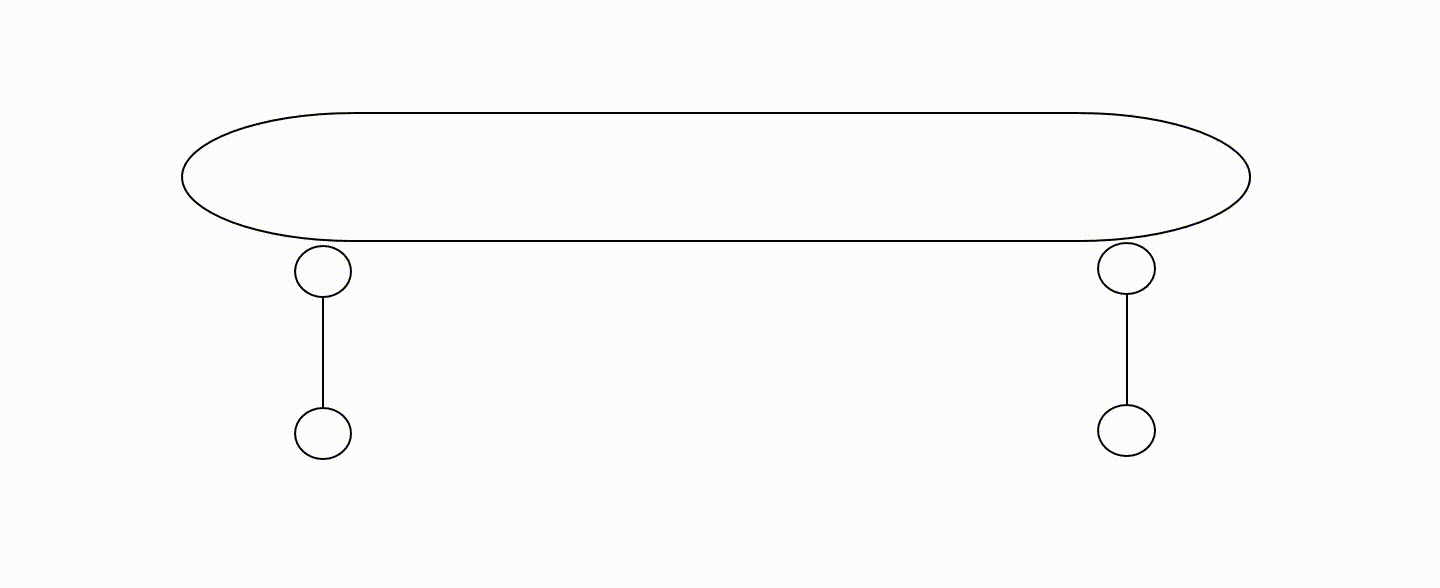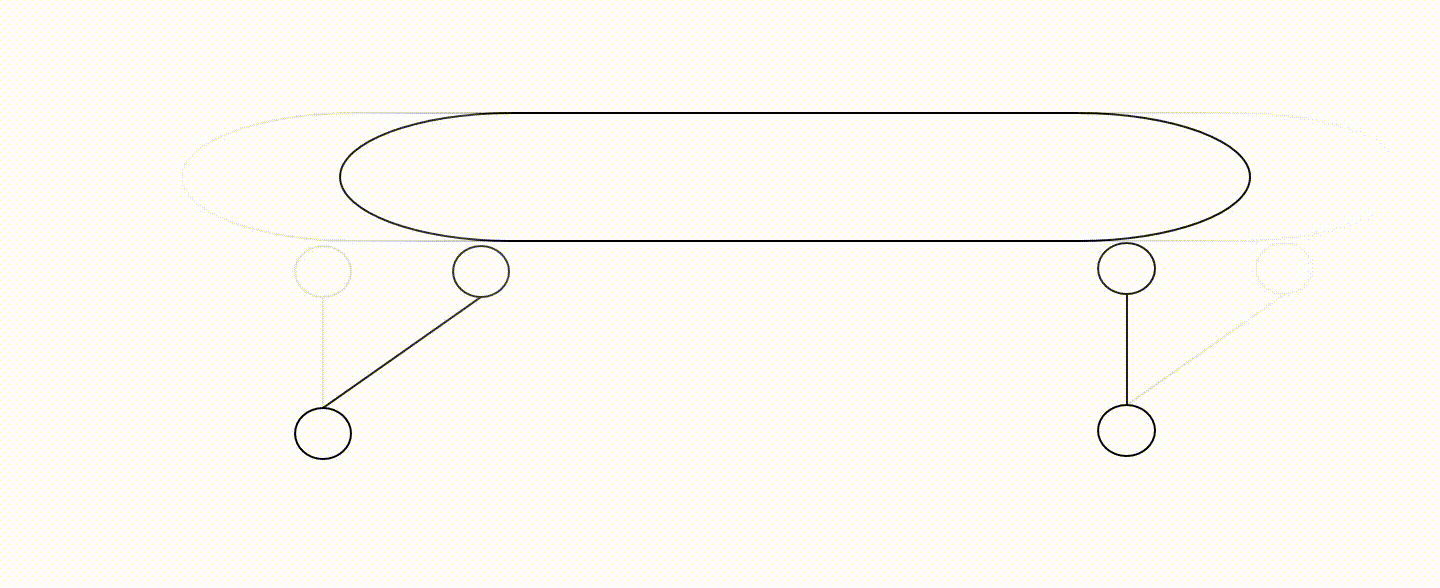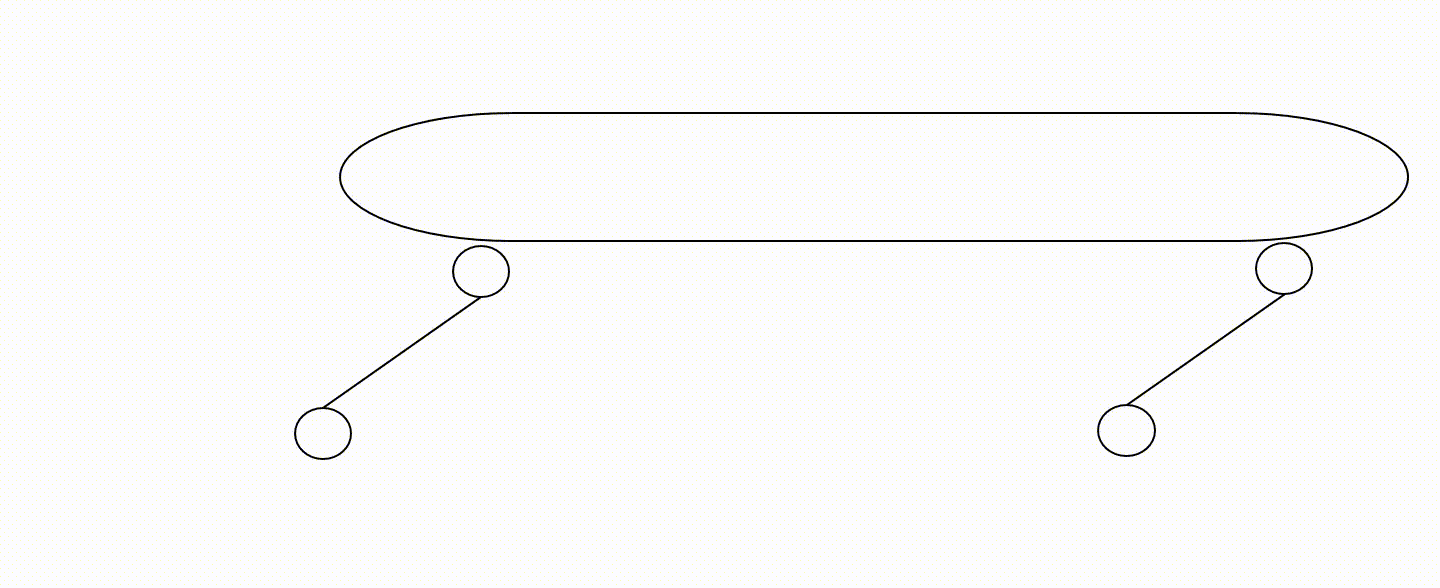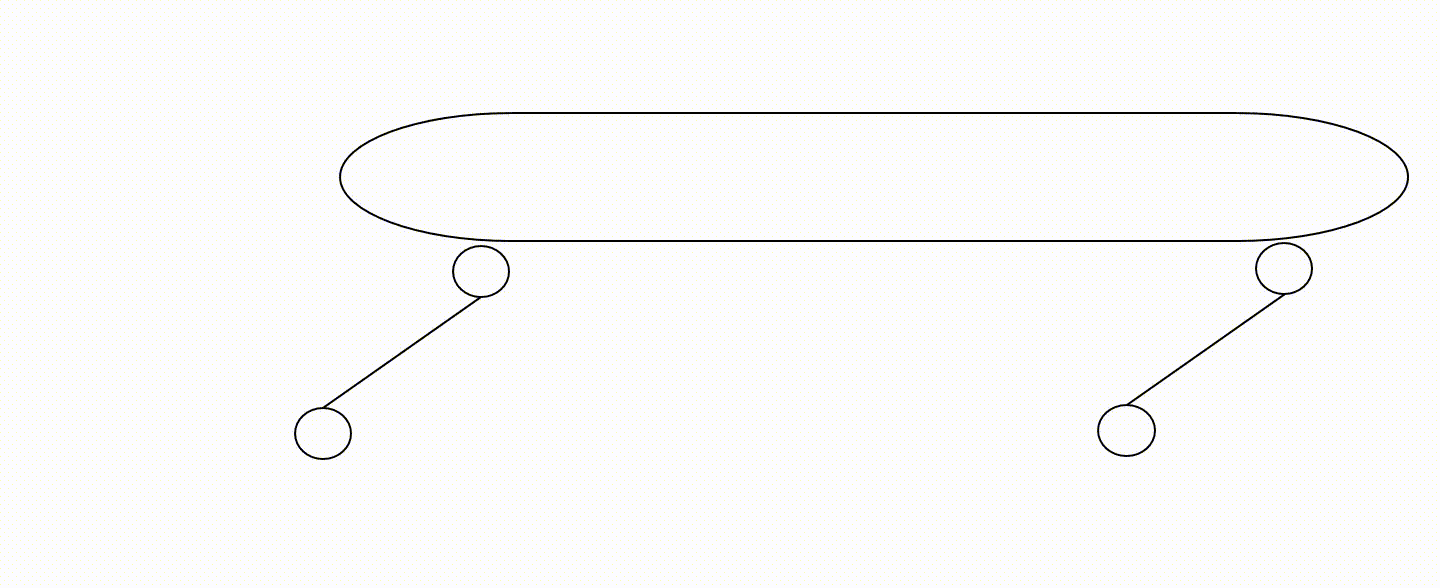
Przykład wadliwego rozmieszczenia więzów tarczy
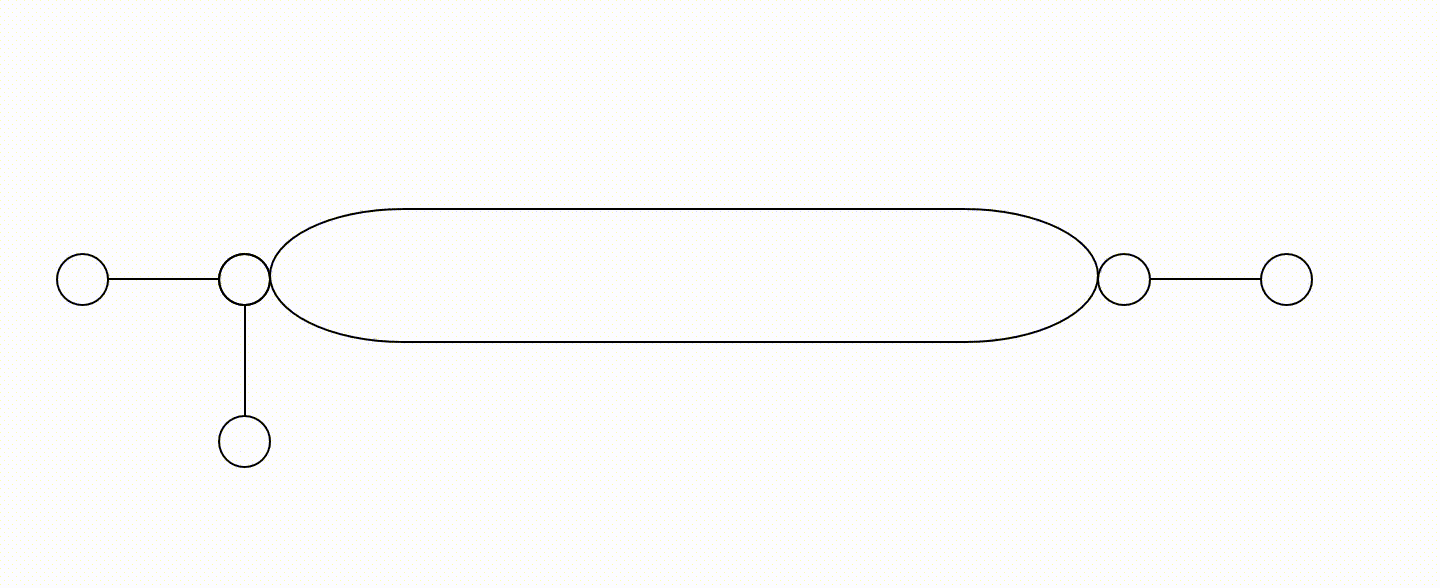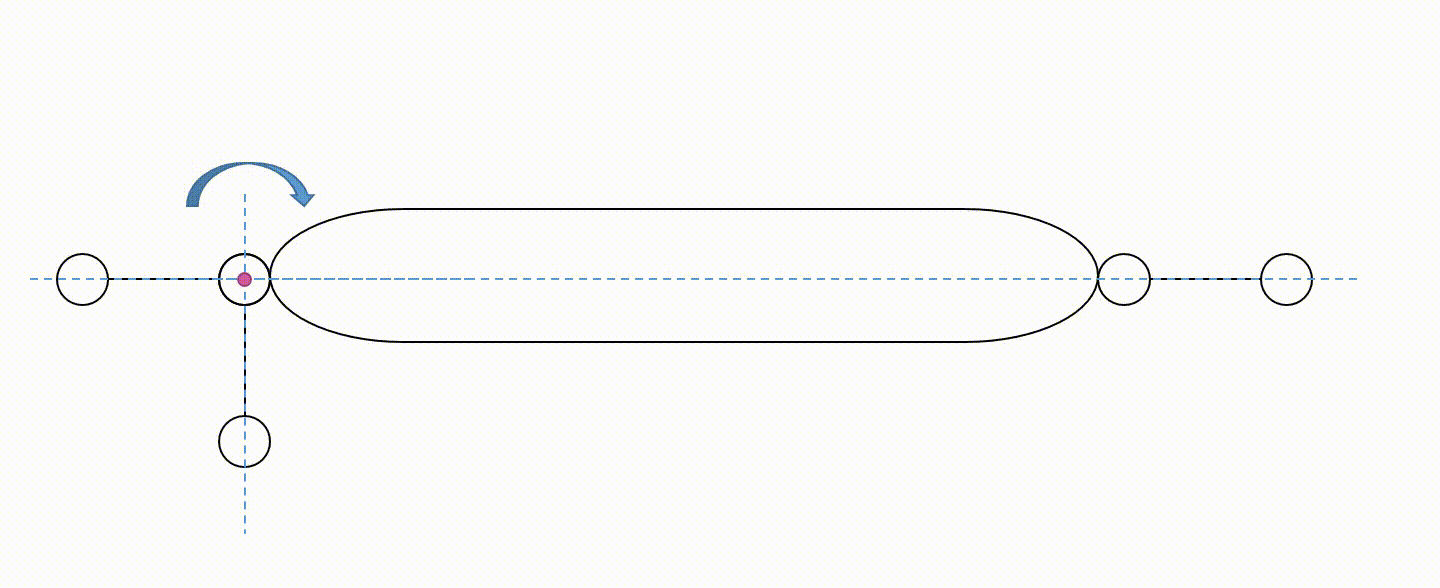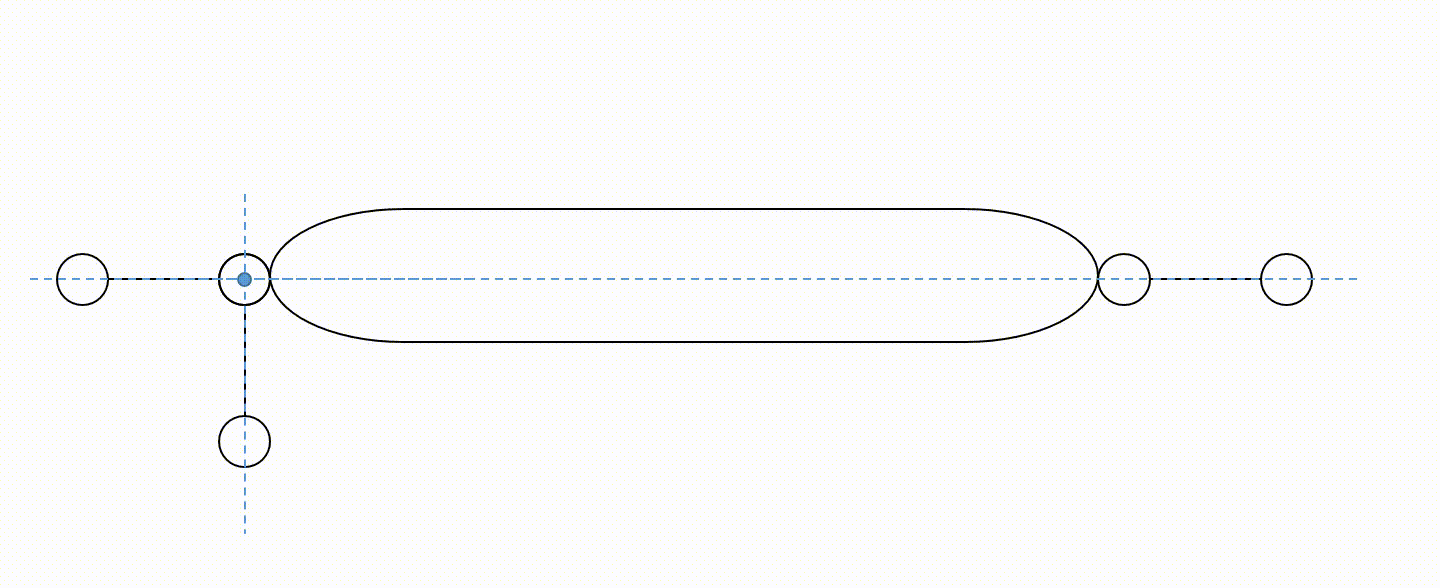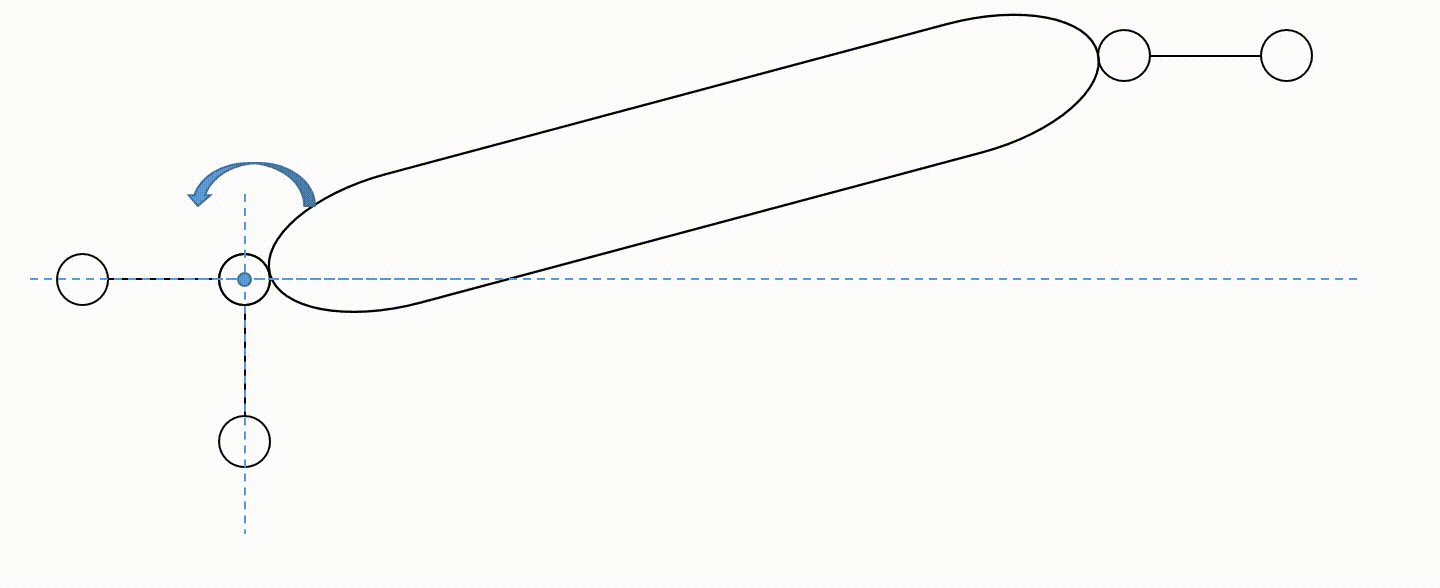
Na powyższych animacjach nie zaznaczono fundamentu (jest domyślnie).
Twierdzenie o trzech tarczach
Układ złożony z trzech tarcz, gdzie każda para tarcz połączona jest za pomocą dwóch więzi elementarnych tworzy jedną tarczę, jeżeli środki wzajemnego obrotu tych tarcz nie leżą na jednej prostej.
Przykłady trzech tarcz które spełniają warunki twierdzenia
Przykład 1
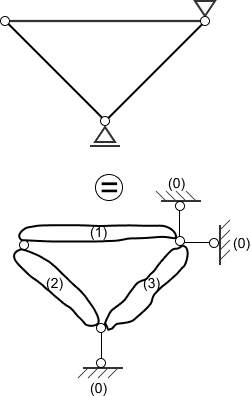
Na rysunku widzimy trzy tarcze (1,2,3) połączone ze sobą przegubami (dwie więzi). Tarcza 1 i 2 połączone dwiema więziami, tarcza 2 i 3 połączona dwoma więziami oraz tarcza 3 i 1 połączone dwoma więziami. Więzi te w przegubie kołowym się krzyżują, więc przeguby stanowią też o wzajemnych środkach obrotu tych tarcz wobec siebie. Te środki obrotu nie leżą na jednej linii, a więc to połączenie spełnia warunki twierdzenia o trzech tarczach i możemy je połączyć w jedną tarczę, a więc teraz widzimy to tak:
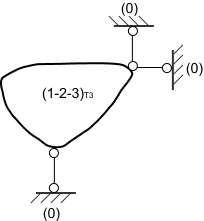
W tym momencie z twierdzenia o dwóch tarczach możemy połączyć supertarczę (1-2-3) z fundamentem (0) i stwierdzić, że układ jest geometrycznie niezmienny.
Geometryczna niezmienność układu złożonego
Zatem o układzie możemy powiedzieć, że jest geometrycznie niezmienny, jeśli na podstawie twierdzenia o dwóch tarczach (T2) i/lub twierdzenia o trzech tarczach (T3) jesteśmy w stanie połączyć wszystkie tarcze ze sobą i z fundamentem. Jeśli tego nie jesteśmy w stanie zrobić, to układ jest geometrycznie zmienny.
Przykłady wyznaczania geometrycznej niezmienności
Przykład 1
Sprawdzić statyczną wyznaczalność i geometryczną niezmienność belki
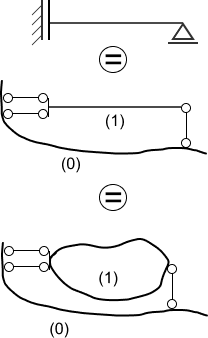
Liczba tarczy t=3
Liczba więzów w=3
Sprawdzam warunek konieczny \( w\geq 3t \)?
\( 3 = 3\cdot 1\) - układ jest statycznie wyznaczalny (SW), sprawdzamy czy układ jest geometrycznie niezmienny
Na rysunku widzimy tarczę podstawową (0) i tarczę (1) połączoną z tarczą podstawową za pomocą trzech więzi elementarnych, które nie są ani równoległe, ani zbieżne, układ jest geometrycznie niezmienny (twierdzenie o dwóch tarczach).
Przykład 2
Sprawdzić statyczną wyznaczalność i geometryczną niezmienność układu tarczowego
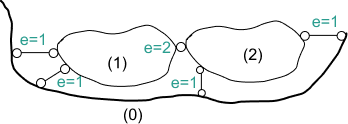
Liczba tarczy t=2 (nie liczymy fundamentu)
Liczba więzów w=6 (cztery podporowe i dwa z przegubu wewnętrznego)
Sprawdzam warunek konieczny \( w\geq 3t \)?
\( 6 = 3\cdot 2\) - układ jest statycznie wyznaczalny (SW), sprawdzamy czy układ jest geometrycznie niezmienny
Analiza kinematyczna
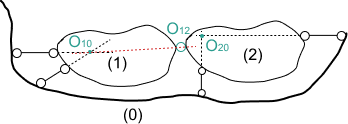
Na rysunku widzimy tarczę podstawową (0) i tarcze (1) i (2) połączone z tarczą podstawową za pomocą dwoch więzi elementarnych.
Wyznaczamy środki obrotu tarcz (1) i (2) i wykorzystujemy twierdzenie o trzech tarczach.
Układ złożony z trzech tarcz, gdzie każda para tarcz połączona jest za pomocą dwóch więzi elementarnych tworzy jedną tarczę, jeżeli środki wzajemnego obrotu tych tarcz nie leżą na jednej prostej.
Mamy trzy tarcze - (0) (1) (2)
- tarcze (0) i (1) są połączone za pomocą dwóch więzi elementarnych, zaznaczyliśmy na rysunku środek wzajemnego obrotu tarczy (1) względem tarczy (0) - \( O_{10} \)
- tarcze (1) i (2) są połączone za pomocą dwóch więzi elementarnych (przegub), środek wzajemnego obrotu tarczy (1) i tarczy (2) jest punktem tego przegubu - \( O_{12} \)
- tarcze (0) i (2) są połączone za pomocą dwóch więzi elementarnych, na rysunku zanaczyliśmy środek obrotu tarczy (2) względem tarczy (0) - \( O_{20} \)
Środki wzajemnego obrotu tarcz nie leżą na jednej prostej, co pokazaliśmy na rysunku czerwoną przerywaną linią, więc układ jest geometrycznie niezmienny.
Po więcej rozwiązanych przykładów zapraszamy do sekcji Zadań i Wideo.