Mechanika techniczna
Równowaga przestrzennego dowolnego układu sił
Statyka 3D Równowaga przestrzennego dowolnego układu sił
Przykładowe podpory
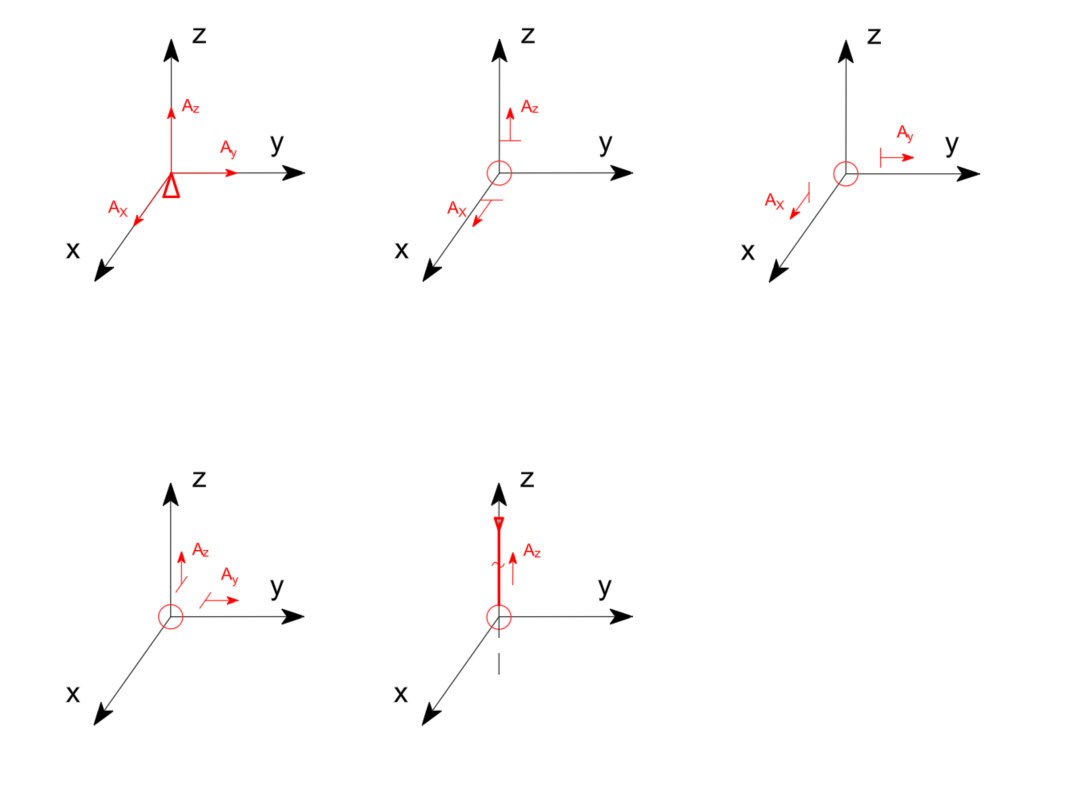
Równania równowagi
\begin{aligned} & \Sigma F_x=0 \\ & \Sigma F_y=0 \\ & \Sigma F_z=0 \\ & \Sigma M_x=0 \\ & \Sigma M_y=0 \\ & \Sigma M_z=0 \end{aligned}Przykład 1
Treść
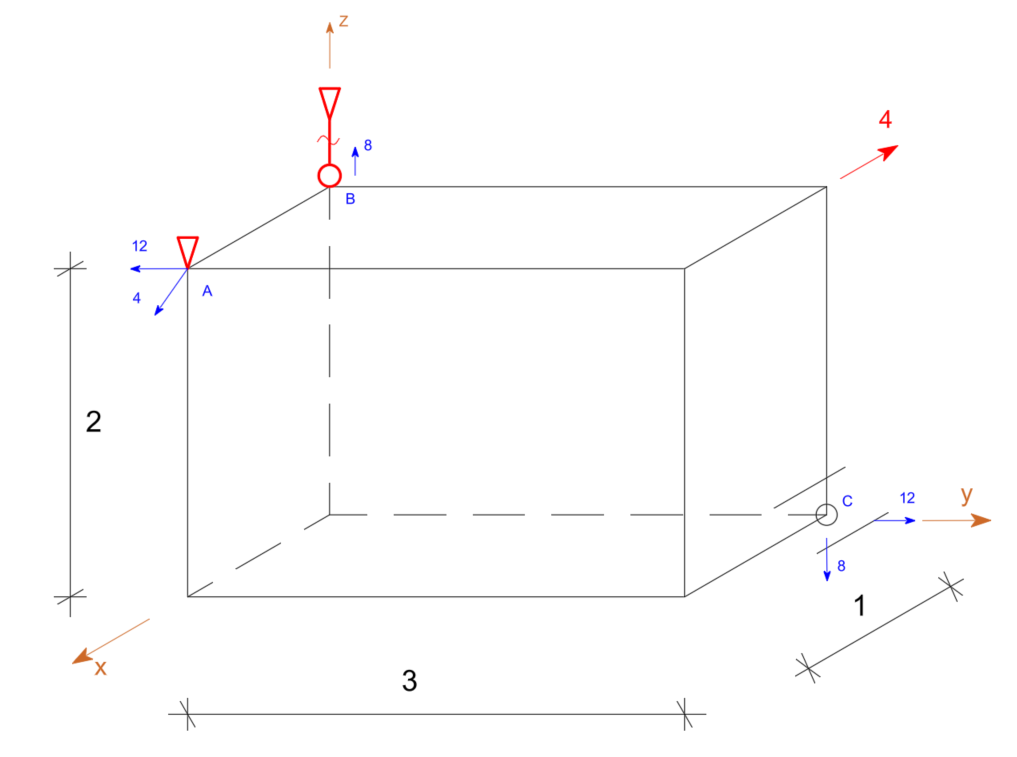
Dla podanego układu wyznacz reakcje
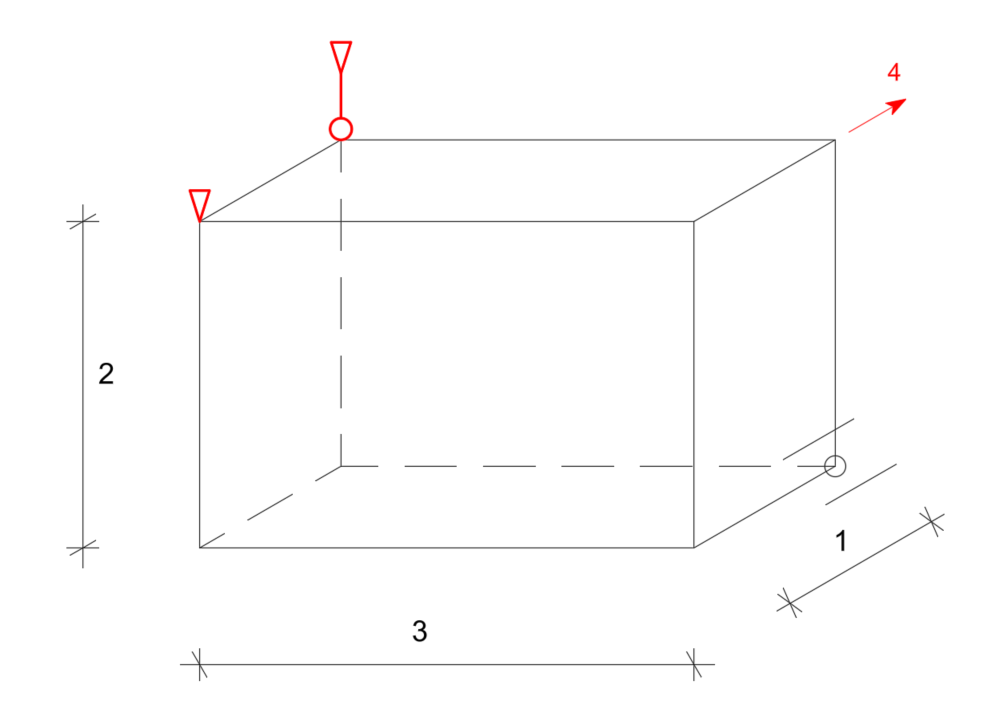
Rozwiązanie
Uwolnienie od więzów
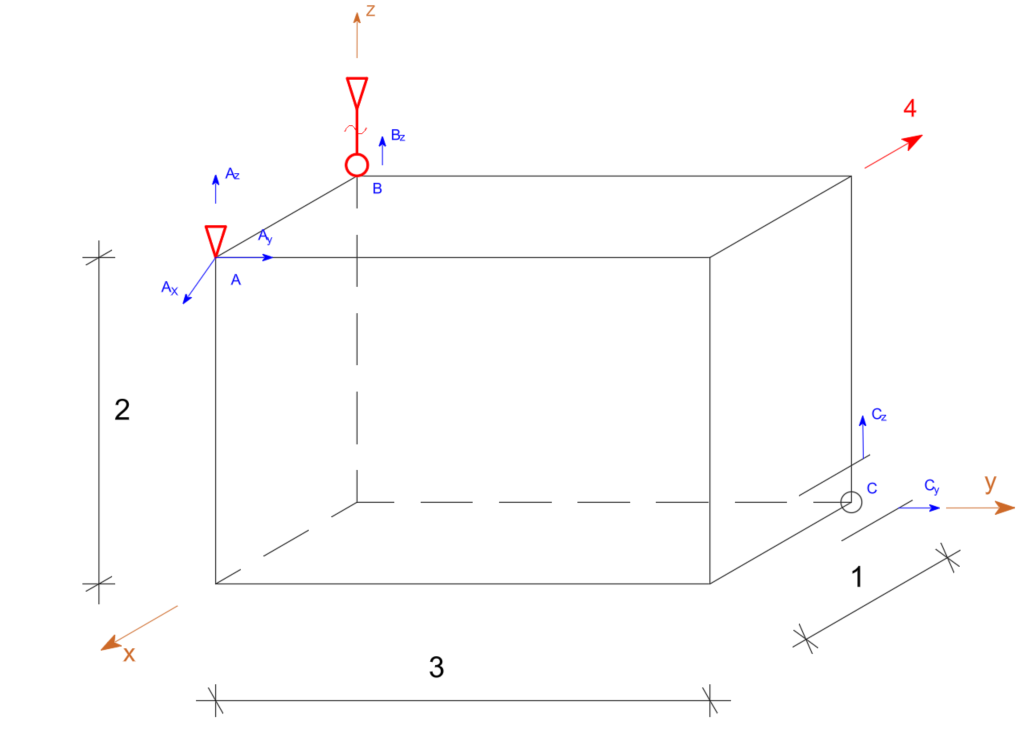
Suma rzutów na osi układu:
\begin{aligned} & \Sigma F_x=0 \quad A_x-4=0 \quad A_x=4 \\ & \Sigma F_y=0 \quad A_y+C_y=0 \\ & \Sigma F_z=0 \quad A_z+B_z+C_z=0 \\ & \end{aligned}Suma momentów względem osi X
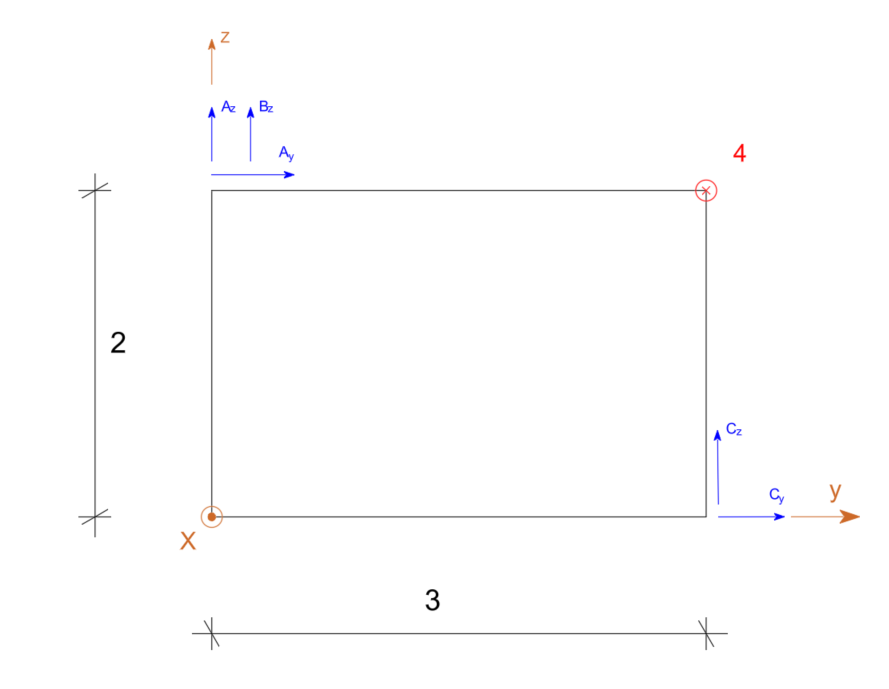 \begin{aligned}
\Sigma M_x=0 \quad C_z \cdot 3-A_y \cdot 2=0
\end{aligned}
\begin{aligned}
\Sigma M_x=0 \quad C_z \cdot 3-A_y \cdot 2=0
\end{aligned}
Suma momentów względem osi Y
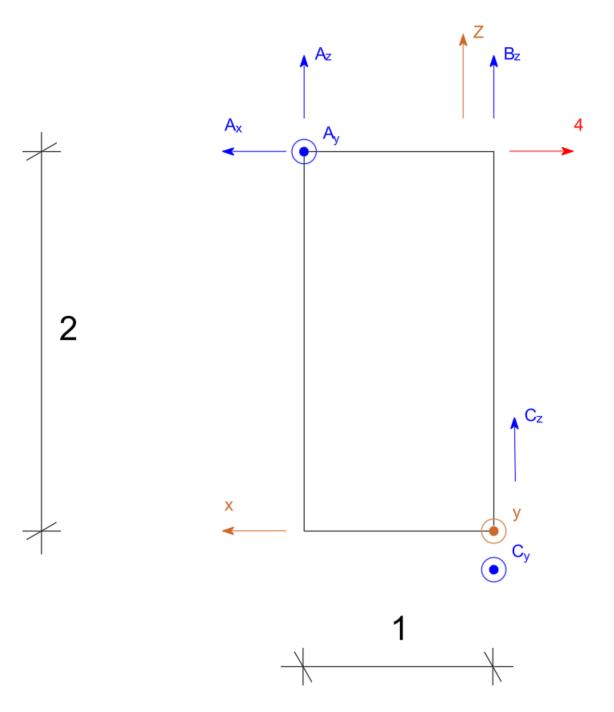 \begin{aligned}
\Sigma M_y=0 \quad-A_z \cdot 1+A_x \cdot 2-4 \cdot 2=0 \quad A_z=0
\end{aligned}
\begin{aligned}
\Sigma M_y=0 \quad-A_z \cdot 1+A_x \cdot 2-4 \cdot 2=0 \quad A_z=0
\end{aligned}
Suma momentów względem osi Z
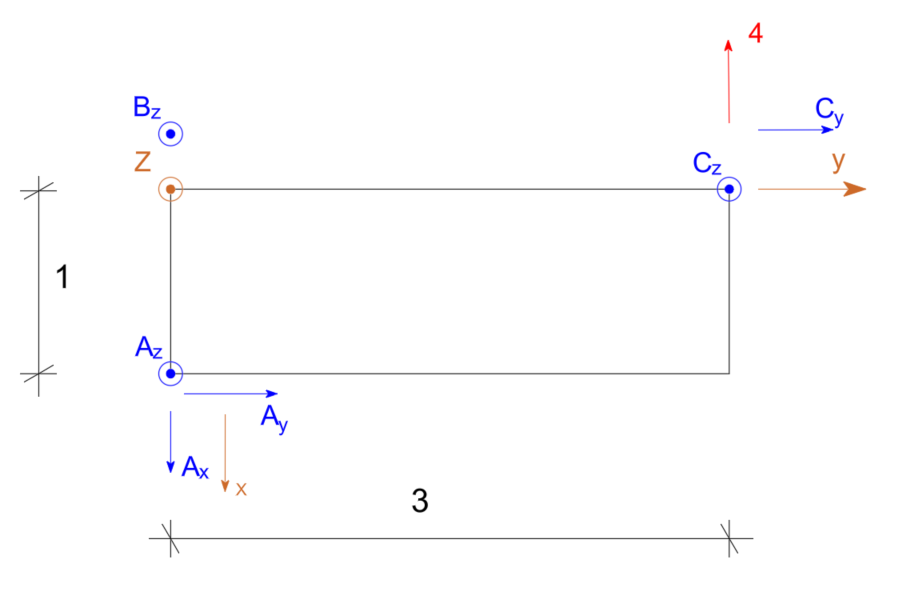 \begin{aligned}
\Sigma M_z=0 \quad A_y \cdot 1+4 \cdot 3=0 \quad A_y=-12
\end{aligned}
\begin{aligned}
\Sigma M_z=0 \quad A_y \cdot 1+4 \cdot 3=0 \quad A_y=-12
\end{aligned}
Podstawienie obliczonych wartości do poprzednich równań:
\begin{aligned} &C_z \cdot 3-A_y \cdot 2=0 \quad C_z=\frac{2}{3} A_y=-8\\ &A_y+C_y=0 \quad C_y=-A_y=12 \end{aligned}Zestawienie wyników