Wytrzymałość materiałów
Stateczność i wyboczenie
- Wprowadzenie – Stateczność jako fundamentalny warunek nośności
- Siła krytyczna i wzór Eulera – Analiza pręta idealnego
- Współczynnik długości wyboczeniowej
- Smukłość pręta i zakres stosowalności wzoru Eulera
- Wyboczenie niesprężyste – Pręty krępe i o średniej smukłości
- Wyprowadzenie wzoru Tetmajera-Jasińskiego
- Podejście normowe – Współczynnik wyboczeniowy
- Sprawdzenie stateczności pręta o różnych warunkach podparcia w dwóch płaszczyznach
- Przykład obliczeniowy - jednakowe warunki podparcia w dwóch płaszczyznach
- Przykład obliczeniowy - różne warunki podparcia w dwóch płaszczyznach
Wprowadzenie – Stateczność jako fundamentalny warunek nośności
W projektowaniu konstrukcji, zapewnienie, że element jest wystarczająco wytrzymały (tj. że naprężenia nie przekraczają wytrzymałości materiału), to tylko połowa sukcesu. Równie ważnym, a często decydującym, kryterium jest stateczność – czyli zdolność konstrukcji do utrzymania swojej pierwotnej formy równowagi pod działaniem obciążeń. Utrata stateczności, zwana wyboczeniem, to zjawisko, w którym osiowo ściskany, smukły pręt ulega nagłej i gwałtownej deformacji bocznej, mimo że naprężenia w nim mogą być znacznie niższe od granicy plastyczności materiału. Analiza stateczności jest zatem kluczowym elementem weryfikacji bezpieczeństwa i nośności, zwłaszcza w przypadku słupów, kolumn i innych elementów ściskanych.
Siła krytyczna i wzór Eulera – Analiza pręta idealnego
Pionierskie rozwiązanie problemu utraty stateczności podał Leonhard Euler w 1744 roku. Analizując idealnie prosty i osiowo obciążony pręt, doszedł do wniosku, że siła krytyczna nie zależy od wytrzymałości materiału, a jedynie od jego sztywności i geometrii. Dla podstawowego przypadku pręta przegubowo podpartego na obu końcach, siła krytyczna wyraża się słynnym wzorem:
\[ P_{kr} = \frac{\pi^2 EI_{min}}{L^2} \]gdzie \(E\) to moduł Younga, \(I_{min}\) to najmniejszy moment bezwładności przekroju, a \(l\) to długość pręta.
Aby uogólnić ten wzór na inne warunki podparcia (np. utwierdzenie-przegub, obustronne utwierdzenie), wprowadzono pojęcie długości wyboczeniowej (\(l_w\)):
\[ l_w = \mu \cdot L \] lub \[ l_w = \alpha \cdot L \]gdzie \(\mu\) / \(\alpha\) to współczynnik długości wyboczeniowej, zależny od sposobu podparcia pręta (np. dla pręta utwierdzono-wolnego \(\alpha=2\), a dla obustronnie utwierdzonego \(\alpha=0.5\)). Ostateczny, uniwersalny wzór Eulera ma postać:
\[ P_{kr} = \frac{\pi^2 EI_{min}}{L_w^2} \]Współczynnik długości wyboczeniowej
Współczynnik długości wyboczeniowej \(\alpha\) umożliwia przeliczenie długości pręta na długość wyboczeniową.
Wartości współczynników długości wyboczeniowej dla różnych warunków podparcia pręta są podane na Rys. 1.
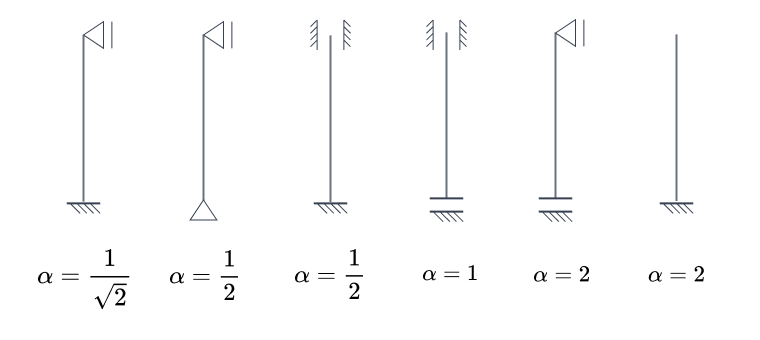
Jeśli mamy do czynienia z kratownicą, to współczynnik długości wyboczeniowej każdego pręta jest równy 1.
Warto tutaj dodać, że możemy się spotkać z nieco innym podparciem pręta, szczególnie jeśli analizujemy pręt "wyciągnięty" myślowo z ramy (analiza stateczności ramy, najczęściej w zadaniach z mechaniki budowli).
I tak na przykład należy mieć świadomość, że
- po pierwsze, co zdaje się być oczywiste, pręt po prostu może być "do góry nogami" względem tego co jest na rysunkach powyżej (współczynnik długości wyboczeniowej oczywiście pozostaje bez zmian),
- po drugie, co może być mniej oczywiste, blokady pionowe pręta (w sensie blokady w jego osi) mogą być albo na jednym brzegu, albo na drugim brzegu, albo na obu brzegach.
Prowadzi to do takich wniosków, że tożsame będą podparcia prętów na przykład takiego typu:
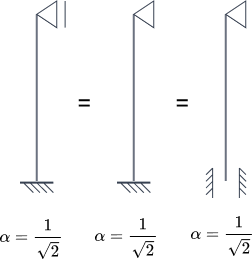
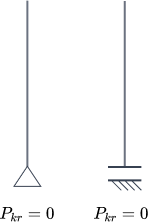
Na powyższym rysunku mamy pręt który na Rys1. jest przedstawiony jako pierwszy. Jest on podparty w trzech wariantach blokady ruchu pręta w jego osi 1) pionowa więź na dole, 2) pionowa więź na górze i na dole, 3) pionowa więź na górze.
W każdym przypadku traktujemy go tak samo w kontekście współczynnika długości wyboczeniowej.
Ma to zastosowanie do wszystkich typów prętów.
Możemy również spotkać przypadek (też najczęściej w kontekście analizy stateczności ramy i "wyciągania" z niej myślowo pręta), że wyciągnięty element jest niewystarczająco podparty, żeby był stabilny i z automatu można wówczas stwierdzić, że nie potrzeba żadnej siły krytycznej, żeby pręt nie był stabilny (Pkr=0).
Najprostszy przypadek to taki, że wystarczy, żeby pręt nie miał przynajmniej trzech więzi, wtedy na pewno nie jest stabilny.
Smukłość pręta i zakres stosowalności wzoru Eulera
Wzór Eulera opiera się na założeniu, że materiał pręta pracuje w zakresie sprężystym (zgodnie z prawem Hooke'a). Oznacza to, że naprężenie w momencie wyboczenia, zwane naprężeniem krytycznym (\(\sigma_{kr} = P_{kr}/A\)), nie może przekroczyć granicy proporcjonalności materiału (\(R_H\)).
Aby określić, czy pręt wyboczy się sprężyście, wprowadzono pojęcie smukłości pręta (\(\lambda\)), które jest miarą jego podatności na wyboczenie:
\[ \lambda = \frac{L_w}{i_{min}} \]gdzie \(i_{min}\) to najmniejszy promień bezwładności przekroju.
Wzór ten jest słuszny tylko dla prętów o dużej smukłości, dla których obliczone \(\sigma_{kr}\) jest mniejsze od \(R_H\). Istnieje pewna smukłość graniczna (\(\lambda_{gr}\)), powyżej której stosuje się wzór Eulera.
\[ \lambda_{gr} = \pi \sqrt{\frac{E}{R_H}} \]Wyboczenie niesprężyste – Pręty krępe i o średniej smukłości
Dla prętów krępych i o średniej smukłości (\(\lambda < \lambda_{gr}\)), naprężenie krytyczne obliczone ze wzoru Eulera byłoby większe od granicy proporcjonalności, co jest fizycznie niemożliwe. W tym zakresie wyboczenie następuje w sposób niesprężysty (sprężysto-plastyczny). Do opisu tego zjawiska stosuje się wzory empiryczne lub półempiryczne. Najbardziej znane to:
- Wzór Tetmajera-Jasińskiego: Aproksymuje on zachowanie materiału za pomocą prostej liniowej: \(\sigma_{kr} = a - b\lambda\), gdzie współczynniki \(a\) i \(b\) zależą od rodzaju materiału.
- Wzory Johnsona-Ostenfelda (paraboliczne): Używają krzywej parabolicznej do opisu zakresu niesprężystego.
Wyprowadzenie wzoru Tetmajera-Jasińskiego
Prosta Tetmajera-Jasińskiego jest liniową aproksymacją krzywej wyboczeniowej w zakresie niesprężystym. Jej ogólna postać to:
\[ \sigma_{kr} = a - b\lambda \]Aby wyznaczyć stałe materiałowe \(a\) i \(b\), wykorzystuje się dwa logiczne warunki brzegowe, które muszą być spełnione:
-
Warunek 1: Dla prętów bardzo krępych (\(\lambda \to 0\))
Gdy pręt jest bardzo krótki (krępy), nie ulega on wyboczeniu. Zniszczenie następuje przez uplastycznienie materiału. Oznacza to, że jego naprężenie krytyczne musi być równe granicy plastyczności \(R_e\). \[ \sigma_{kr}^{T-J} = R_e \quad \text{dla} \quad \lambda = 0 \quad \implies \quad a = R_e \] -
Warunek 2: Na granicy zakresów sprężystego i niesprężystego (\(\lambda = \lambda_{gr}\))
Prosta Tetmajera-Jasińskiego musi płynnie "łączyć się" z hiperbolą Eulera. W punkcie granicznym, czyli dla smukłości granicznej \(\lambda_{gr}\), wartość naprężenia krytycznego z obu wzorów musi być taka sama i równa granicy proporcjonalności \(R_H\). \[ \sigma_{kr}^{T-J} = R_H \quad \text{dla} \quad \lambda = \lambda_{gr} \quad \implies \quad R_H = a - b\lambda_{gr} \]
Podstawiając \(a = R_e\) do drugiego warunku, możemy wyznaczyć współczynnik \(b\):
\[ R_H = R_e - b\lambda_{gr} \implies b = \frac{R_e - R_H}{\lambda_{gr}} \]Pamiętając, że smukłość graniczna jest definiowana jako \( \lambda_{gr} = \pi \sqrt{\frac{E}{R_H}} \), możemy podstawić tę wartość do wzoru na \(b\). Ostatecznie, po wstawieniu wyznaczonych stałych \(a\) i \(b\) do równania prostej, otrzymujemy pełną postać wzoru Tetmajera-Jasińskiego:
\[ \sigma_{kr}^{T-J} = R_e - \frac{R_e - R_H}{\pi} \sqrt{\frac{R_H}{E}} \cdot \lambda \]Wzór ten obowiązuje dla prętów o smukłości w zakresie \(0 \le \lambda \le \lambda_{gr}\).
Korzystając z tego, że mamy już na wcześniejszym etapie zadania zawsze obliczoną smukłość graniczną
\[ \lambda_{\mathrm{gr}}=\pi \cdot \sqrt{\frac{\mathrm{E}}{\mathrm{R}_{\mathrm{H}}}} \]możemy zauważyć, że wyrażenie \(\frac{1}{\pi} \cdot \sqrt{\frac{\mathrm{R}_{\mathrm{H}}}{\mathrm{E}}}\) które stoi we wzorze na naprężenia jest odwrotnością smukłości granicznej, więc jest równe \(\frac{1}{\lambda_{\mathrm{gr}}}\) i wykorzystać je w formule na naprężenia i przekształcić wyprowadzoną wyżej postać
\[ \sigma_{\mathrm{kr}}^{\mathrm{TJ}}=\mathrm{R}_{\mathrm{e}}-\frac{\mathrm{R}_{\mathrm{e}}-\mathrm{R}_{\mathrm{H}}}{\pi} \cdot \sqrt{\frac{\mathrm{R}_{\mathrm{H}}}{\mathrm{E}}} \cdot \lambda \]do postaci:
\[ \sigma_{\mathrm{kr}}^{\mathrm{TJ}}=\mathrm{R}_{\mathrm{e}}-\frac{\mathrm{R}_{\mathrm{e}}-\mathrm{R}_{\mathrm{H}}}{\lambda_{\mathrm{gr}}} \cdot \lambda \]a jeśli byśmy chcieli od razu policzyć siłę krytyczną to możemy przekształcić wzór
\[ \sigma_{\mathrm{kr}}=\frac{\mathrm{P}_{\mathrm{kr}}}{\mathrm{~A}}=>\mathrm{P}_{\mathrm{kr}}=\sigma_{\mathrm{kr}} \cdot \mathrm{~A} \]i wówczas siła krytyczna według wzoru Tetmajera-Jasińskiego:
\[ \mathrm{P}_{\mathrm{kr}}=\mathrm{A} \cdot\left(\mathrm{R}_{\mathrm{e}}-\frac{\mathrm{R}_{\mathrm{e}}-\mathrm{R}_{\mathrm{H}}}{\lambda_{\mathrm{gr}}} \cdot \lambda\right) \]Podejście normowe – Współczynnik wyboczeniowy
W praktyce inżynierskiej, zwłaszcza w projektowaniu według norm (np. Eurokodów), powyższe teorie są uproszczone do postaci jednego współczynnika wyboczeniowego (\(\chi\)). Współczynnik ten (\(\chi \le 1\)) jest współczynnikiem redukcyjnym, który uwzględnia wpływ smukłości pręta, jego imperfekcji (początkowych niedoskonałości geometrycznych) oraz rodzaju przekroju. Nośność obliczeniowa elementu ściskanego jest wtedy wyznaczana jako iloczyn nośności przekroju na ściskanie i tego właśnie współczynnika, co w prosty sposób uwzględnia ryzyko utraty stateczności.
Sprawdzenie stateczności pręta o różnych warunkach podparcia w dwóch płaszczyznach
W dotychczasowych rozważaniach zakładaliśmy, że warunki podparcia pręta są takie same w każdej płaszczyźnie zginania. W praktyce inżynierskiej, szczególnie w konstrukcjach szkieletowych, bardzo często mamy do czynienia z sytuacją, w której element (np. słup) jest podparty w jeden sposób w płaszczyźnie ramy, a w zupełnie inny w płaszczyźnie prostopadłej. Prowadzi to do konieczności przeprowadzenia dwóch niezależnych analiz stateczności, aby znaleźć rzeczywistą, najmniejszą siłę krytyczną.
Dwie płaszczyzny, dwie analizy
Element konstrukcyjny zawsze "wybierze" najłatwiejszą drogę do utraty stateczności – czyli wyboczy się w tym kierunku, w którym jego odporność na wyboczenie jest najmniejsza. Odporność ta zależy od dwóch czynników: sztywności giętnej (\(EI\)) i długości wyboczeniowej (\(L_w\)). Ponieważ przekrój ma zazwyczaj dwie osie głównych momentów bezwładności (\(I_y\) i \(I_z\)), a warunki podparcia mogą definiować dwie różne długości wyboczeniowe, musimy rozpatrzyć dwa możliwe scenariusze wyboczenia:
- Wyboczenie w płaszczyźnie XZ: Obrót następuje wokół osi Y. Analizujemy warunki podparcia "widziane" w tej płaszczyźnie, aby określić długość wyboczeniową \(L_{w,XZ}\).
- Wyboczenie w płaszczyźnie XY: Obrót następuje wokół osi Z. Analizujemy warunki podparcia "widziane" w tej płaszczyźnie, aby określić długość wyboczeniową \(L_{w,XZ}\).
Algorytm postępowania
Aby poprawnie wyznaczyć siłę krytyczną dla takiego pręta, należy postępować według następującego algorytmu:
-
Analiza wyboczenia wokół osi Y (w płaszczyźnie XZ):
- Określ warunki podparcia w tej płaszczyźnie i znajdź odpowiedni współczynnik \(\alpha_{XZ}\).
- Oblicz długość wyboczeniową: \(L_{w,XZ} = \alpha{XZ} \cdot L\).
- Oblicz smukłość pręta dla tej płaszczyzny: \(\lambda_{XZ} = \frac{L_{w,XZ}}{i_y}\), gdzie \(i_y = \sqrt{I_y/A}\).
- Na podstawie smukłości \(\lambda_{XZ}\), oblicz naprężenie krytyczne \(\sigma_{kr,XZ}\) (korzystając ze wzoru Eulera lub Tetmajera-Jasińskiego).
- Oblicz siłę krytyczną dla tej płaszczyzny: \(P_{kr,XZ} = \sigma_{kr,XZ} \cdot A\).
- Lub ze wzoru Eulera \(P_{kr,XZ} = \frac{\pi^2 EI_y}{L_{w,XZ}^2}\).
-
Analiza wyboczenia wokół osi Z (w płaszczyźnie XY):
- Określ warunki podparcia w tej płaszczyźnie i znajdź odpowiedni współczynnik \(\alpha_{XY}\).
- Oblicz długość wyboczeniową: \(L_{w,XY} = \alpha_{XY} \cdot L\).
- Oblicz smukłość pręta dla tej płaszczyzny: \(\lambda_{XY} = \frac{L_{w,XY}}{i_z}\), gdzie \(i_z = \sqrt{I_z/A}\).
- Na podstawie smukłości \(\lambda_{XY}\), oblicz naprężenie krytyczne \(\sigma_{kr,XY}\).
- Oblicz siłę krytyczną dla tej płaszczyzny: \(P_{kr,XY} = \sigma_{kr,XY} \cdot A\).
- Lub ze wzoru Eulera \(P_{kr,XY} = \frac{\pi^2 EI_z}{L_{w,XY}^2}\).
-
Wyznaczenie rzeczywistej siły krytycznej:
Ostateczna, rzeczywista siła krytyczna dla całego pręta jest najmniejszą z wartości obliczonych dla obu płaszczyzn:
\[ P_{kr} = \min(P_{kr,XZ}, P_{kr,XY}) \]Konstrukcja zawiedzie przez utratę stateczności w tym kierunku, dla którego siła krytyczna jest niższa.
Przykład obliczeniowy - jednakowe warunki podparcia w dwóch płaszczyznach
Treść
Dany jest pręt o długości 2m podparty przegubowo na obu końcach, o przekroju prostokątnym 10x15cm.
Dane materiałowe: E=210 GPa, Re=215 MPa, RH=200 MPa.
Oblicz siłę krytyczną dla tego pręta.
Rozwiązanie
Rozwiązanie pochodzi z kalkulatora na naszej stronie -> Kalkulator Stateczności Osiowo Ściskanych Prętów <- .



Gdyby pręt miał większą długość (i tym samym by był bardziej smukły) wówczas smukłość pręta mogłaby być większa od granicznej i konieczne by było wykorzystanie wzoru Eulera.
Przykładowo dla pręta o długości 4m i tych samych pozostałych parametrach smukłość pręta wynosiłaby: \( \lambda = 138.6 \) i byłaby większa od granicznej, wówczas siła krytyczna ze wzoru Eulera
\begin{aligned} & P_{k r}=\frac{\pi^2 \cdot E \cdot J_{\min }}{l_w^2} \\ & P_{k r}=\frac{\pi^2 \cdot 210 \cdot 10^9 \cdot 1250.00 \cdot 10^{-8}}{4.000^2} \cdot 10^{-3}=1619.2 \mathrm{kN} \end{aligned}Przykład obliczeniowy - różne warunki podparcia w dwóch płaszczyznach
Treść
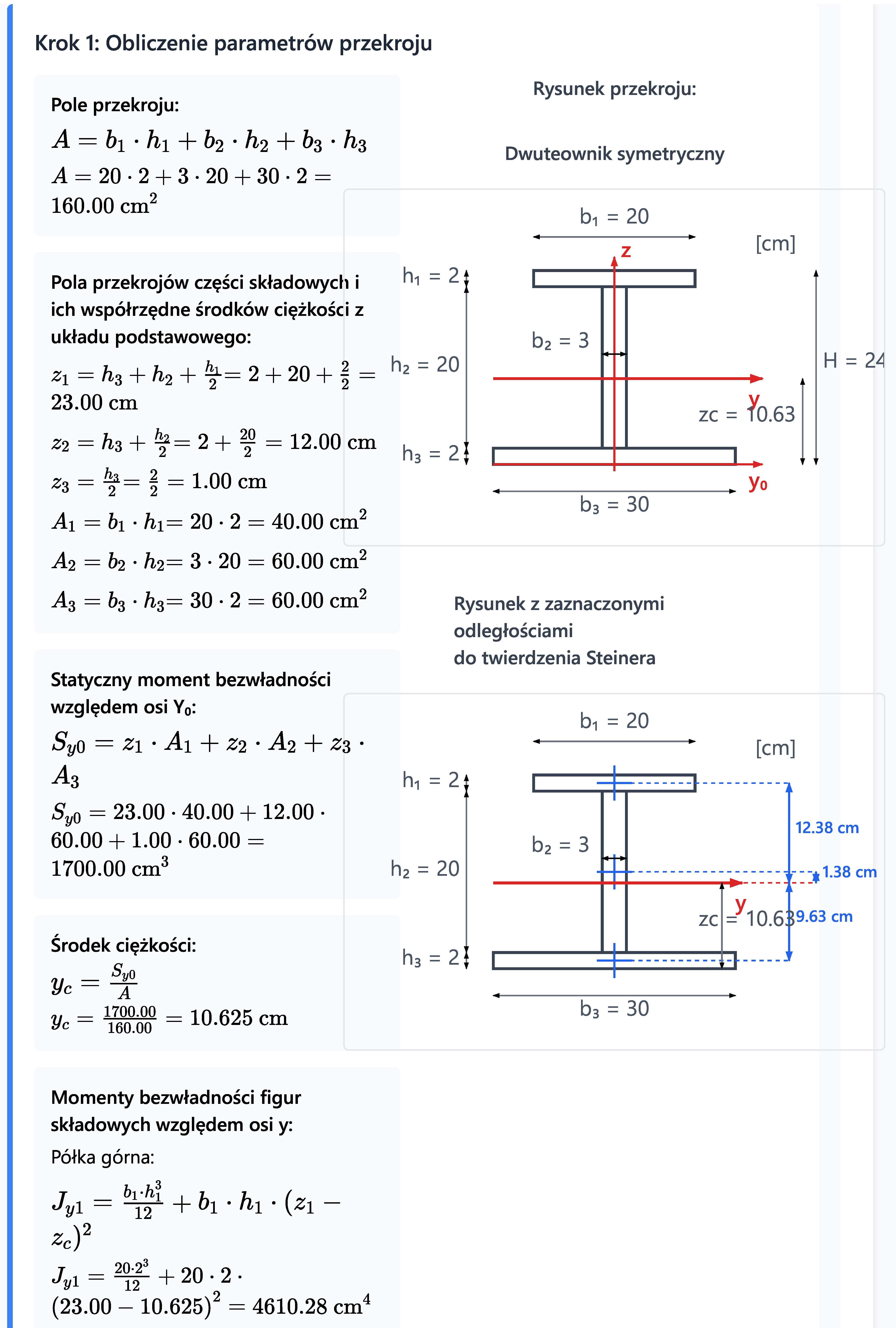
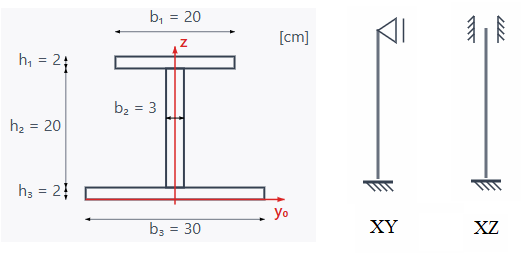
Dany jest pręt o długości 12m o przekroju dwuteowym oraz o różnym schemacie podparcia w dwóch płaszczyznach, jak na rysunku poniżej.
Dane materiałowe: E=195 GPa, Re=215 MPa, RH=200 MPa.
Oblicz siłę krytyczną dla tego pręta.
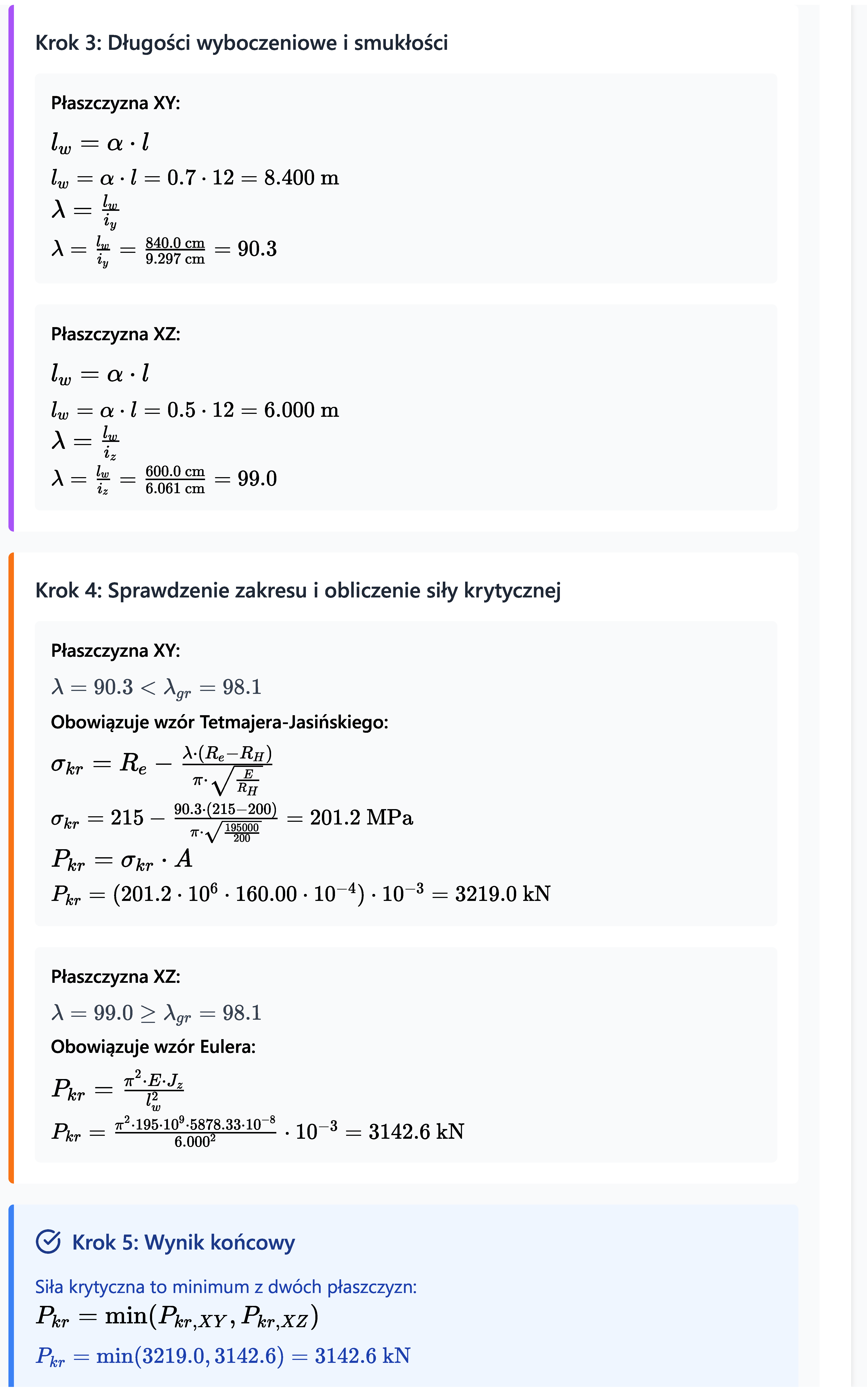
Rozwiązanie
Rozwiązanie pochodzi z kalkulatora na naszej stronie -> Kalkulator Stateczności Osiowo Ściskanych Prętów <-.