Lista zadań
Przykład 1
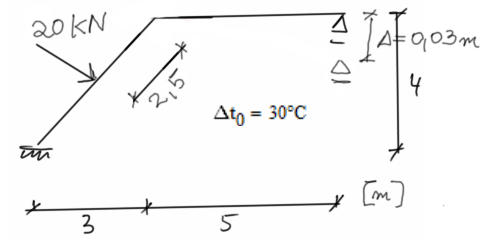
Dla przedstawionej ramy, oddzielnie dla każdego z obciążeń \(P, G, T\), wyznacz wykresy momentów zginających \(M_{\text {ost }}^P \), \(M_{\text {ost }}^G\), \(M_{o s t}^T\).
Następnie zsumuj otrzymane wykresy aby uzyskać \(M_{\text {ost }}^{P+G+T}\), na podstawie którego wyznacz \(Q_{o s t}^{P+G+T}\) oraz \(N_{o s t}^{P+G+T}\).
Dane:
\(
\alpha=10^{-5} \frac{1}{^o \mathrm{C}} \\
E J=2000 \mathrm{kNm}^2
\)
Przykład 2
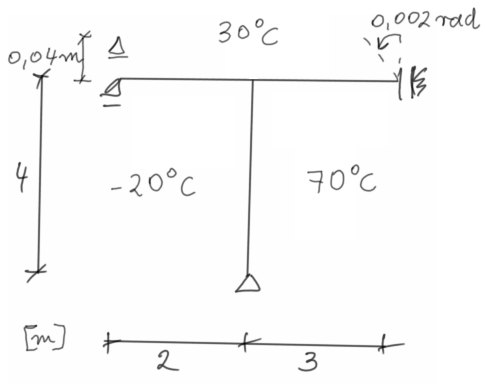
Narysować ostateczne wykresy momentów osobno od obciążeń spowodowanych przemieszczeniami podpór, termicznych od temperatury nierównomiernej i równomiernej.
Następnie zsumować otrzymane wykresy i z powstałego wykresu wyznaczyć \(Q_{o s t}^{G+T}\) oraz \(N_{o s t}^{G+T}\).
Dane:
\(
\alpha=10^{-5} \quad \text { współczynnik rozszerzalności termicznej } \\
\mathrm{EI}=2 \cdot 10^4 \mathrm{kNm}^2 \\
\mathrm{~h}:=0.2 \ m\\
\mathrm{t}_{\mathrm{m}}=10^o \mathrm{C}
\)
Przykład 4
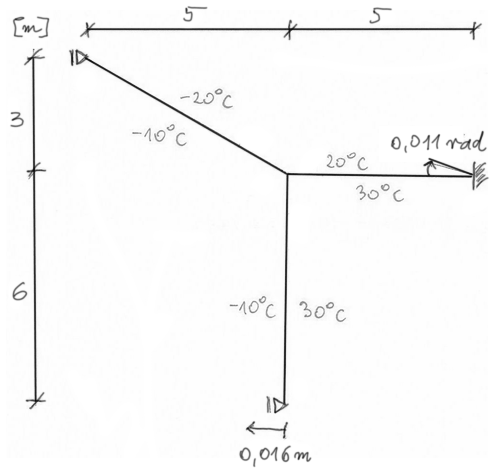
Narysować wykresy momentów gnących osobno od obciążeń spowodowanych przemieszczeniami podpór, termicznych od temperatury równomiernej i nierównomiernej.
Następnie zsumować wykresy momentów i na podstawie tego wykresu wykonać ostateczne wykresy sił tnących i normalnych.
Przyjąć przekrój prostokątny 0,2x0,8m (bxh). Założyć E=20 GPa, \( t_m=10^o C \), \( \alpha = 1\cdot 10^{-5} \ \frac{1}{^o C} \) .
Przykład 5
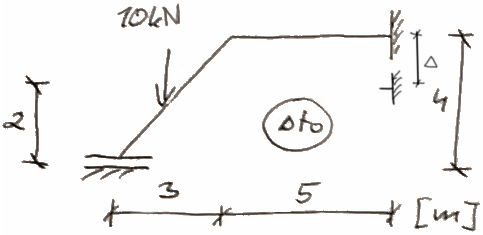
Narysować wykresy momentów gnących osobno od obciążeń spowodowanych przemieszczeniami podpór, termicznych od temperatury równomiernej i nierównomiernej.
Następnie zsumować wykresy momentów.
Przyjąć sztywność na zginanie EI=2000 \( kNm^2 \). Dane: \( \Delta = 0,03 \ m \) E=20 GPa, \( \Delta t_0 = 30^o C \), \( \alpha = 1\cdot 10^{-5} \ \frac{1}{^o C} \) .
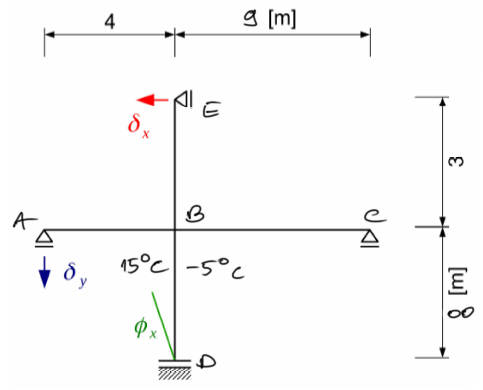
Przykład 6
Narysować wykresy momentów gnących osobno od obciążeń spowodowanych przemieszczeniami podpór, termicznych od temperatury równomiernej i nierównomiernej.
Następnie zsumować wykresy momentów i na podstawie tego wykresu wykonać ostateczne wykresy sił tnących i normalnych.
Przyjąć sztywność na zginanie EI=20 000 \( kNm^2 \). Założyć h=0,2 m, \( t_m=5^o C \), \( \alpha = 1\cdot 10^{-5} \ \frac{1}{^o C} \) .
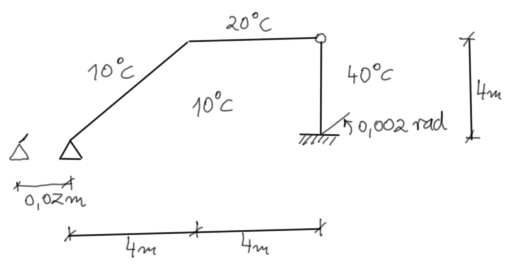
Przykład 7
Narysować wykresy momentów gnących osobno od obciążeń spowodowanych przemieszczeniami podpór, termicznych od temperatury równomiernej i nierównomiernej.
Następnie zsumować wykresy momentów i na podstawie tego wykresu wykonać ostateczne wykresy sił tnących i normalnych.
Wykonać sprawdzenie globalne.
Dane: E=205 GPa, przekrój IPE220, \( t_m=40^o C \), \( \alpha = 1,2\cdot 10^{-6} \ \frac{1}{^o C} \), \( \delta x = 6 \ cm \), \( \delta y = 4 \ cm \), \( \phi x = 0,065 rad \).
Przykład 8
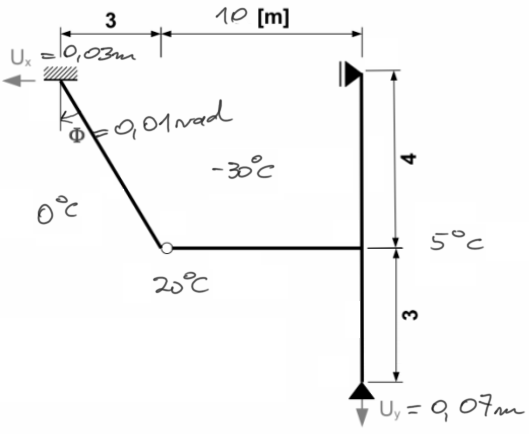
Narysować wykresy momentów gnących osobno od obciążeń spowodowanych przemieszczeniami podpór, termicznych od temperatury równomiernej i nierównomiernej.
Następnie zsumować wykresy momentów i na podstawie tego wykresu wykonać ostateczne wykresy sił tnących i normalnych.
Wykonać sprawdzenie globalne.
Dane: E=205 GPa, przekrój IPE120, \( t_m=-15^o C \), \( \alpha = 1,2\cdot 10^{-6} \ \frac{1}{^o C} \), \( U_x = 3 \ cm \), \( U_y = 7 \ cm \), \( \phi = 0,01 rad \).
