Edupanda » Mechanika techniczna » Statics - Planar force system » Equilibrium of a planar arbitrary system of forces II
List of examples
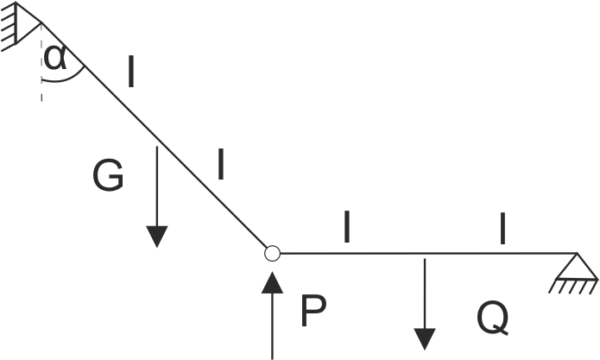
Example 1
There is a frame supported as shown in the diagram. Release the structure from constraints and write the equilibrium equations.
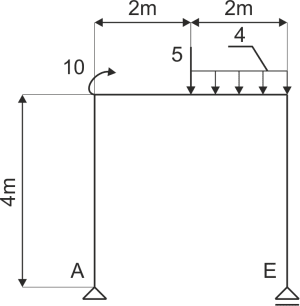
Example 2
The frame supported as shown in the figure is given. Release the system from constraints and write the equilibrium equations.
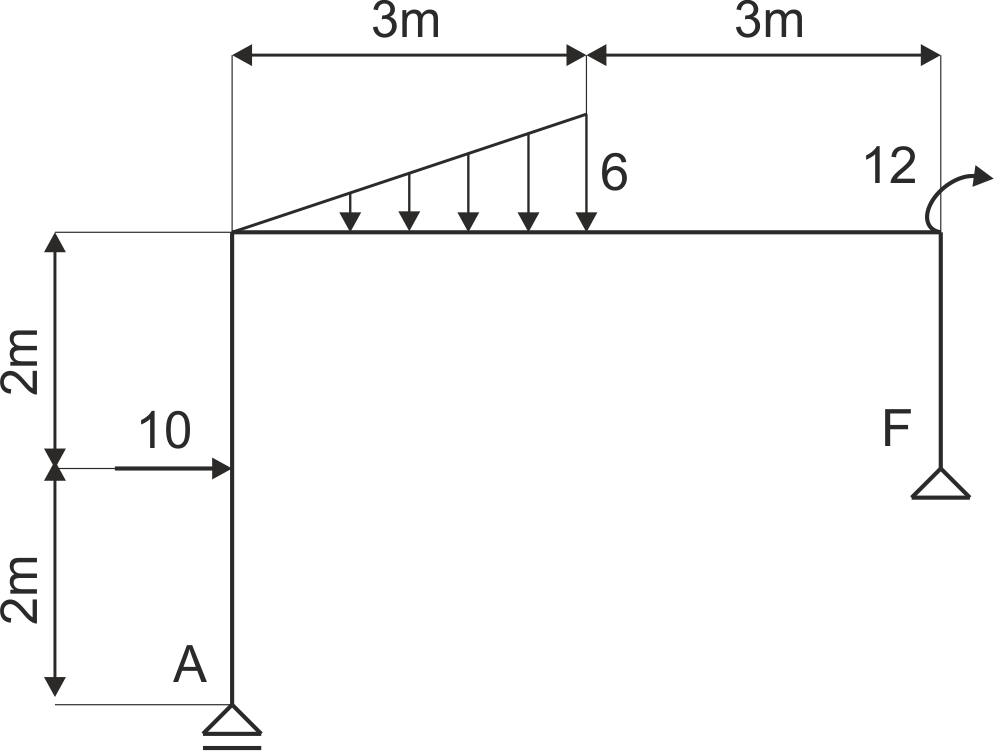
Example 3
The frame shown in the diagram is given. Release the structure from constraints and write the equilibrium equations. \( \alpha = 45^0 \).
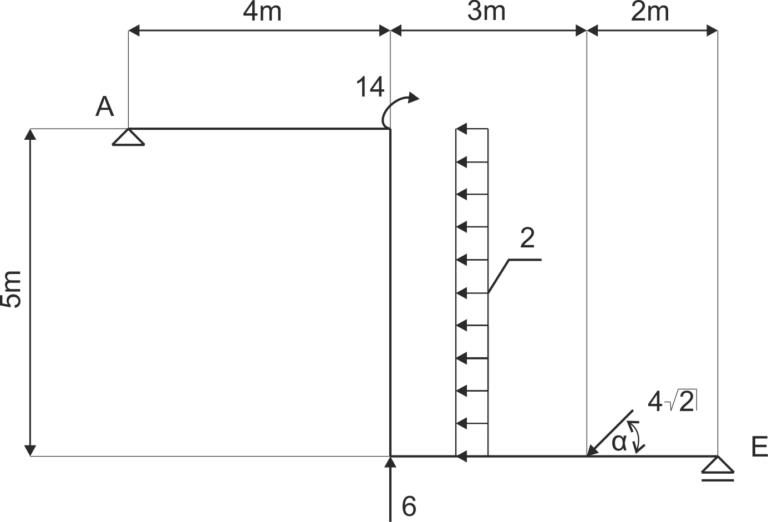
Example 4
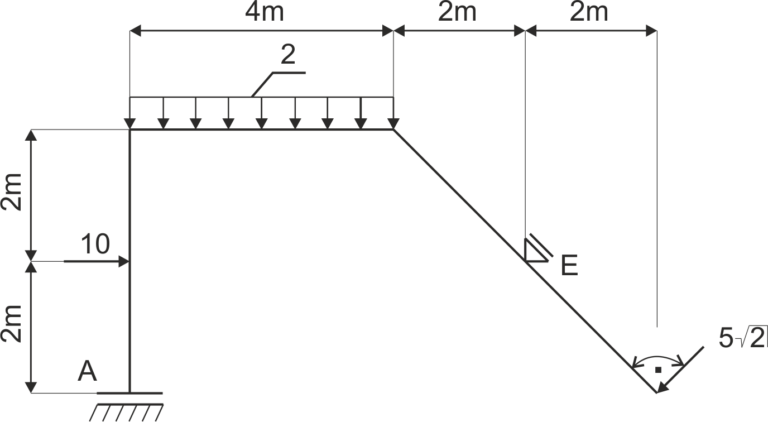
A frame supported as shown in the diagram is given. Free the system from restraints and write the equations of equilibrium.
Example 5
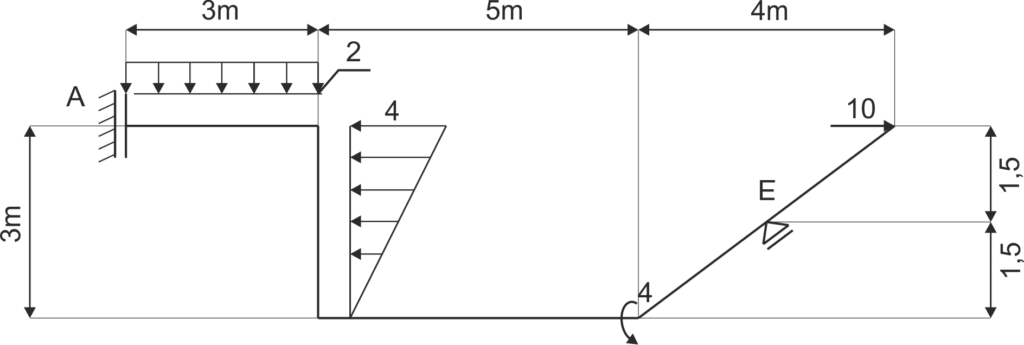
A frame supported as shown in the diagram is given. Release the system from constraints and write balance equations.
Example 6
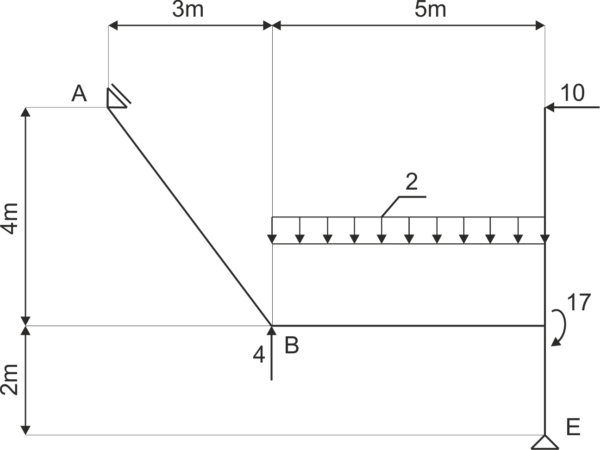
The frame shown in the diagram is given. Release the system from constraints and write the equilibrium equations.
Example 7
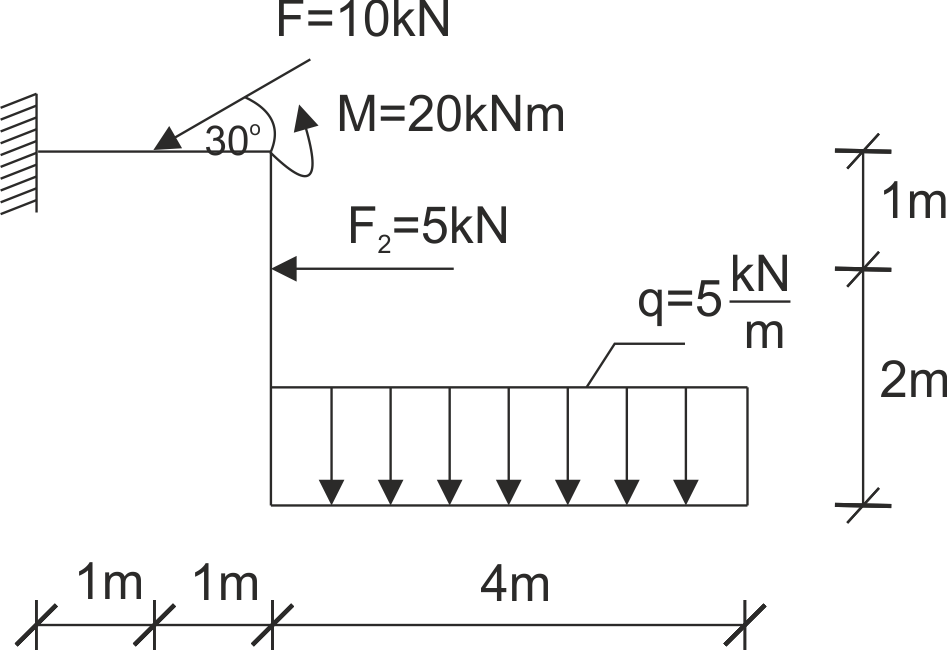
A frame supported as shown in the illustration is given. Release the structure from constraints and write the equilibrium equations.
Example 8
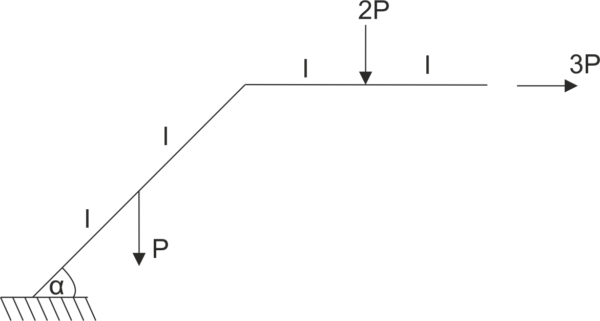
The frame is supported as shown in the diagram. Release the system from constraints and write the equations of equilibrium.
Example 9
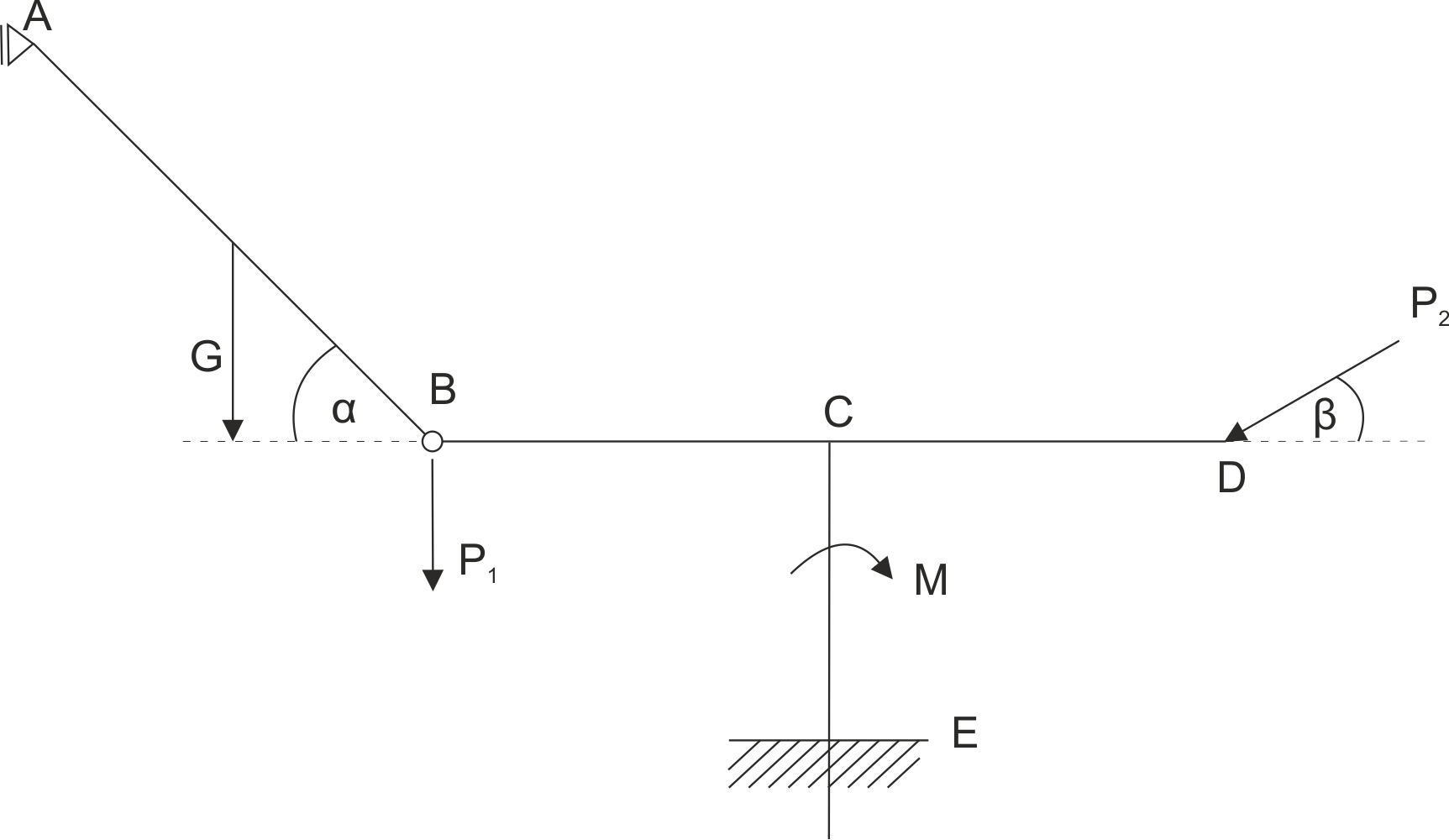
Calculate the support reactions and reactions at the hinge. Data: AB=2a, BC=CD=a, CE=b.
Example 13
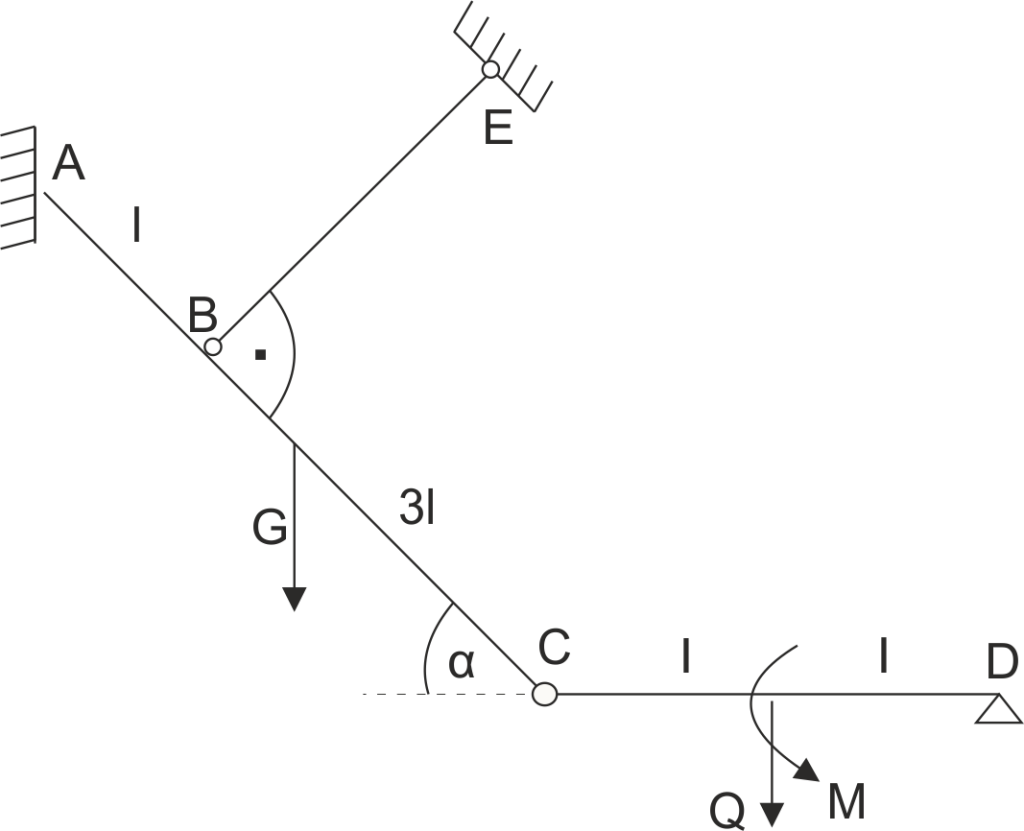
A beam-and-rod system is given. Beam AC (with weight G) and beam CD (with weight Q) are articulatedly connected. Beam AC is freely supported at point A, additionally suspended by the cable BE. Calculate support reactions and reactions at the joint.
Example 14
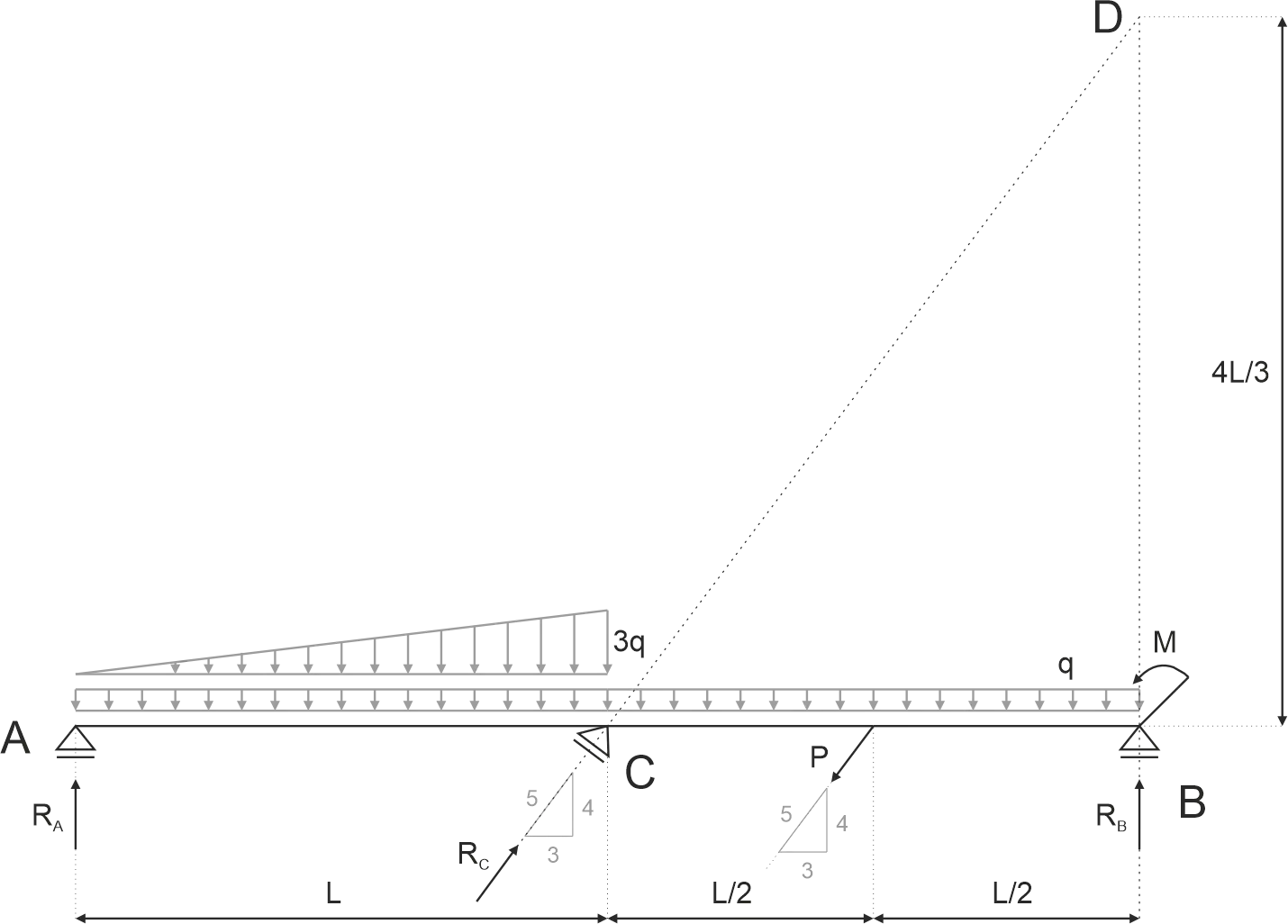
Determine the values of reactions \(R_A\), \(R_B\), and \(R_C\) in the beam shown in the figure. Assume a moment \(M = 400 kNm\), a force \(P = 100 kN\), a distributed load \(q = 10 kN/m\), and a length \(L = 10 m\).