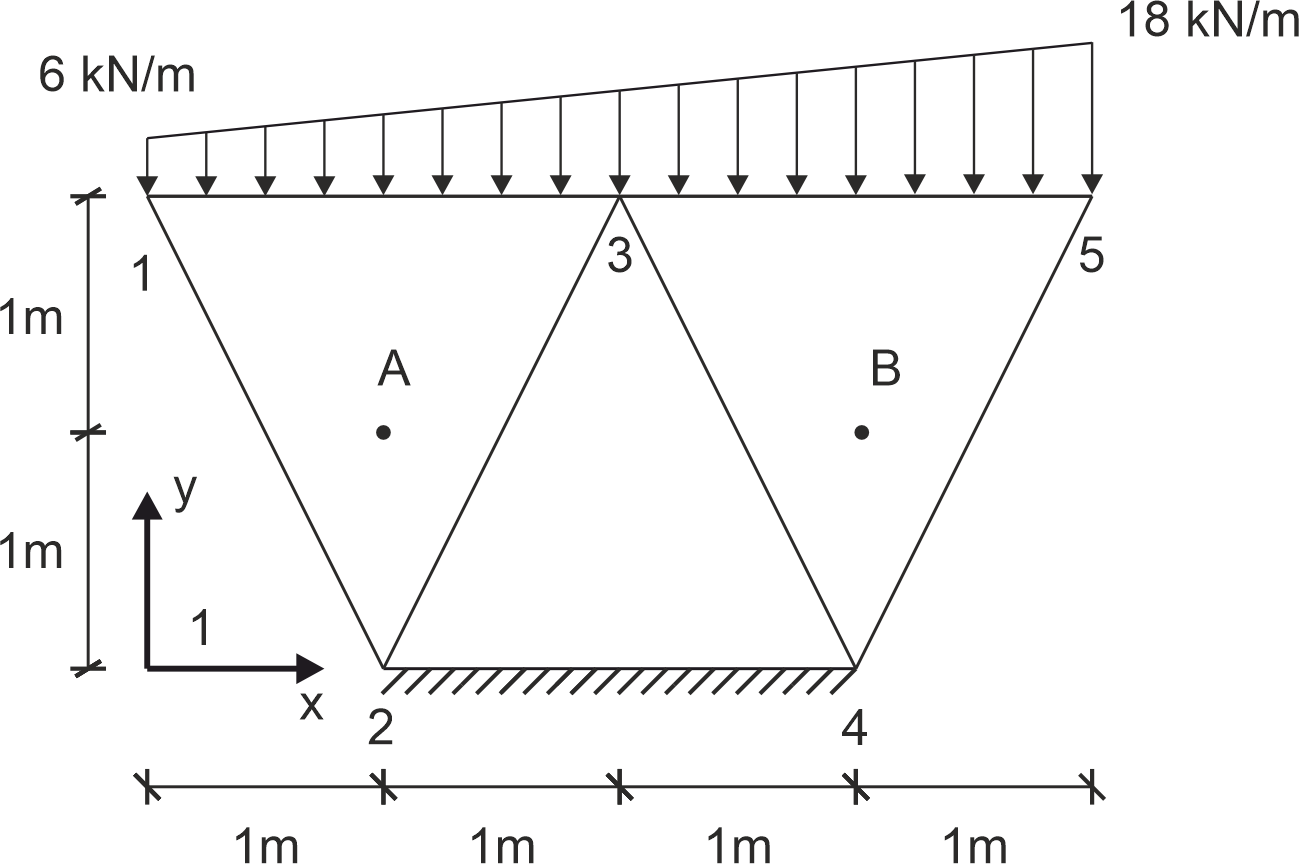
Dla podanego układu w PSO zdyskretyzowanego elementami skończonymi jak na rysunku wyznaczyć globalny wektor prawej strony równania MES oraz wyznaczyć:

1 wektor przemieszczeń \(u\)

2 wszystkie z definicji niezerowe składowe wektorów odkształcenia e i naprężenia s

w punkcie \(A\) oraz \(B\).

\[ E = 27 \, \text{GPa}, \quad \nu = 0.2 \] \[ \mathbf{d} = \begin{bmatrix} 1.90 \\ -8.86 \\ 0 \\ 0 \\ 4.74 \\ -8.73 \\ 0 \\ 0 \\ 10.4 \\ -24.5 \end{bmatrix} \cdot 10^{-7} \, \text{m} \]