1. Determination of the degree of kinematic indeterminacy:

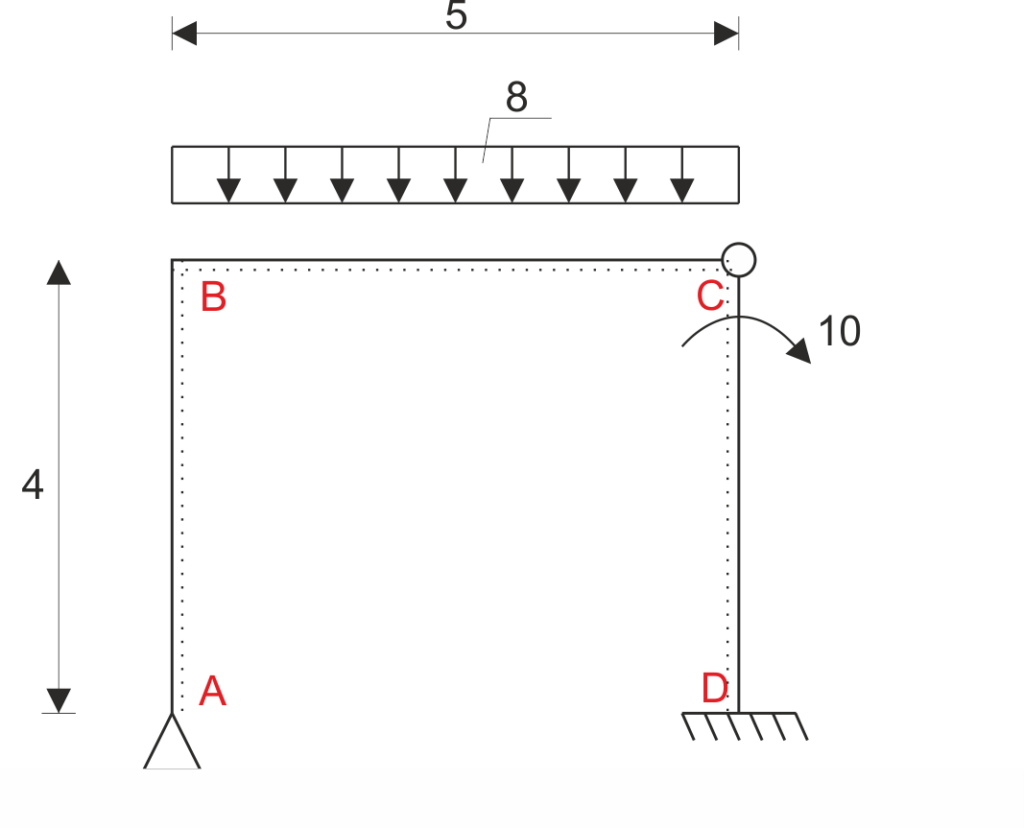
\[\begin{aligned} &SKN=\sum \varphi +\sum \Delta\\ &SKN=1+1=2\\ \end{aligned}\]

2. Selection of the basic system of displacement method (UPMP):

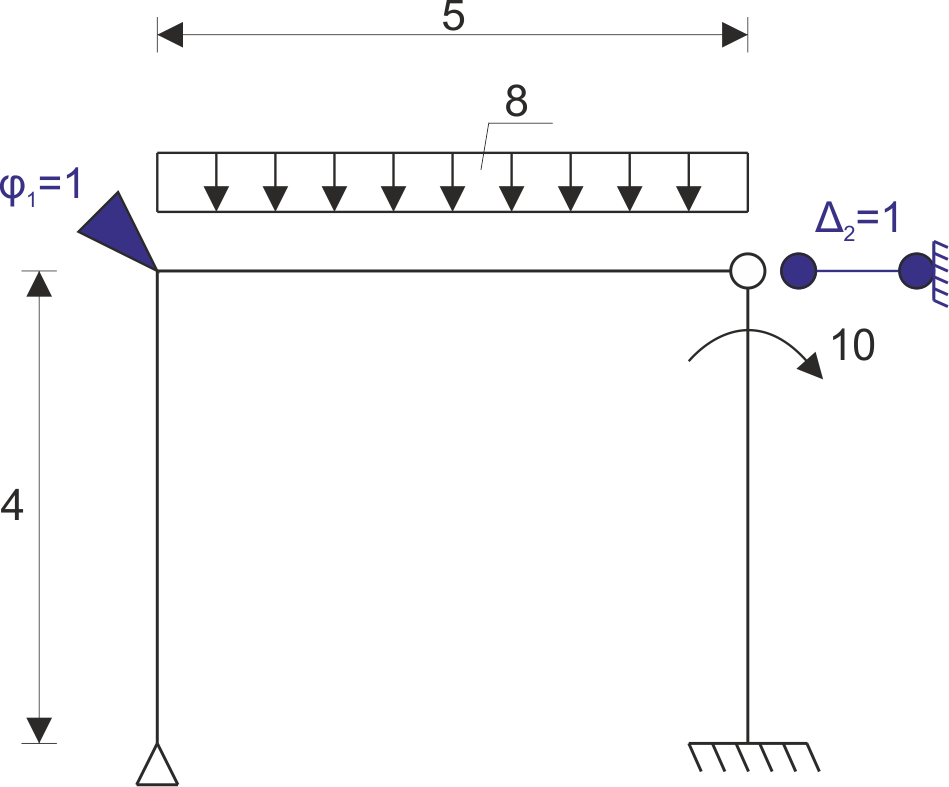
Canonical equation system of the displacement method:
\[ r_{11}\cdot\varphi_{1} +r_{12}\cdot\Delta_{2}+r_{1p}=0\\ r_{21}\cdot\varphi_{1} +r_{22}\cdot\Delta_{2}+r_{2p}=0\\ \]

3. Graphs and determination of coefficients and constants of the equation:

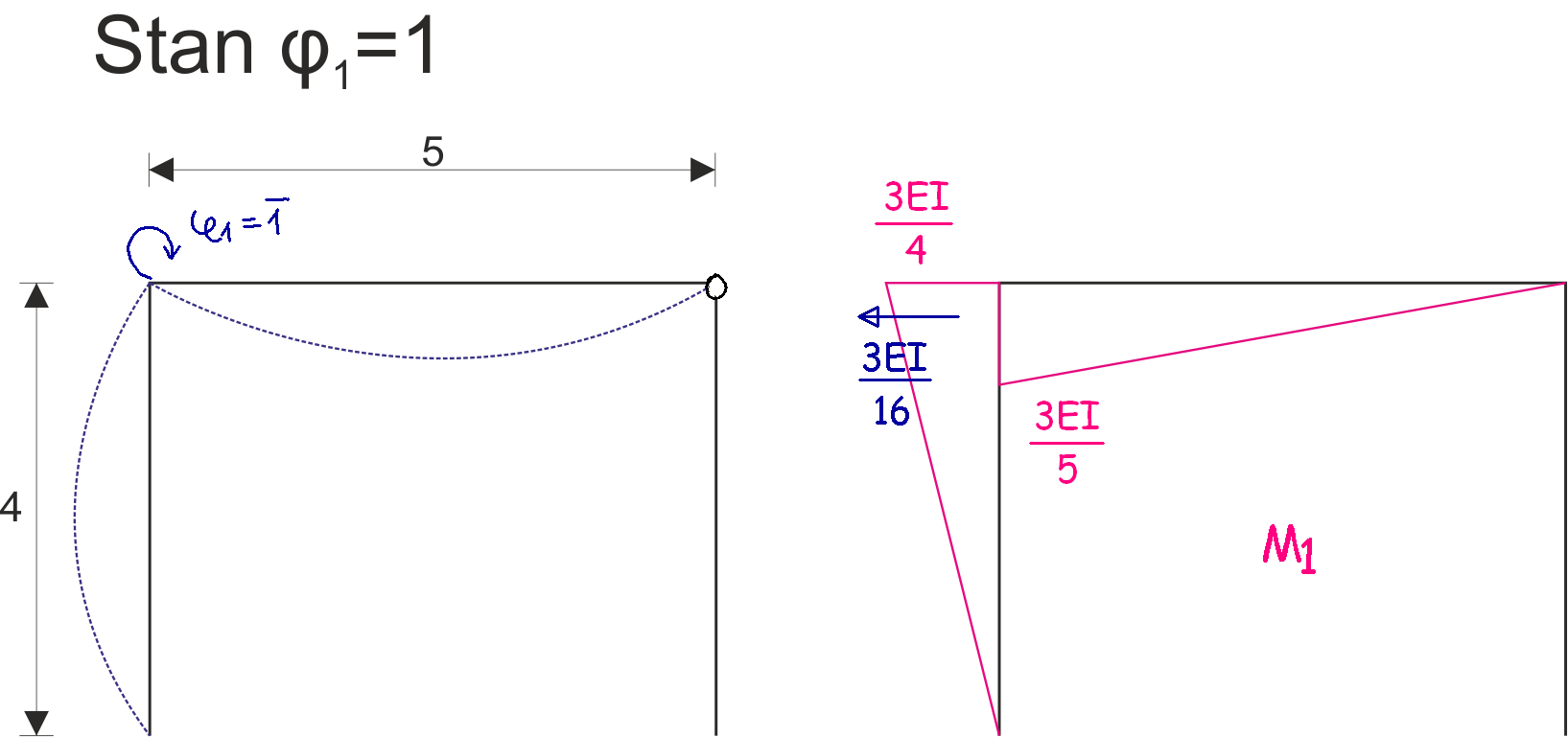
Determination of UPMP coefficients

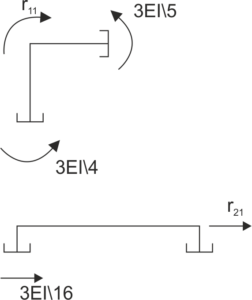
\[\begin{aligned} &r_{11}=\frac{3EI}{5}+\frac{3EI}{4}=\frac{27EI}{20}\\ \\ \\ &r_{21}=-\frac{3EI}{16}\\ \end{aligned}\]

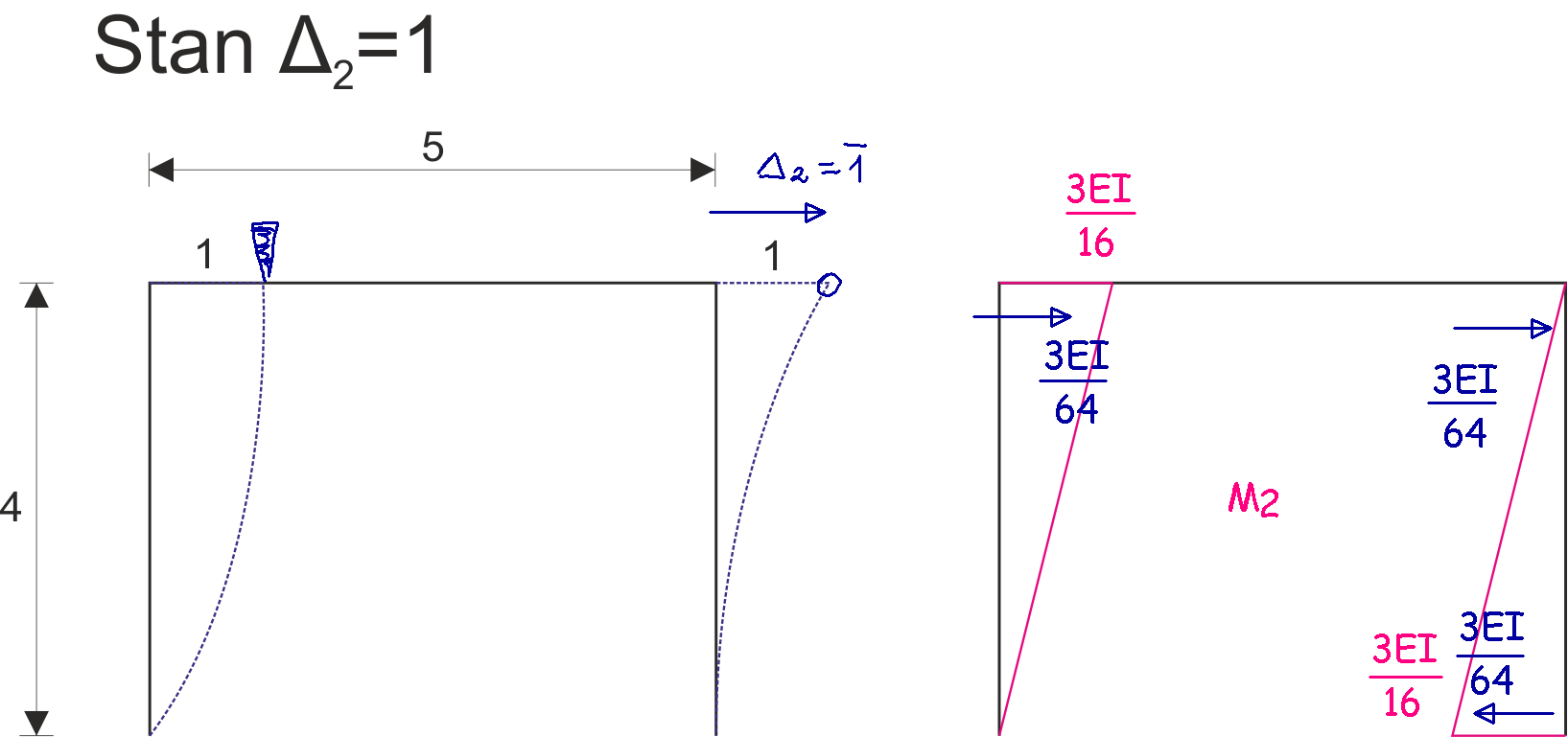
Determination of UPMP coefficients

\[\begin{aligned} &r_{12}=-\frac{3EI}{16}\\ \\ \\ &r_{22}=\frac{3EI}{32}\\ \end{aligned}\]

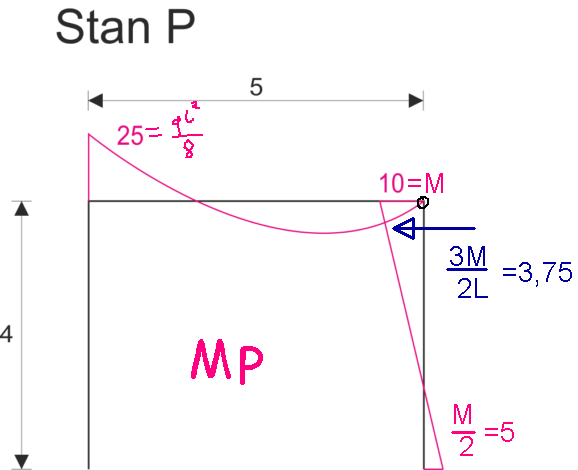
Determination of UPMP coefficients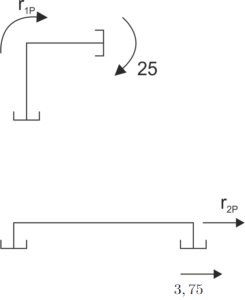

\[\begin{aligned} &r_{1p}=-25\\ \\ \\ \\ &r_{2p}=-3,75\\ \end{aligned}\]

4. Solution of the canonical equation system:

\[\begin{aligned} &\frac{27EI}{20}\cdot\varphi_{1} -\frac{3EI}{16}\cdot\Delta_{2}=25\\ &-\frac{3EI}{16}\cdot\varphi_{1} +\frac{3EI}{32}\cdot\Delta_{2}=3,75\\ \\ &\varphi_{1} =33,33/EI\\ &\Delta_{2}=106,67/EI\\ \end{aligned}\]

5. Final diagrams of internal forces in the frame:

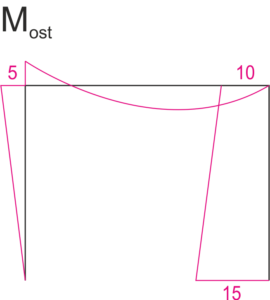
Moment diagram [kNm]
\[ M_{ost}=M_{p}+M_{1} \cdot \varphi_{1}+M_{2} \cdot \Delta_{2}\\ \]

\[\begin{aligned} & \mathrm{M}_{\mathrm{A}}=0 \cdot \mathrm{kNm} \\ & \mathrm{M}_{\mathrm{BA}}=\frac{-3 \mathrm{EI}}{4} \cdot \varphi_1+\frac{3 \mathrm{EI}}{16} \cdot \Delta_2=-5 \mathrm{kNm} \\ & \mathrm{M}_{\mathrm{BC}}=\frac{3 \mathrm{EI}}{5} \varphi_1-25=-5 \mathrm{kNm} \\ & \mathrm{M}_{\mathrm{CB}}=0 \cdot \mathrm{kNm} \\ & \mathrm{M}_{\mathrm{CD}}=10 \cdot \mathrm{kNm} \\ & \mathrm{M}_{\mathrm{D}}=\frac{3 \mathrm{EI}}{16} \cdot \Delta_2-5=15 \mathrm{kNm} \end{aligned}\]

Calculations for the shear force diagram

Element BC: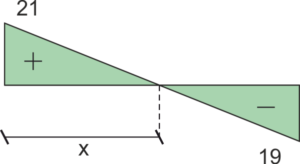

\[\begin{aligned} &\sum{M_{C}}=0\\ &{Q_{BC}}\cdot 5-5-8\cdot 5\cdot 2,5=0\\ &{Q_{BC}}=21 \ kN\\ &\sum{Y}=0\\ &-{Q_{CB}}+21-40=0\\ &{Q_{CB}}=-19 \ kN\\ \end{aligned}\] Coordinates of the extreme value of the moment in element BC: \[\begin{aligned} &\frac{x}{21}=\frac{5-x}{19}\\ &x=2,625 \ m\\ \end{aligned}\] Extreme moment value \[ \mathrm{M}_{\mathrm{ex}}=-5-8 \cdot 2.625 \cdot \frac{2.625}{2}+21 \cdot 2.625=22.56 \mathrm{kNm} \]

Element AB: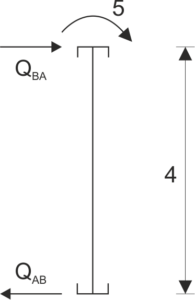

\[\begin{aligned} &\sum{M_{A}}=0\\ &{Q_{BA}}\cdot 4+5=0\\ &{Q_{BA}}=-1,25 \ kN\\ &{Q_{AB}}=-1,25\\ \end{aligned}\]

Element CD:

\[\begin{aligned} &\sum{M_{D}}=0\\ &{Q_{CD}}\cdot 4+10-15=0\\ &{Q_{CD}}=1,25 \ kN\\ &{Q_{DC}}=1,25 \ kN\\ \end{aligned}\]

Final diagram of axial forces [kN]

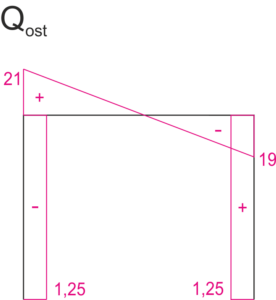
6. Kinematic verification

We assume a determinable system and draw a graph of moments from the unit force. (degree of static indeterminacy DSI = 1)

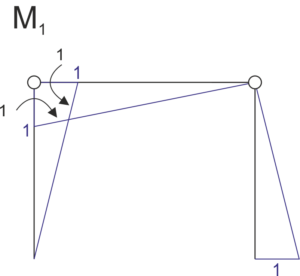\[\begin{aligned} &\delta_1 =\int \frac{M_{ost}\cdot M_{1}}{EJ} dx= \frac{1}{EI} \left( -\frac{1}{3}\cdot 1\cdot 5\cdot 4 -\frac{1}{3} \cdot 1\cdot 5\cdot 5 +\frac{1}{3} \frac{8\cdot 5^2}{8} \cdot 1 \cdot 5 -\frac{4}{6} \cdot (2\cdot 1\cdot 15 + 10)\right) \approx 0\\ \end{aligned}\]

7. Static verification

We read the reactions (values and correct directions) from the diagrams of normal forces, shear forces, and bending moments.
Then we write down the equations of static equilibrium and check if all equations are satisfied for the read reactions.

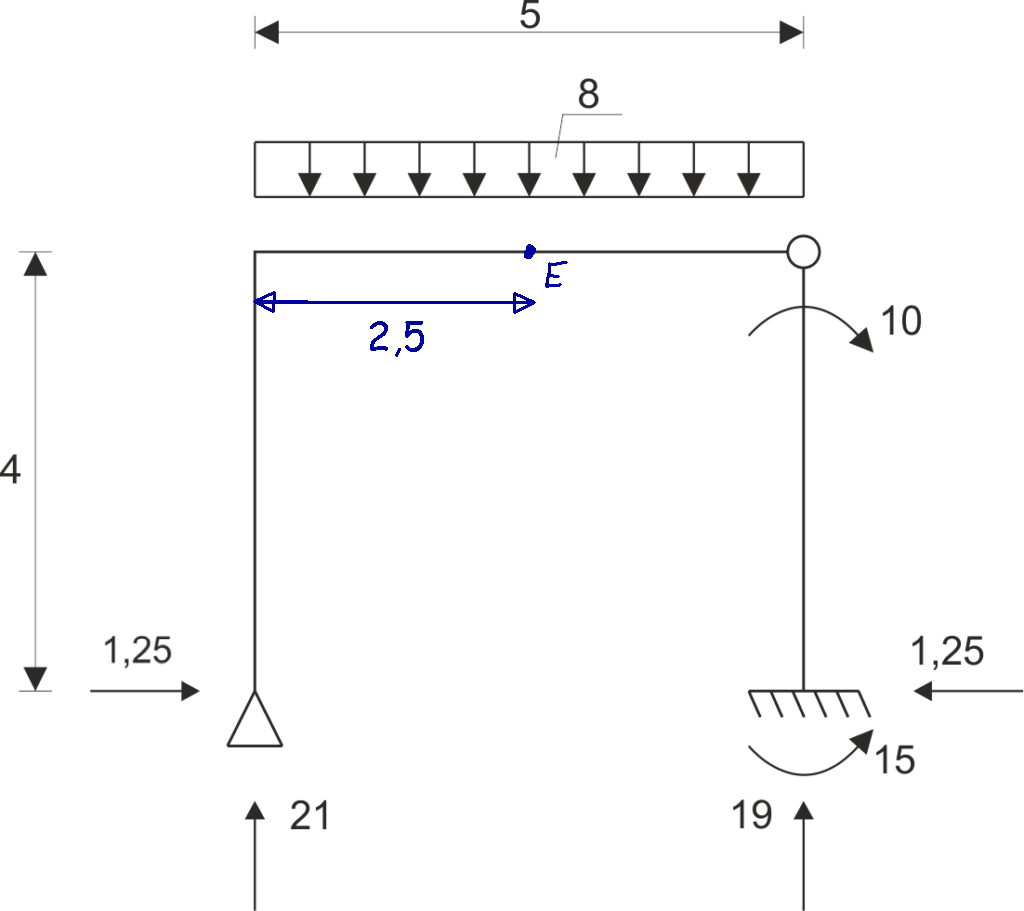
\[\begin{aligned} &\sum{X}=0 \hspace{2cm} 1,25-1,25=0\\ &\sum{Y}=0 \hspace{2cm} 21+19-4\cdot8=0\\ &\sum{M_{E}}=0\hspace{1.65cm} 21\cdot 2,5-1,25\cdot 4+10-15+1,25\cdot 4-19\cdot 2,5=0\\ \end{aligned}\]