Edupanda » Strength of materials » Axial Tension and Compression » Statically Determinate - Bar Systems
List of examples
Example 1
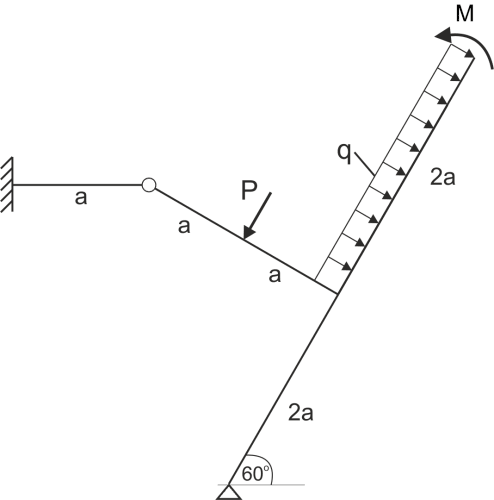
Calculate the diameter of the rod d and the elongation of the rod \(\Delta_l\).
Data: \(a=1 m, P=15 kN, q=8 \frac{kN}{m}, M=6 kNm, k_r=80 MPa, k_c=120 MPa, E=2\cdot10^5 MPa\)
Example 2

Calculate the distance x at which the concentrated force P should be applied in order to cause parallel movements of the beam AB downwards. All bars have the same circular cross-section.
Data: \(l=1 m, P=10 kN\)
Example 3

On the ABC support composed of a copper support AB and a steel tie rod AC, a weight G = 50 kN is suspended. Determine the diameter D of the tie rod and the dimension a of the square cross-section of the copper support AB, assuming the permissible stresses for copper and steel. Determine the horizontal and vertical displacement of point A.
Data: \( k_c (m) = 40 MPa, k_r (st) = 160 MPa, E_s = 2.1 \cdot 10^5 MPa, E_m = 1.15 \cdot 10^5 MPa, AB = 1.2 m\)
Example 6

Calculate the diameter of the rod d and the vertical displacement of point C. The OC element is a rigid beam, and the AB element is a tie (lattice rod).
Data: \(k_r=k_c=100 MPa, E=200 GPa\)
Example 7

Calculate the diameter of the rod d and the elongation of the rod \(\Delta_l\).
Data: \( k_r=k_c=100 MPa, E=2\cdot 10^5 MPa\)
Example 8

Calculate the diameter of the rod d and the elongation of the rod \(\Delta_l\).
Data: \(k_r=k_c=100 MPa, E=2\cdot 10^5 MPa\)
Example 9

Calculate the diameter of the rod d and the elongation of the rod \(\Delta_l\).
Data: \(a=1 m, P=10 kN, q=6 kN/m, M=8 kNm, k_r=80 MPa, k_c=120 MPa, E=2\cdot10^5 MPa\)
Example 10

Calculate the diameter of the rod d and the elongation of the rod \(\Delta_l\).
Data: \(k_r=k_c=100 MPa, E=2\cdot 10^5 MPa\)
Example 11
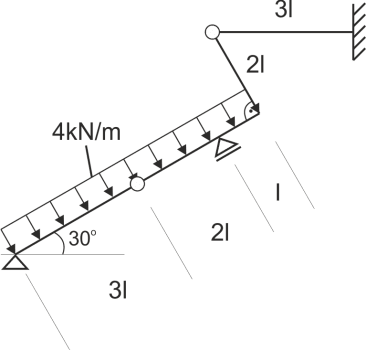
Calculate the diameter of the rod d and the elongation of the rod \(\Delta_l\).
Data: \(l=1 m, k_r=k_c=120 MPa, E=200 GPa\)
Example 12

Calculate the diameter of the rod d and the elongation of the rod \(\Delta_l\).
Given: \(k_r=80 MPa, k_c=60 MPa, E=200 GPa\)
Example 15

Calculate the diameter of the rod d and the vertical displacement of point C.
Given: kr=120 MPa, E=210 GPa
Example 16

Calculate the diameter of the rod d, elongation of the rods \(\Delta_l\), and displacement of point B.
Data: \(P=30 kN, k_{g_{BC}}=60 MPa, k_{g_{AB}}=180 MPa, E_{BA}=210 GPa, E_{BC}=10 GPa\)




