Equivalent resistance

Sometimes, before we start calculating a task related to an electrical circuit, we can simplify it by replacing several resistors (or other elements, e.g. in the case of analyzing AC circuits using symbolic methods) with one that represents the equivalent resistance (in the case of analyzing AC circuits, impedance).

There are several tasks in which calculating the equivalent resistance is necessary for other reasons - compare, for example, the Thevenin's method or Norton's method.

Series connection

If the elements are connected in series:

1. The current flowing through them has the same value
2. The equivalent resistance is the sum of the resistances of the individual elements
\begin{aligned} &R_{eq}=R_1+R_2+...\\ &R_{eq}=\sum{R_i} \end{aligned}

It is very important to notice that determining whether the elements are connected in series depends on whether the same current flows through them, which will be more visible in the examples.

Parallel connection

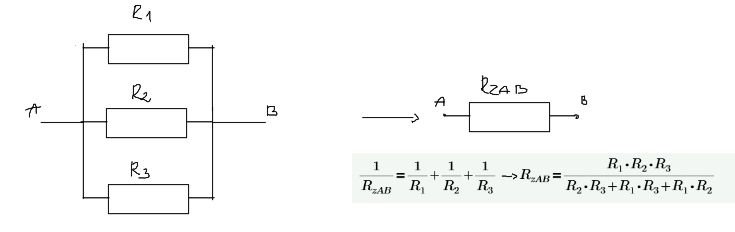
If the elements are connected in parallel:

1. The voltage across them has the same value
2. The equivalent conductance is the sum of the conductances of the individual elements
\begin{aligned} &G_{eq}=G_1+G_2+...\\ &G_{eq}=\sum{G_i} \end{aligned}
3. The reciprocal of the equivalent resistance is the sum of the reciprocals of the resistances of the individual elements
\begin{aligned} &\frac{1}{R_{eq}}=\frac{1}{R_1}+\frac{1}{R_2}+...\\ &\frac{1}{R_{eq}}=\sum{\frac{1}{R_i}}\\ \end{aligned}

It is very important to notice that determining whether the elements are connected in parallel depends on whether the same voltage occurs across them.

For clarity - using the conductance formula is rarely actually beneficial, but it helps to see the relationship that occurs for this type of element connection.

In practice, it is also worth remembering the formula for two elements connected in parallel:

\begin{aligned} &\frac{1}{R_{eq}}=\frac{1}{R_1}+\frac{1}{R_2}=\frac{R_2}{R_1\cdot R_1 }+\frac{R_1}{R_2\cdot R_1 }\\ &\frac{1}{R_{eq}}=\frac{R_1+R_2}{R_1\cdot R_2}\\ &R_{eq}=\frac{R_1\cdot R_2}{R_1+R_2}\\ \end{aligned}

If you ever have doubts about what is in the denominator and what is in the numerator, remember that in the end the correct unit - \(\Omega\), must come out, so multiplication MUST be in the numerator because:

\begin{aligned} &\frac{\Omega\cdot \Omega}{\Omega + \Omega}=\frac{\Omega^2}{\Omega}=\Omega\\ \end{aligned}

and not:

\begin{aligned} &\frac{\Omega+\Omega}{\Omega \cdot \Omega}=\frac{\Omega}{\Omega^2}=\frac{1}{\Omega}\\ \end{aligned}

Mixed connection (series - parallel)

Personally, I don't like this term very much :-) In practice, a mixed connection still needs to be reduced to a superposition of series and parallel connections, so I don't see any particular reason to consider it as a separate case.

However, at this point, I will allow myself a little digression - every equivalent resistance is calculated with respect to two points (terminals), it is not an absolute value but only a simplification that we use to make our lives easier.

Equivalent resistance with Kirchhoff's laws

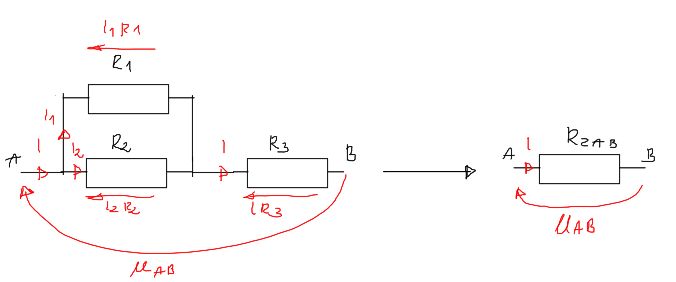
A VERY useful approach to thinking about equivalent resistance, especially in more complex and non-obvious cases that sometimes appear, for example, in tasks with Thevenin's method, is the approach to it from the Kirchhoff's laws perspective.

Let's imagine for a moment that there is a voltage \(U_{AB}\) between terminals AB, with respect to which we are to calculate the equivalent resistance, causing a current \(I\) to flow.

It is obvious that \(R_{eq}=\frac{U_{AB}}{I}\)

Given:

\begin{aligned} R_1 & =30 \\ R_2 & =20 \\ R_3 & =10 \end{aligned}

Using the formulas for series and parallel connection:

\begin{aligned} &R_{12}=\frac{R_1 \cdot R_2}{R_1+R_2}=12\\ &R_{eq AB}=R_{12}+R_3=22 \end{aligned}

Using Kirchhoff's laws:

\begin{aligned} & I=I_1+I_2 \\ & I_1 \cdot R_1=I_2 \cdot R_2 \\ & U_{A B}=I_2 \cdot R_2+I \cdot R_3 \\ & R_{eq A B}=\frac{U_{A B}}{I} \end{aligned}

Calculating:

\begin{aligned} & I_1=\frac{I_2 \cdot R_2}{R_1} \\ & I=\frac{I_2 \cdot R_2}{R_1}+I_2 \\ & I_2=\frac{R_1 \cdot I}{R_2+R_1} \\ & U_{A B}=\frac{R_1 \cdot I}{R_2+R_1} \cdot R_2+I \cdot R_3 \\ & R_{eq A B}=\frac{\frac{R_1 \cdot I}{R_2+R_1} \cdot R_2+I \cdot R_3}{I}=\frac{R_1}{R_2+R_1} \cdot R_2+R_3=22 \end{aligned}

And of course, this is not actually calculating the equivalent resistance, but in more complex cases, this way of thinking can be very helpful, although the calculations themselves will generally be more complicated.

Example 1

Given:

\begin{aligned} & R_1=10 \\ & R_2=20 \\ & R_3=10 \\ & R_4=10 \\ & R_5=20 \end{aligned}
\begin{aligned} &R_{12}=R_1+R_2=30\\ \end{aligned} \begin{aligned} &R_{45}=R_4+R_5=30\\ \end{aligned} \begin{aligned} &R_{345}=\frac{R_3 \cdot R_{45}}{R_3+R_{45}}=7.5\\ \end{aligned} \begin{aligned} &R_{eq}=R_{12}+R_{345}=37.5 \end{aligned}

Example 2

Given:

\begin{aligned} & R_1=10 \\ & R_2=20 \\ & R_3=10 \\ & R_4=10 \\ & R_5=20 \end{aligned} \begin{aligned} & I=I_1+I_2 \\ & I_1+I_2=I_3+I_4 \\ & I_1 \cdot R_1-I_2 \cdot R_2=0 \\ & -I_3 \cdot R_3+I_4 \cdot R_4+I_4 \cdot R_5=0 \\ & -U_{AB}+I_3 \cdot R_3+I_1 \cdot R_1=0 \\ & R_{eq AB}=\frac{U_{AB}}{I} \end{aligned} \begin{array}{ll} -U_{AB}+I_3 \cdot R_3+I_1 \cdot R_1=0 & U_{AB}=10 \cdot I_3+10 \cdot I_1 \\ -I_3 \cdot R_3+I_4 \cdot R_4+I_4 \cdot R_5=0 & I_4=\frac{I_3}{3} \\ I_1 \cdot R_1-I_2 \cdot R_2=0 & I_2=\frac{I_1}{2} \\ I=I_1+I_2 & I_1=I-I_2=\frac{2 \cdot I}{3} \\ I-\frac{I_1}{2}+\frac{I_1}{2}=I_3+\frac{I_3}{3} & I_3=\frac{3 \cdot I}{4} \end{array} \begin{aligned} &U_{AB}=10 \cdot \frac{3 \cdot I}{4}+10 \cdot \frac{2 \cdot I}{3}=\frac{85 \cdot I}{6}\\ &R_{eq AB}=\frac{U_{AB}}{I}=\frac{85}{6}=14.167 \end{aligned}

For comparison, using the formulas for the equivalent resistance:

\begin{aligned} &R_{12}=\frac{R_1 \cdot R_2}{R_1+R_2}=6.667\\ & R_{45}=R_4+R_5=30 \\ & R_{345}=\frac{R_3 \cdot R_{45}}{R_3+R_{45}}=7.5 \\ & R_{eq AB}=R_{12}+R_{345}=14.167 \end{aligned}