Metoda Thevenina

Twierdzenie Thevenina, nazywane również twierdzeniem o zastępczym źródle napięcia, brzmi na początku dość skomplikowanie, ale jego użycie okaże się bardzo proste, kiedy zobaczymy je na przykładzie.
Nie będziemy wchodzić zbyt głęboko w teorię stojącą za tym twierdzeniem, w sporym uproszczeniu mówo ono, że:
Stacjonarny, liniowy i skupiony obwód elektryczny można zastąpić obwodem złożonym z idealnego źródła napięcia (źródło Thevenina) oraz impedancji (rezystora w obwodach prądu stałego).
Co istotne metoda ta służy co obliczania prądu w pojedynczej gałęzi układu więc jest świetna do weryfikacji obliczeń dokonanych inny metodami, ułatwia też wiele bardziej zaawansowanych zagadnień.
Kroki metody:
- Wyłączamy z obwodu gałąź dla której prąd chcemy policzyć
- Dla reszty obwodu obliczamy:
- Napięcie źródła Thevenina
- Impedancję (rezystancję) zastępczą (porównaj -> rezystancja zastępcza)
- Dołączamy te elementy do badanej gałęzi i obliczamy prąd w tej gałęzi
Przykład 1
Treść
Korzystając z metody Thevenina wyznacz prąd \(I_x\)

Dane: \(R_1=10 \Omega, R_2=20 \Omega, R_3=30 \Omega, R_4=20 \Omega, E_1=130 V, E_2=120 V\)
Rozwiązanie
Krok 1 - Wyłączamy z obwodu gałąź dla której prąd chcemy policzyć
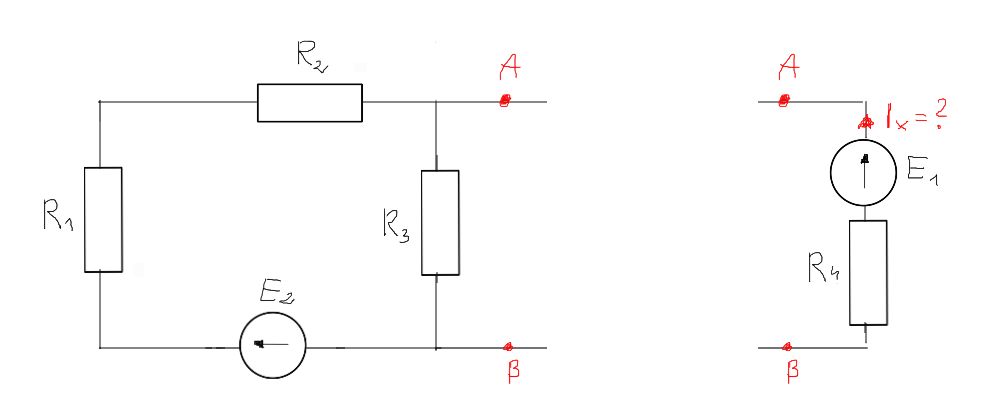
Krok 2 - Dla reszty obwodu obliczamy napięcie źródła Thevenina
 $$
\begin{aligned}
&I=\frac{E_2}{R_1+R_2+R_3}=2A\\
&E_T=-I \cdot R_3=-60V
\end{aligned}
$$
$$
\begin{aligned}
&I=\frac{E_2}{R_1+R_2+R_3}=2A\\
&E_T=-I \cdot R_3=-60V
\end{aligned}
$$
Krok 3 - Dla reszty obwodu obliczamy impedancję (rezystancję) zastępczą
 $$R_T=\frac{\left(R_1+R_2\right) \cdot R_3}{R_1+R_2+R_3}=15\Omega$$
$$R_T=\frac{\left(R_1+R_2\right) \cdot R_3}{R_1+R_2+R_3}=15\Omega$$
Krok 4 - dołączamy te elementy do badanej gałęzi i obliczamy prąd w tej gałęzi
 $$I_x=\frac{E_1+E_T}{R_T+R_4}=2A$$
$$I_x=\frac{E_1+E_T}{R_T+R_4}=2A$$

