Maxwell-Mohr Method

In this text you will learn what the Maxwell-Mohr Method is and how it works. You will see the algorithm for solving problems using this method. You will find examples of solutions.

Maxwell-Mohr Method - Simplified Approach (Consideration of Bending Moment Only)

According to the Maxwell-Mohr method, the calculation of displacement u comes down to calculating an integral, under which the bending moment caused by the actual external load (Mg) and the bending moment that would be caused by a unitary fictitious force P=1 corresponding to the sought displacement (\(M_1\)) occur.
\[ u=\int_{0}^{l} \frac{M_{g} \cdot M_{1}}{E I} d x \] In the following problems, we neglect the influence of shear forces (except for one exception) and normal forces (negligible), as well as temperature, support settlement loads, and elastic supports.

Integration can be done analytically or graphically

Example 1

Task

Calculate the vertical displacement of point D.
Take into account the influence of bending moments and shear forces.

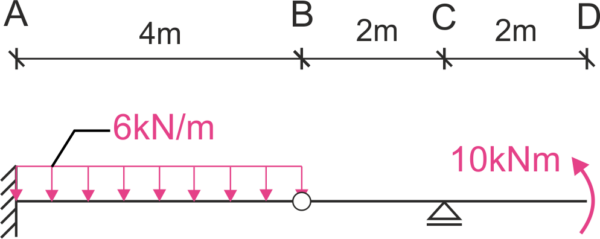
Solution

We divide the hinged beam into simple beams, calculate the reactions at the supports, and draw the internal force diagrams. Note - the reactions can be calculated without dividing into simple beams. Finding the extreme values is not necessary for calculating the displacement.

\[ \mathbb{I} \\ \sum M_{B}=0 & 10+2 V_{C}=0 \\ & V_{C}=-5 \text{kN} \\ \sum Y=0 & V_{B}+V_{C}=0 \\ & V_{B}=5 \text{kN} \] \[ \frac{29}{x}=\frac{29+5}{4}=>x=\frac{29 \cdot 4}{29+5}=\frac{58}{17} \approx 3.412 \] \[ \sum M_{A}=0 & -M_{A}-6 \cdot 4 \cdot 2-4 V_{B}=0 \\ & M_{A}=-68 \text{kNm} \\ \sum Y=0 & V_{A}-6 \cdot 4-V_{B}=0 \\ & V_{A}=29 \text{kN} \]

\[ \mathbb{I} \\ \sum M_{B}=0 & -1 \cdot 4+2 V_{C}=0 \\ & V_{C}=2 \text{kN} \\ \sum Y=0 & V_{B}+V_{C}-1=0 \\ & V_{B}=-1 \text{kN} \] \[ \sum M_{A}=0 & -M_{A}-4 V_{B}=0 \\ & M_{A}=4 \text{kNm} \\ \sum Y=0 & V_{A}-V_{B}=0 \\ & V_{A}=1 \text{kN} \] We calculate the displacement taking into account the influence of the bending moment (dominant) and the shear force. If we do not have numerical data, we leave the result in the form given below.
\[ \Delta_{D}=& \int \frac{M_{P} M_{1}}{E I} d x+\kappa \int \frac{Q_{P} Q_{1}}{G A}=\\ =& \frac{1}{E I}\left[-\frac{1}{3} \cdot 4 \cdot 68 \cdot 4+\frac{1}{3} \cdot 4 \cdot 4 \cdot \frac{6 \cdot 4^{2}}{8}-\frac{1}{3} \cdot 2 \cdot 2 \cdot 10-\frac{1}{2} \cdot 2 \cdot 2 \cdot 10\right]+\\ &+\frac{\kappa}{G A}\left[-\frac{1}{2} \cdot 2 \cdot 29 \cdot 1+\frac{1}{3} \cdot 4 \cdot 5 \cdot 1+2 \cdot 1 \cdot 5\right]=\\ =&-332 \frac{1}{E I}-\frac{124}{3} \frac{\kappa}{G A} \]

Maxwell-Mohr Formula

Now let's see the full form of the Maxwell-Mohr formula, which already takes into account all possible interactions with the structure.


Maxwell-Mohr Formula
\[ \begin{gathered} \Delta_i=\sum_{i_{el}=1}^{n_{el} }\left\{\int_s \frac{\bar{M}_i M_P}{E J} d s+\int_s \frac{\kappa \overline{Q_i} Q_P}{G A} d s+\int_s \frac{\bar{N}_i N_P}{E A} d s\right\}+ \\ +\sum_{i_{el} =1}^{n_{el} }\left\{\frac{\alpha \Delta T}{h} \int_s \bar{M}_i d s+\alpha T_0 \int_s \bar{N}_i d s\right\}+ \\ +\sum_n R_n^P \bar{R}_n f_n-\sum_k \bar{R}_k \Delta_k \end{gathered} \] \(\Delta_i\) - unknown displacement of the point \(i\)

Maxwell-Mohr Formula with described interactions

Influence of internal forces

\[ \sum_{i_{el} =1}^{n_{el} }\left\{\int_s \frac{\bar{M}_i M_P}{E J} d s+\int_s \frac{\kappa \bar{Q}_i Q_P}{G A} d s+\int_s \frac{\bar{N}_i N_P}{E A} d s\right\} \] where:
\( 1) \sum{\int_s \frac{\bar{M}_i M_P}{E J} d s} \) - integration of the graph/function of bending moments on all intervals with the initial state \( M_P \) and the graph/function of bending moments in the unit state \( \overline{M_1} \)

*) initial state - mechanical loads applied in the task such as point loads, concentrated moments, continuous loads
*) unit state - loading of the given system with the single force at the place and in the direction of the required displacement

\( EI \) - flexural rigidity, where:

E - Young's modulus
I - moment of inertia of the section with respect to the bending axis (in simple bending - horizontal axis)

\( 2) \sum{\int_s \frac{\kappa \bar{Q}_i Q_P}{G A} d s} \) - integration of the graph/function of shear forces on all intervals with the initial state \( T_P \) and the graph/function of shear forces in the unit state \( \overline{T_1} \)
\( \kappa \) - shear coefficient,
Rectangle \(\kappa=1.2\)
I-beam \(\quad \kappa=\frac{A}{A_{\text {centroid }}}=\frac{A}{g(h-2 t)}\)

\( GA \) - rigidity to shearing, where:

G - Kirchhoff modulus
A - cross-sectional area

\( 3) \sum{\int_s \frac{\bar{N}_i N_P}{E A} d s } \) - integration of the graph/function of normal forces on all intervals with initial state \( N_P \) and the graph/function of shear forces in the unit state \( \overline{N_1} \)
\( EA \) - rigidity to tension, where:

E - Young's modulus
A - cross-sectional area

Influence of temperature

Non-uniform temperature

\[ \sum_{i_{el}=1}^{n_{el} }\left\{\frac{\alpha \cdot \Delta T}{h} \int_s \bar{M}_i d s\right\} \] where:

\(\alpha \) - thermal expansion coefficient - a material constant dependent on the adopted material, its value is the relative change in the size of the body with a change in temperature of 1 [K];
\( \Delta T \) - difference in temperature between the top and bottom of the bar \( \Delta T = |t_{top} - t_{bottom}| \);
\( t_{top} \) - temperature at the top of the bar;
\( t_{bottom} \) - temperature at the bottom of the bar (it doesn't matter where we assume the top and bottom);
\( h \) - height of the section;
\( \int_s \bar{M}_i d s \) - area on the graph of moments in the unit state on bars loaded with temperature \( \Delta T \), if different bars are loaded with different temperatures, then the coefficient \( \Delta T \) is multiplied separately by the area on the corresponding bar;
The sign of the area is taken as positive if the moment graph is on the side of warmer fibers

Uniform temperature

\[ \sum_{i_{el}=1}^{n_{el} }\left\{\alpha T_0 \int_s \bar{N}_i d s\right\} \] where:

\(\Delta T_0 \) - average temperature minus assembly temperature \(\Delta T_0=\frac{t_{top}+t_{bottom}}{2} - t_m \);
\( \int_s \bar{N}_i d s \) - area on the graph of normal forces in the unit state on bars loaded with temperature \( \Delta T_0 \), if different bars are loaded with different temperatures, then the coefficient \(\Delta T_0 \) is multiplied separately by the area of the normal forces on the corresponding bar;
The sign of the area is taken from the graph - the graph of normal forces is marked

Influence of elastic supports

\[ \sum_n R_n^P \bar{R}_n f_n \] where:

\(R_n^P \) - reaction in state P at the place and in the direction of the elastic constraint
\( \bar{R}_n \) - reaction in the unit state at the place and in the direction of the elastic constraint
\( f_n \) - compliance of the elastic constraint, if linear then in \( \left[ \frac{m}{N} \right] \), if rotational then in \( \left[ \frac{rad}{N\cdot m} \right] \)

Rigidity -> inverse of compliance \( \Rightarrow k=\frac{1}{f} \ \left[ \frac{N}{m} \right] \)

Influence of settlement of supports

\[ - \sum_k \bar{R}_k \Delta_k \]
where:

\(\overline{R_k} \) - reaction in the unit state at the place and in the direction of the imposed displacement
\( \Delta_k \) - value of the imposed displacement

If the imposed displacement is on multiple constraints, then summing is performed - displacement on one constraint (x) reaction in the unit state plus each subsequent displacement (x) corresponding to the reaction in the unit state; the same applies to an elastic constraint