EduPanda Logo

Strength of materials

Clebsch method

  1. Introduction to the Clebsch Method
    • Differential equation of a deformed beam axis
    • Bending stiffness EJ
    • Sign convention
  2. Integrating the differential equation
    • Beam rotation angle function
    • Deflection function
    • Integration constants
    • Boundary conditions
  3. Rules for applying the Clebsch method
    • Uniform coordinate system
    • Continuity of loading
    • Displacement factor
    • Integration method
  4. Computational example
    • Three-span beam
    • Calculating support reactions
    • Moment function
    • Determining integration constants
    • Calculating deflection at a point

Differential equation of the deformed beam axis

The differential equation of the deformed beam axis from which we derive in the Clebsch Method has the following form:

\[ E J \frac{d^2 y}{d x^2}=-M_g \]

The product \(E J\) is a general designation of stiffness in bending, where:

  • E - Young's modulus,
  • J - moment of inertia of the beam cross-section with respect to the horizontal axis.

The sign "-" on the right side of the equation results from the adopted coordinate system and the convention defining the sign of the bending moment. Specifically - the assumption of positive deflections downwards, and thus the positive direction of the deflection axis downwards.

Integrating the differential equation

In order to determine the deflections of the beam, we integrate the above equation twice and obtain the first derivative - the function of the angle of rotation of the beam:

\[ \varphi=\frac{d y}{d x}=-\frac{1}{E J}\left(\int M_g d x+C\right) \]

and the second derivative - the function of deflection:

\[ y=-\frac{1}{E J}\left(\int\left(\int M_g d x\right) d x+C x+D\right) \]

where: C and D denote the constants of integration.

The constants of integration are determined from the kinematic boundary conditions, i.e., conditions for zero deflections and angles of deflection at a specified type of support. See what types of supports there are for a beam in the plane

Rules for applying the Clebsch method

As we have noted the Clebsch method, while maintaining certain conditions of notation, allows for a straight beam to obtain the equation of the deflection line containing only two unknowns (constants of integration) regardless of the number of segments.

The rules governing the application of the Clebsch method can be summarized in 4 points:

1. Uniform coordinate system

The coordinates in all segments must be measured from the same point - we adopt one coordinate system for the straight beam, we cannot write, for example, part of the function from one side and part from the other side of the beam.

2. Continuity of distributed load

In the case of a continuous load acting, it cannot be interrupted - if such a case occurs, the continuous load should be extended to the end of the beam, simultaneously adding the same load with the opposite sign (counter-load).

3. Form of notation for new terms

All newly added terms in the expression for the bending moment must contain the factor \((x- l_{i-1})\), where \(l_{i-1}\) denotes the coordinate of the beginning of the i-th segment of the beam.

In the case of a concentrated moment M – we multiply the moment by the arm of action to the power of 0:

\[ M\cdot (x-l_{i-1})^0 \]

4. Method of integration

Integration should be performed without expanding expressions in parentheses - the constants of integration apply to the entire beam (for all segments).

If the coordinates \(l_{\mathrm{i}}\) define the position of concentrated forces \(P_{\mathrm{i}}\) or the beginnings of continuous load \(q_{\mathrm{i}}\), then expressions of the type \(P_i\left(x-l_i\right)\) or \(q_i \frac{\left(x-l_i\right)^2}{2}\) are integrated according to the scheme:

\[ \int\left(x-l_i\right)^n d x=\frac{\left(x-l_i\right)^{n+1}}{n+1}+C \]

From this course, you will learn:

The Clebsch method (analytical):

  • how to determine the moment function for the beam using the Clebsch method,
  • how to write the differential equation of the deformed axis and how to integrate it,
  • how to calculate the constants of integration from boundary conditions for different types of beams,
  • how to calculate deflection and angle of rotation at any point of the beam.

Statically indeterminate systems:

  • how to determine reactions in a statically indeterminate beam using the Clebsch method.

And now let’s look at the example below and see the solution in practice.

See the example

Three-segment beam with different types of loads.
Calculate the deflection and angle of rotation at a given point of the beam.

Solution of the example from the video course

Content

Calculate the deflection at point A.

Przykład 1 - metoda Clebscha
Fig. 1. Diagram of the beam with loads
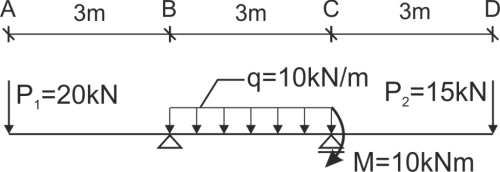
Solution
We calculate the support reactions
Reakcje podporowe
Fig. 2. Diagram with support reactions
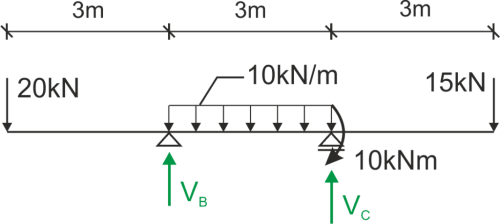\[ \begin{aligned} &\sum{M_B}=0: -20\cdot 3+30\cdot 1.5+10+15\cdot 6-R_C\cdot 3=0 \Rightarrow R_A=28.33kN\\ &\sum{M_C}=0: -20\cdot 6+R_B\cdot 3-30\cdot 1.5+10+15\cdot 3=0 \Rightarrow R_B=36.67kN\\ &\sum{P_iY}=0: -20+R_B-30+R_C-15=0 \Rightarrow L=P \end{aligned} \]
We write the moment function

We write the moment function from the left side. The function can also be written from the right side. We encourage you to check this variant, calculate the sought displacement, and compare the results.

Funkcja momentu
Fig. 3. Determining the moment function
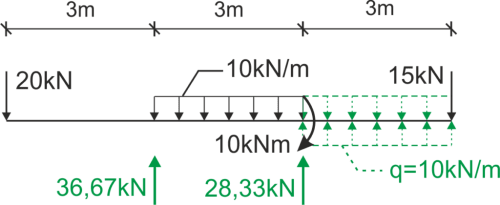\[ \begin{aligned} &M_g(x)=-20x+R_B(x-3)-\frac{1}{2}q(x-3)^2+R_C(x-6)+10(x-6)^0+\frac{1}{2}q(x-6)^2\\ &EJ\cdot w''=-M_g(x)=20x-R_B(x-3)+5(x-3)^2- 28.33(x-6)-10(x-6)^0-5(x-6)^2\\ &EJ\cdot w'=20\frac{x^2}{2}-36.67\frac{(x-3)^2}{2}+5\frac{(x-3)^3}{3}-28.33\frac{(x-6)^2}{2}-10(x-6)-5\frac{(x-6)^3}{3}+C\\ &EJ\cdot w=20\frac{x^3}{6}-36.67\frac{(x-3)^3}{6}+5\frac{(x-3)^4}{12}-28.33\frac{(x-6)^3}{6}-10\frac{(x-6)^2}{2}-5\frac{(x-6)^4}{12}+Cx+D \end{aligned} \]
Boundary conditions
\[ \begin{aligned} &w(x=3)=0 \Rightarrow 90+3C+D=0\\ &w(x=6)=0 \Rightarrow 588.735+6C+D=0\\ &C=-166.245\\ &D=408.735 \end{aligned} \]
We calculate the deflection at point A

If we have adopted the coordinate system at the left end of the beam, then point A has the coordinate x=0.

Therefore:

\[ \begin{aligned} &w_A(x=0)=\frac{1}{EI}\cdot (D)\\ &w_A=\frac{1}{EI}\cdot (408.735) \end{aligned} \]