Types of Supports on a Plane and in 3D Space
- what a support in structural mechanics is
- what the degrees of freedom of movement in a plane are
- what the types of supports in a plane are
a) hinged sliding support
b) hinged non-sliding support
c) truss member/tie/rod
d) fixed support/bracket
e) fixed support with sliding/shoe
f) rotational lock/wedge
- what the types of supports in 3D space are in such systems as:
a) hinged grids,
b) rigid grids,
c) 3D frames,
What is a support in structural mechanics?
A support in structural mechanics is an element that provides a reaction to forces and moments acting on a structure. In the context of engineering and structural design, supports are essential components that enable load transfer, ensure stability and equilibrium of the structure, and allow it to function safely and effectively.The number of independent movements an object can perform in a plane
Different types of supports restrict different movement possibilities in a plane or in space.In a plane, there are three main degrees of freedom of movement:
• Translation along the X-axis: This is movement along the horizontal X-axis, allowing the object to move left or right in the plane.
• Translation along the Y-axis: This is movement along the vertical Y-axis, allowing the object to move up or down in the plane.
• Rotation about the vertical (Z) axis: This is the rotation of the object around an axis perpendicular to the plane, commonly referred to as the Z-axis. This movement allows the object to rotate around the center of the plane.
It is worth noting that degrees of freedom may vary depending on the context and specifics of the structure. For example, a complex mechanism may include additional movements such as tilting or rotation about other axes.
When analyzing the movement of objects in a plane, these three basic degrees of freedom serve as a key reference point.
Types of supports in a plane
Given that in a plane we have three degrees of freedom of movement, supports can remove these degrees of freedom in various combinations. When a support restricts a certain type of movement, such as horizontal movement, a reaction force arises in the support in that direction. First, we will briefly characterize the types of supports in a plane, and then, for greater clarity, we will present in a table the following information regarding planar supports:- a common name/names,
- a graphical symbol/symbols,
- what type of reaction occurs,
- which degree of freedom of movement it removes.
a) hinged sliding support
It blocks linear movement in one direction, allows movement in the perpendicular direction, and also allows rotation. The graphical symbols we encounter in literature are shown below:
Fig.1 Hinged sliding support
The horizontal line under the triangular symbol of the hinged support shows the direction in which movement is possible. The direction perpendicular to the direction of allowed movement is blocked, and a reaction arises in that direction. Of course, a hinged sliding support can be applied at various angles, as shown below:

Fig.2 Hinged sliding support at different angles with indicated reaction
If the support and reaction are at an angle, it is often easier for calculation purposes to resolve this reaction into components:

Fig.3 Decomposition of the reaction into components
After decomposing into components, in calculations we either use the resultant reaction (red) or both components (blue) – never both at the same time. That is, when writing equilibrium equations or determining internal forces, we either use the components or the resultant, not both simultaneously.
b) hinged non-sliding support
In a hinged non-sliding support, there is actually only one reaction, but we do not know its direction. Therefore, it is best to immediately mark two components of this reaction. They do not necessarily have to be vertical and horizontal, but they must be perpendicular to each other. It is also worth noting that the directions of reaction never matter and are just a matter of our assumption. In the figure below, apart from the symbol of the support, the rod emerging from it is shown (of course, the angle at which the rod leaves the support does not matter either).
Fig.4 Hinged non-sliding support
Note! If the emerging rod is also ended with a hinge on the other side, then we are dealing with a truss member/tie/rod about which you can find more information below.
Often, the dilemma about how to mark the reactions arises when we see a non-sliding support rotated at a different angle. It should be remembered that such a support always has two mutually perpendicular reaction components, and it is up to us in which directions we mark these reactions. Each variant shown below is OK.
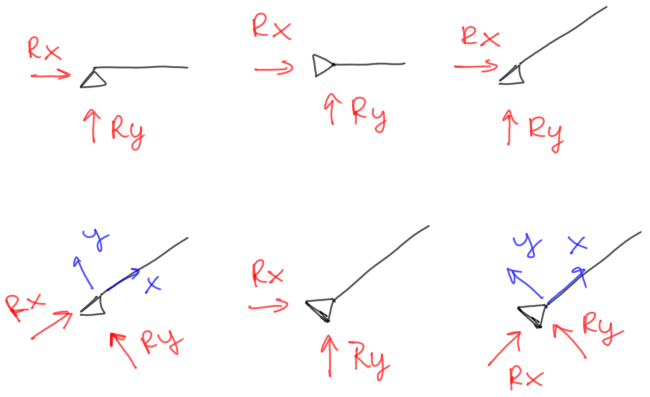
Fig.5 Hinged non-sliding support with indicated reactions
c) truss member/tie/rod
We may encounter a beam/frame supported, for example, by a non-sliding hinged support plus a tie (See free example 1)
Fig.6 Frame system supported by a cable
or a beam supported solely by cables (See free example 2)
Fig.7 Beam supported by three ties
For us to speak of a cable/tie/truss member, the following conditions must be met:
- The member must be terminated at both ends with hinges (these are the member’s nodes),
- The member must be linear (no bends, see the example below),
- There must be no load between the nodes,
- The load can be applied at most at a node (remember that if it is a concentrated moment, it cannot be applied exactly at the hinge, it must be applied on one side or the other of the hinge)
- only axial force (normal force) acts in it,
- there are no shear forces or bending moments.
Below on the left, there is an example of two truss members, on the right, due to the lack of a hinge in the middle, the member is not linear, so we do not have a truss member but a frame system supported by two non-sliding hinged supports.

Fig.8 Example classification of a truss member and a frame system
This is a fundamental difference between these two constructions, and they are calculated completely differently. In hinged supports, we show reactions as shown previously, but when it comes to reactions in a truss member, we have two ways to show the reaction:
1. Cutting through the member and showing internal (axial) forces in the member and discarding the external part of the structure.
2. Showing the reaction at the end of the member, outside the structure, i.e., at the support; the reaction only occurs along the axis of the member.

Fig.9 Second variant of the reaction in a truss member and reactions in a hinged frame system.
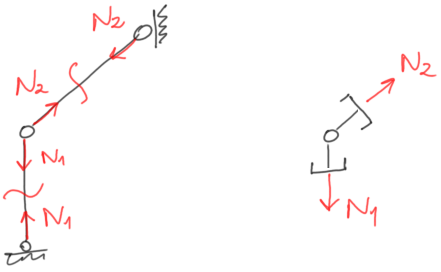
Fig.10 First variant of marking the reaction/forces in a truss member
On our site, you will usually find the first variant because we think it is better.
In the above example:
a) we cut through the member,
b) we show the forces in the member (always either towards each other or away from each other – it’s best to assume as above, i.e. towards each other – then we assume the member is in tension),
c) we discard these parts outside the structure.
d) full fixity/support
A full fixity, commonly known as a fixed support, removes all possible movements in the plane, i.e., both linear movement and rotation. Therefore, it has three reactions: two mutually perpendicular concentrated forces and a concentrated bending moment. As with the non-sliding hinged support, the directions and senses of the reactions are a matter of our assumption (we only remember that the reaction forces should be perpendicular to each other).
Fig.11 Ways of marking a fixed support and the reactions within it
e) fixed support with sliding/shoe
A fixed support with sliding allows linear movement in one direction while blocking linear movement in the perpendicular direction and rotation. We can distinguish between a vertical shoe and a horizontal shoe, but a fixed support with sliding can also be at any angle. Below are several possibilities of marking the shoe along with the reactions within it.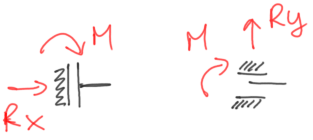
Fig.12 Vertical and horizontal shoes with their reactions

Fig.13 Other possibilities of a fixed support with sliding along with reactions
f) rotational lock/wedge
This type of support is very rarely encountered and usually is not strictly part of a standard exercise set, but we may come across it especially when analyzing a beam/frame using the virtual work method and, of course, in almost every task in the field of structural mechanics – displacement methods.A rotational lock is a constraint that, as the name suggests, blocks only the possibility of rotation of a point (node). We may see such notations of a rotational lock:

Fig.14 Graphical notation of a support/constraint – rotational lock
In this support, there is only a reaction in the form of a bending moment. The node has the freedom to move in every direction but cannot rotate – meaning the shape of the node after displacement must remain the same as before displacement. The first symbol on the left resembles a wedge, and this term might also be used. The third symbol resembles both a vertical and horizontal shoe simultaneously.
Degrees of freedom of movement in 3D space
In three-dimensional space (3D), there are six main degrees of freedom of movement that define the number of independent movements an object can perform. These degrees of freedom are:• Translation along the X-axis,
• Translation along the Y-axis,
• Translation along the Z-axis,
• Rotation about the X-axis,
• Rotation about the Y-axis,
• Rotation about the Z-axis.
All these degrees of freedom together define how an object can move and rotate in 3D space. By understanding this classification, engineers and designers can analyze and model the movements of objects and structures in three dimensions.
Types of supports in 3D space
In a planar system, having 3 degrees of freedom of movement (X translation, Y translation, Z rotation), we managed to identify 6 types of supports depending on the combinations of taken-up degrees of freedom.It will be difficult to conduct a similar classification of supports in 3D space; therefore, we will give general principles regarding supports and the most popular supports in structures such as:
a) hinged grids,
b) rigid grids,
c) 3D frames.
A grid is a planar truss-like structure that is loaded perpendicularly to the plane of the grid’s beams. Depending on the way the beams are connected in the grid, we can distinguish:
a) hinged grids
The beams of the grid are connected by hinges so that they can freely rotate relative to each other. Such a connection only transmits vertical forces (perpendicular to the plane of the grid beams) through the link connecting the beams.Because the grid loading acts perpendicular to the plane of the beams, and since the beams only transmit transverse forces between themselves, in a hinged grid only transverse forces and bending moments occur. This affects what reactions can occur in the supports. Thus, we can distinguish the following supports:
- hinged support
Here it does not matter whether it is drawn as sliding or not – we do not mark reactions in the plane of the grid, only the reaction out of the plane.
Fig.15 Ways of marking a hinged support in a hinged grid
- vertical shoe
Below, a vertical shoe is shown in two directions along with a moment reaction – indicated in two ways – as a moment vector and as a moment on a "small note" – both notations are equivalent. In the shoe, there is no vertical reaction. In grids, we generally ignore reactions along the beam’s axis, so we only have a moment reaction here – it is a bending moment for the member, since hinged grids do not transmit torsion (due to the hinged connections).
Fig.16 Vertical shoe along with reactions for a hinged grid
- full fixity
In a full fixity of a hinged grid, we have a reaction in the form of a bending moment for the beam and a vertical force. Below, the reaction in the form of a moment is indicated in two ways in one figure.
Fig.17 Full fixity along with reactions for a hinged grid
You can find solutions for hinged grid problems in the online course structural mechanics – specifically here. They are part of the subscription (one subscription provides access to materials on the entire site – i.e., all online courses).
b) rigid grids
The beams of the grid are connected to each other rigidly (you can imagine this as if the rods were concreted into each other). Bending beams arranged in one direction causes bending and torsion of the beams arranged in the other direction.In rigid grids, we have the same supports as in hinged grids, but here the difference is that we also deal with torsion. Thus, in full fixity in addition to the bending moment reaction, there will also be a torsional moment reaction. We will also have more shoe options (either blocking bending, or torsion, or both).
Types of supports in rigid grids:
- hinged support
Exactly the same as in a hinged grid. It does not matter whether it is shown as sliding or not – we do not mark reactions in the plane of the grid, only the reaction out of the plane.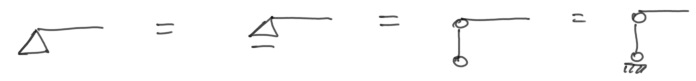
Fig.18 Ways of marking a hinged support in a rigid grid
- vertical shoe
As mentioned before, we have three types of shoes in a rigid grid:- with reaction in the form of a torsional moment,
- with reaction in the form of a bending moment,
- with both of the above.
Here we have another way of marking the shoe than before. Generally, I have not found anywhere in the literature a shoe specifically for rigid grids, but the notation shown below seems reasonable. It also coincides with the notation that appears, for example, in the Robot Structural Analysis program.

Fig.19 Vertical shoes along with reactions for a rigid grid
The first notation can often be used as a full fixity, therefore it is best to clarify if possible what type of support the person who drew the problem had in mind.
- full fixity
If we want to be consistent and apply a similar notation as with the shoe, we should mark full fixity as shown on the left side. However, I think the most popular will still be the simplest notation we encountered before – shown on the right side.
Fig.20 Full fixity in a rigid grid along with reactions
c) 3D frames
In a spatial frame, we have 6 constraints, so the reactions can be taken up by these constraints in various configurations. Most often we will encounter a full fixity and ordinary support members that block movement in the direction in which the member is placed.Below are some possibilities for supports:
- support member/hinged sliding support
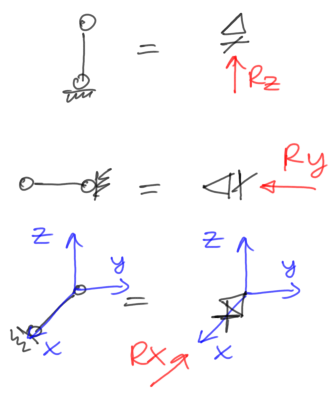
Fig.21 Blocking movement in one direction with reaction
One location can have one, two, or three blocked directions, so now the variant with two blocks in one place:
- support members/hinged sliding support
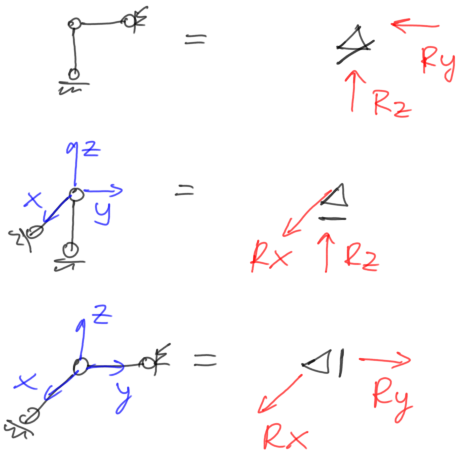
Fig.22 Blocking movement in two directions with reactions
- hinged non-sliding support

Fig.23 Hinged non-sliding support with reactions
- full fixity
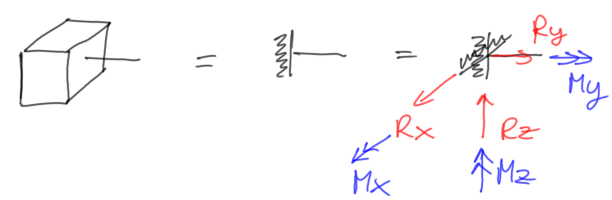
Fig.24 Full fixity with reactions
You will rarely encounter other types of supports than those listed above in spatial systems (I have not come across any). In general, in principle, any direction of linear or rotational movement can be blocked in any combination, for example:

Fig.25 Various combinations of blocking linear and rotational movement with reactions
and so on.