Rodzaje podpór na płaszczyźnie
i w przestrzeni 3D

Z tego tekstu dowiesz się:
- czym jest podpora w mechanice konstrukcji
- jakie mamy stopnie swobody ruchu na płaszczyźnie
- jakie mamy rodzaje podpór na płaszczyźnie

a) podpora przegubowa przesuwna
b) podpora przegubowa nieprzesuwna
c) pręt kratowy/cięgno/linka
d) utwierdzenie pełne/wspornik
e) utwierdzenie z przesuwem/łyżwa
f) blokada obrotu/klin

- jakie mamy stopnie swobody ruchu w przestrzeni 3D
- jakie mamy rodzaje podpór w przestrzeni 3D w takich układach jak:

a) ruszty przegubowe,
b) ruszty sztywne,
c) ramy 3D,

- czym są kinematyczne warunki brzegowe i gdzie z nich korzystamy
- jak zapisać warunki brzegowe w zapisie różnicowym (metoda różnic skończonych)

Znajdziesz również przykłady obliczeniowe, ponieważ tak na prawdę każde zadanie z belek, ram, kratownic zaczyna się od zaznaczenia reakcji w podporach oraz ich obliczenia.

↓ odnośnik do bazy zadań z rozwiązaniami oraz do kursów wideo ↓

Zobacz wideo-kurs z tego działu!
obliczanie reakcji podporowych (i nie tylko)
w BELKACH prostych Zobacz wideo-kurs z tego działu!
obliczanie reakcji podporowych (i nie tylko)
w RAMACH prostych Zobacz zadania z tego działu!
obliczanie reakcji podporowych (i nie tylko)
w BELKACH prostych Zobacz zadania z tego działu!
obliczanie reakcji podporowych (i nie tylko)
w RAMACH z prętem skośnym

Są to tylko przykładowe materiały, o wiele więcej znajdziesz wchodząc na główną stronę wytrzymałości materiałów w działach: siły wewnętrzne -> belki, ramy, kratownice, łuki, układy złożone oraz rozciąganie i ściskanie osiowe -> układy prętów, a także w dziale ze Zginania, Ugięć, Metod energetycznych, Hipotez wytężeniowych.

A teraz do rzeczy!

Czym jest podpora w mechanice konstrukcji?

Podpora w mechanice konstrukcji to element, który zapewnia reakcję na siły i momenty działające na strukturę lub konstrukcję. W kontekście inżynierii i projektowania konstrukcji, podpory są istotnymi komponentami, które umożliwiają przenoszenie obciążeń, zapewniają stabilność i równowagę struktury oraz umożliwiają jej funkcjonowanie w sposób bezpieczny i efektywny.

Liczba niezależnych ruchów, jakie obiekt może wykonać na płaszczyźnie

Różne rodzaje podpór ograniczają różne możliwości ruchu na płaszczyźnie lub w przestrzeni.
Na płaszczyźnie istnieją trzy główne stopnie swobody ruchu:

• Translacja wzdłuż osi X: To ruch wzdłuż poziomej osi X, który pozwala obiektowi przemieszczać się na płaszczyźnie w lewo lub w prawo.

• Translacja wzdłuż osi Y: To ruch wzdłuż pionowej osi Y, który pozwala obiektowi przemieszczać się na płaszczyźnie w górę lub w dół.

• Obrót wokół osi pionowej (Z): To ruch obracania się obiektu wokół osi prostopadłej do płaszczyzny, nazywanej zazwyczaj osią Z. Ten ruch pozwala obiektowi obracać się wokół środka płaszczyzny.

Warto zauważyć, że stopnie swobody mogą się różnić w zależności od kontekstu i specyfiki konstrukcji. Przykładowo, stopnie swobody mechanizmu skomplikowanego mogą obejmować dodatkowe ruchy, takie jak pochylenie czy obrót wokół innych osi.
W przypadku analizy ruchu obiektów na płaszczyźnie, te trzy podstawowe stopnie swobody stanowią kluczowy punkt odniesienia.

Rodzaje podpór na płaszczyźnie

Wobec tego, że na płaszczyźnie mamy trzy stopnie swobody ruchu, podpory mogą odbierać te stopnie swobody w różnych kombinacjach. Zabranie przez podporę możliwości ruchu np. poziomego wiąże się z powstaniem w podporze reakcji w tymże kierunku. Najpierw krótko scharakteryzujemy rodzaje podpór na płaszczyźnie, a następnie dla większej przejrzystości zestawimy w tabeli następujące informacje dotyczące podpór na płaszczyźnie:
- popularną nazwę/nazwy,
- graficzny symbol/symbole,
- jaka występuje w niej reakcja,
- jaki stopień swobody ruchu zabiera.

a) podpora przegubowa przesuwna

Blokuje możliwość ruchu liniowego w jednym kierunku, zezwaja na ruch w kierunku prostopadłym do blokowanego oraz na obrót. Oznaczenia graficzne z jakimi się spotkamy w literaturze:

Rys1. Podpora przegubowa przesuwna

Pozioma kreska pod trójkątnym symbolem podpory przegubowej pokazuje w jakim kierunku jest możliwość ruchu. Zablokowany jest kierunek prostopadły do możliwości ruchu i w tym kierunku powstaje reakcja. Oczywiście podpora przegubowa może być stosowana pod różnymi kątami, jak poniżej:

Rys2. Podpora przegubowa przesuwna pod innymi kątami z zaznaczoną reakcją

Jeśli podpora oraz reakcja są pod kątem to często dla uproszczenia obliczeń będzie nam wygodniej rozłożyć tą reakcję na składowe:

Rys3. Rozłożenie reakcji na składowe

Po rozłożeniu na składowe w obliczeniach korzystamy albo z jednej, wypadkowej reakcji (czerwona) albo z obu składowych (niebieskie) – nigdy z obydwóch na raz. To znaczy zapisując równanie równowagi statycznej albo określając siły wewnętrzne wykorzystujemy albo składowe albo wypadkową reakcję.

b) podpora przegubowa nieprzesuwna

W podporze przegubowej nieprzesuwnej też występuje tak naprawdę jedna reakcja, jednak nie znamy jej kierunku. Dlatego najlepiej od razu zaznaczać dwie składowe tej reakcji. Nie muszą one być koniecznie pionowo i poziomo, ale muszą być do siebie prostopadłe. Warto wspomnieć też, że zwroty reakcji nigdy nie mają znaczenia i są tylko kwestią naszego założenia. Na poniższym rysunku zaznaczono oprócz samego symbolu podpory wychodzący z niej pręt (oczywiście nie ma też znaczenia pod jakim kątem pręt wychodzi z podpory)

Rys4. Podpora przegubowa nieprzesuwna

Uwaga! Jeżeli wychodzący pręt będzie dodatkowo zakończony przegubem również z drugiej strony, wówczas mamy do czynienia z prętem kratowym/cięgnem/linką o której więcej informacji znajdziesz niżej.

Często dylemat odnośnie zaznaczenia reakcji pojawia się kiedy zobaczymy podporę nieprzesuwną obróconą pod różnym kątem. Należy pamiętać, że w podporze takiej mamy zawsze dwie prostopadłe do siebie reakcje i to od nas zależy w jakich kierunkach te reakcje zaznaczymy. Każdy pokazany poniżej wariant jest OK.

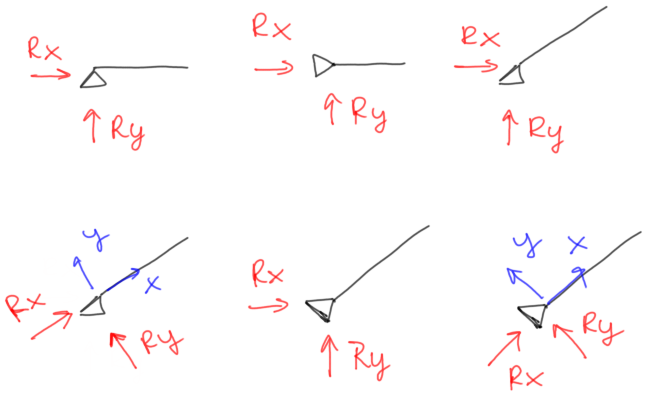
Rys5. Podpora przegubowa nieprzesuwna z zaznaczonymi reakcjami

c) pręt kratowy/cięgno/linka

Możemy spotkać się na przykład z takim podparciem belki/ramy – podpora przegubowa nieprzesuwna + podczepienie linką (Zobacz darmowy przykład 1 )

Rys6. Układ ramowy podczepiony linką

albo z podczepieniem belki na samych linkach. (Zobacz darmowy przykład 2 )

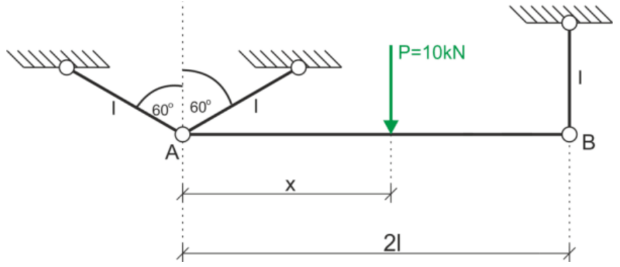
Rys7. Belka podczepiona na trzech cięgnach

Żebyśmy mogli mówić o lince/cięgnie/pręcie kratowym muszą być spełnione poniższe założenia:

- pręt musi być zakończony z obydwóch stron przegubami (są to węzły pręta),
- pręt musi być liniowy (nie może być załamań, patrz przykład poniżej),
- nie może być obciążenia między węzłami,
- obciążenie może być co najwyżej przyłożone do węzła (przy czym pamiętajmy, że jeśli jest to moment skupiony to nie może on być przyłożony stricte do przegubu, musi być przyłożony z jednej albo drugiej strony przegubu)

Pręt kratowy przede wszystkim charakteryzuje się tym, że:

- występuje w nim tylko siła osiowa (normalna),
- nie występują w nim siły tnące i momenty zginające.

Poniżej po lewej stronie przykład dwóch prętów kratowych, po prawej z uwagi na brak przegubu w środku pręt nie jest liniowy, więc nie mamy do czynienia z prętem kratowym a z układem ramowym podpartym dwoma podporami przegubowymi nieprzesuwnymi.

Rys8. Przykład klasyfikacji pręta kratowego i układu ramowego

Jest to zasadnicza różnica między tymi dwoma konstrukcjami i liczy się je zupełnie inaczej. W podporach przegubowych pokazujemy reakcje tak jak zostało to pokazane wcześniej, natomiast jeśli chodzi o reakcje w pręcie kratowym to mamy dwie możliwości zaznaczenia reakcji

1. Przecięcie pręta i pokazanie sił wewnętrznych w pręcie (osiowych) i odrzucenie części na zewnątrz konstrukcji
2. Pokazanie reakcji na końcu pręta, na zewnątrz konstrukcji, czyli przy podparciu; reakcja występuje tylko w osi pręta

Rys9. Wariant drugi reakcji w pręcie kratowym oraz reakcje w układzie ramowym przegubowo podpartym.

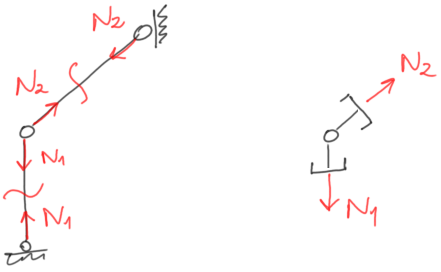
Rys10. Pierwszy wariant zaznaczenia reakcji/sił w pręcie kratowym

Na naszej stronie znajdziecie raczej ten pierwszy wariant, ponieważ wydaje nam się on lepszy
W przypadku powyżej:

a) przecinamy przez pręt,
b) pokazujemy siły w pręcie (zawsze albo do siebie albo od siebie – najlepiej przyjmować jak powyżej czyli do siebie – wtedy zakładamy że pręt jest rozciągany),
c) odrzucamy te części na zewnątrz konstrukcji.

Dla tego przykładu operacja ta sprowadza nam ten układ do równowagi węzła.

d) utwierdzenie pełne/wspornik

Utwierdzenie pełne, czyli popularny wspornik zabiera wszystkie możliwości ruchu na płaszczyźnie, a więc możliwość ruchu liniowego oraz możliwość obrotu. Występują w nim więc trzy reakcje, dwie prostopadłe do siebie reakcje w postaci sił skupionych oraz skupiony moment zginający. Tak samo jak w przypadku podpory przegubowe nieprzesuwnej kierunki i zwroty reakcji są kwestią naszego założenia (pamiętamy tylko, żeby reakcje skupione były do siebie prostopadłe).

Rys11. Sposoby zaznaczenia wspornika oraz reakcji w nim

e) utwierdzenie z przesuwem/łyżwa

Utwierdzenie z przesuwem pozwala na ruch liniowy w jednym kierunku, blokując jednocześnie ruch liniowy w kierunku prostopadłym oraz obrót. Możemy wyróżnić łyżwę pionową oraz poziomą, ale utwierdzenie z przesuwem może być równie dobrze pod dowolnym kątem, poniżej kilka możliwości zaznaczenia łyżwy wraz z reakcjami w niej.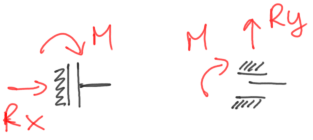

Rys12. Łyżwa pionowa i pozioma wraz z reakcjami w nich

Rys13. Inne możliwości utwierdzenia z przesuwem wraz z reakcjami

f) blokada obrotu/klin

Jest to rodzaj podpory który jest bardzo rzadko spotykany i raczej nie jest nanoszony stricte w temacie zadania, ale możemy na niego trafić najczęściej rozwiązując belkę/ramę zasadą prac wirtualnych oraz oczywiście mamy z nią do czynienia prawie w każdym zadaniu działu mechaniki budowli – metody przemieszczeń.

Blokada obrotu jest to więź która blokuje, jak sama nazwa mówi, jedynie możliwość obrotu punktu (węzła). Możemy spotkać takie oznaczenia blokady obrotu:

Rys14. Graficzne oznaczenie podpory/więzi – blokada obrotu

W tej podporze występuje tylko reakcja w postaci momentu zginającego, węzeł ma swobodę ruchu w każdym kierunku, ale nie może się obrócić – to znaczy kształt węzła po przemieszczeniu musi być taki sam jak przed przemieszczeniem. Pierwsze z lewej oznaczenie graficzne przypomina klin i z taką nazwą tej więzi też możemy się spotkać. Trzecie oznaczenie zaś przypomina łyżwę jednocześnie i pionową i poziomą.

Stopnie swobody ruchu w przestrzeni 3D

W przestrzeni trójwymiarowej (3D) istnieje sześć głównych stopni swobody ruchu, które określają liczbę niezależnych ruchów, jakie obiekt może wykonać. Oto te stopnie swobody:

• Translacja wzdłuż osi X,

• Translacja wzdłuż osi Y,

• Translacja wzdłuż osi Z,

• Obrót wokół osi X,

• Obrót wokół osi Y,

• Obrót wokół osi Z.

Wszystkie te stopnie swobody razem definiują, w jaki sposób obiekt może poruszać się i obracać w przestrzeni 3D. Dzięki tej klasyfikacji, inżynierowie i projektanci są w stanie analizować i modelować ruchy obiektów oraz konstrukcji w trzech wymiarach.

Rodzaje podpór w przestrzeni 3D

W układzie płaskim mając 3 stopnie swobody ruchu (translacja X, translacja Y, obrót Z) zdołaliśmy wyszczególnić 6 rodzajów podpór w zależności od tego w jakich kombinacjach podpory zabierały dopuszczalne swobody ruchu.
Ciężko będzie przeprowadzić klasyfikację podpór w przestrzeni 3D, w związku z tym podamy poniżej raczej ogólne zasady odnośnie podpór i najpopularniejsze podpory w konstrukcjach takich jak:

a) ruszty przegubowe,
b) ruszty sztywne,
c) ramy 3D.

Rusztem nazywamy płaską konstrukcję prętową, która jest obciążona prostopadle do płaszczyzny belek rusztu. Ze względu na sposób połączenia belek rusztu możemy wyróżnić:

a) ruszty przegubowe

Belki rusztu połączone są ze sobą przegubowo, w sposób który pozwala im na swobodny obrót względem siebie. Takie połączenie pozwala tylko na przenoszenie przez wahacz łączący belki siły pionowej (prostopadłej do płaszczyzny belek rusztu).
Ponieważ obciążenie rusztu działa w kierunku prostopadłym do płaszczyzny belek oraz z uwagi na to że belki między sobą przekazują tylko siłę poprzeczną, to w ruszcie przegubowym występują tylko siły poprzeczne i momenty zginające. Ma to wpływ na to jakie reakcje mogą występować w podporach, i tak wyróżnić możemy takie podpory jak:

- podpora przegubowa

Przy czym nie ma znaczenia tutaj czy jest ona narysowana jako przesuwna, czy nie – i tak nie zaznaczamy reakcji w płaszczyźnie rusztu, jedynie reakcję z płaszczyzny.

Rys15. Sposoby zaznaczenia podpory przegubowej w ruszcie przegubowym

- łyżwa pionowa

Poniżej łyżwa pionowa zaznaczona w dwóch kierunkach wraz z reakcją w postaci momentu – który zaznaczono na dwa sposoby – w postaci wektora momentu oraz w postaci momentu na „karteczce” – oba zapisy są sobie równoważne. W łyżwie nie ma reakcji pionowej, w rusztach ogólnie pomijamy reakcje w osi belek, więc mamy tutaj tylko reakcję w postaci momentu – i jest to moment zginający dla pręta, ponieważ ruszty przegubowe nie przenoszą skręcania (z uwagi na połączenia przegubowe).

Rys16. Łyżwa pionowa wraz z reakcjami dla rusztu przegubowego

- utwierdzenie pełne

W utwierdzeniu przy ruszcie przegubowym mamy reakcję w postaci momentu zginającego dla belki oraz siły pionowej. Poniżej zaznaczono reakcję w postaci momentu na jednym rysunku na dwa sposoby

Rys17. Utwierdzenie pełne wraz z reakcjami dla rusztu przegubowego

Rozwiązania zadań z rusztów przegubowych znajdziesz w Kursie online mechanika budowli – konkretnie w tym miejscu, są one objęte abonamentem (jeden abonament zapewnia dostęp do materiałów na całej stronie – tzn. do wszystkich kursów online).

b) ruszty sztywne

Belki rusztu połączone są ze sobą sztywno (można to sobie wyobrazić tak jakby pręty były zabetonowane jeden w drugim). Zginanie prętów ułożonych w jednym kierunku powoduje zginanie i skręcanie prętów w drugim kierunku.

W rusztach sztywnych mamy te same podpory co w rusztach przegubowych, jednak tutaj różnica jest taka, że mamy również do czynienia ze skręcaniem, więc w utwierdzeniu oprócz reakcji w postaci momentu zginającego będzie również reakcja w postaci momentu skręcającego. Będziemy mieli również więcej opcji łyżw (albo blokuje zginanie, albo skręcanie albo jedno i drugie).

Rodzaje podpór w rusztach sztywnych:

- podpora przegubowa

Dokładnie tak samo jak w ruszcie przegubowym. Nie ma znaczenia czy jest ona narysowana jako przesuwna, czy nie – i tak nie zaznaczamy reakcji w płaszczyźnie rusztu, jedynie reakcję z płaszczyzny.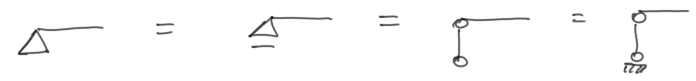

Rys18. Sposoby zaznaczenia podpory przegubowej w ruszcie sztywnym

- łyżwa pionowa

Jak wspomniano wcześniej mamy trzy rodzaje łyżw przy ruszcie sztywnym:

- z reakcją w postaci momentu skręcającego,
- z reakcją w postaci momentu zginającego,
- z jedną i drugą wymienioną powyżej.

I tutaj mamy inny sposób zaznaczenia łyżwy niż wcześniej, generalnie to w literaturze nie udało mi się znaleźć nigdzie łyżwy dla rusztu sztywnego, ale to oznaczenie pokazane poniżej wydaje się być sensowne, pokrywa się też z oznaczeniem które występuje np. w programie Robot Structural Analysis.

Rys19. Łyżwy pionowe wraz z reakcjami poniżej dla rusztu sztywnego

No i cóż, to pierwsze oznaczenie często może być użyte jako utwierdzenie pełne, dlatego najlepiej doprecyzować jeśli jest taka możliwość jaki rodzaj podpory ma na myśli osoba która rysowała temat zadania.

- utwierdzenie pełne

Jeśli chcielibyśmy konsekwentnie zastosować oznaczenie podobne jak przy łyżwie to należałoby zaznaczyć utwierdzenie pełne w sposób pokazany po lewej stronie, jednak myślę że i tak najpopularniejsze będzie to najprostsze oznaczenie z którym się spotkaliśmy wcześniej – zaprezentowane po prawej stronie

Rys20. Utwierdzenie pełne w ruszcie sztywnym wraz z reakcjami

c) ramy 3D

W ramie przestrzennej mamy 6 więzi, więc reakcje mogę odbierać te więzi w różnych konfiguracjach. Najczęściej będziemy mieli do czynienia z utwierdzeniem pełnym oraz ze zwykłymi prętami podporowymi odbierającymi możliwość ruchu w kierunku w którym jest postawiony pręt.

- pręt podporowy/podpora przegubowa przesuwna

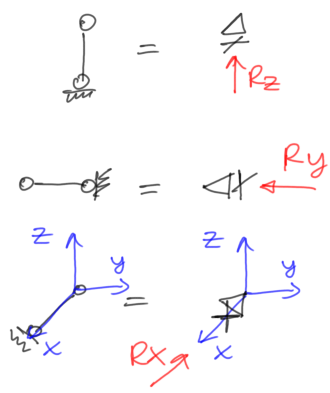
Rys21. Blokada ruchu w jednym kierunku wraz z reakcją

W jednym miejscu może być jeden, dwa lub trzy kierunki zablokowane, więc teraz wariant z dwoma blokadami w jednym miejscu

- pręty podporowe/podpora przegubowa przesuwna

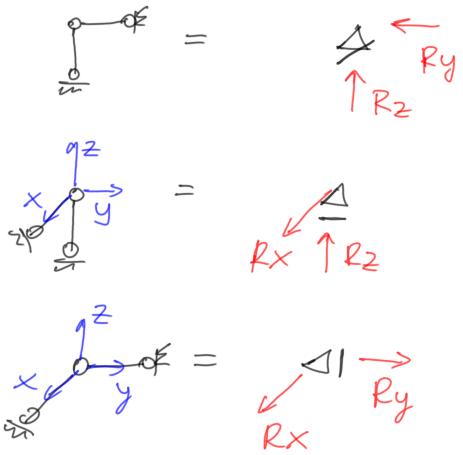
Rys22. Blokada ruchu w dwóch kierunkach wraz z reakcjami

- podpora przegubowa nieprzesuwna

Rys23. Podpora przegubowa nieprzesuwna wraz z reakcjami

- utwierdzenie pełne

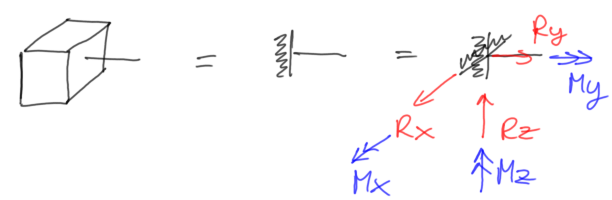
Rys24. Utwierdzenie pełne wraz z reakcjami

Z innym rodzajem podpory niż wymienione powyżej w układach przestrzennych raczej się nie spotkacie (mi się nie zdarzyło), generalnie, co do zasady, może być też zablokowany w dowolnej kombinacji któryś kierunek ruchu i możliwość obrotu w którymś kierunku, na przykład

Rys25. Różne kombinacje blokad ruchu liniowego i obrotu wraz z reakcjami

i tym podobne.

Czym są kinematyczne warunki brzegowe i gdzie z nich korzystamy

Więcej informacji wkrótce.

Warunki brzegowe w zapisie różnicowym (metoda różnic skończonych)

Więcej informacji wkrótce.


↓ odnośnik do bazy zadań z rozwiązaniami oraz do kursów wideo ↓

Zobacz wideo-kurs z tego działu!
obliczanie reakcji podporowych (i nie tylko)
w BELKACH prostych Zobacz wideo-kurs z tego działu!
obliczanie reakcji podporowych (i nie tylko)
w RAMACH prostych Zobacz zadania z tego działu!
obliczanie reakcji podporowych (i nie tylko)
w BELKACH prostych Zobacz zadania z tego działu!
obliczanie reakcji podporowych (i nie tylko)
w RAMACH z prętem skośnym

-> ZOBACZ DOSTĘPNE PLANY<-

Zobacz ofertę i cenę korepetycji

Łukasz Cichowicz Tel: +48 780 155 029 E-mail: lukasz@edupanda.pl Skype: edupandapl