Solution
See theoretical introduction to the Maxwell-Mohr method! It also includes references to more problems and materials on this topic!
Learn more about integration using the Wereszczagin method.
Task solution:
\begin{array}{lcc}
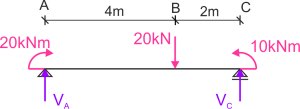
\sum M_{A}=0 & 20-10-6 V_{C}+20 \cdot 4=0 & V_{C}=15 k N \\
\sum M_{C}=0 & 20-10-20 \cdot 2+6 V_{A}=0 & V_{A}=5 k N \\
\sum Y=0 & V_{A}+V_{C}-20=0 & \mathrm{~L}=P
\end{array}
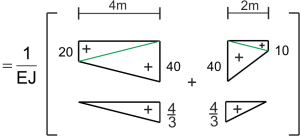 \begin{aligned}
=\frac{1}{E J}\left[\frac{1}{6} \cdot 20 \cdot \frac{4}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{4}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{4}{3} \cdot 2+\frac{1}{6} \cdot 10 \cdot \frac{4}{3} \cdot 2\right]=\frac{128.89}{E J}
\end{aligned}
\begin{aligned}
=\frac{1}{E J}\left[\frac{1}{6} \cdot 20 \cdot \frac{4}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{4}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{4}{3} \cdot 2+\frac{1}{6} \cdot 10 \cdot \frac{4}{3} \cdot 2\right]=\frac{128.89}{E J}
\end{aligned}
 \begin{aligned}
=\frac{1}{E J}\left[-\frac{1}{6} \cdot 20 \cdot \frac{2}{3} \cdot 4-\frac{1}{3} \cdot 40 \cdot \frac{2}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{1}{3} \cdot 2+\frac{1}{6} \cdot 10 \cdot \frac{1}{3} \cdot 2\right]=-\frac{34.44}{E J}
\end{aligned}
\begin{aligned}
=\frac{1}{E J}\left[-\frac{1}{6} \cdot 20 \cdot \frac{2}{3} \cdot 4-\frac{1}{3} \cdot 40 \cdot \frac{2}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{1}{3} \cdot 2+\frac{1}{6} \cdot 10 \cdot \frac{1}{3} \cdot 2\right]=-\frac{34.44}{E J}
\end{aligned}
Learn more about integration using the Wereszczagin method.
Task solution:
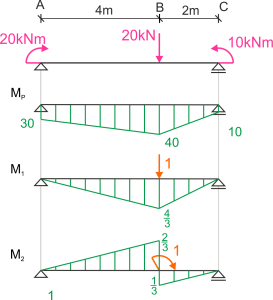
1. Drawing a diagram of moments against external load (Mp) and unit moment diagrams M1 - beam loaded with concentrated force (to calculate vertical displacement) and M2 - beam loaded with concentrated moment (to calculate rotation angle).

2. Displacement of point B vertically
\begin{aligned} \Delta_{B}=\int \frac{M_{P} \cdot M_{1}}{E J} d x= \end{aligned}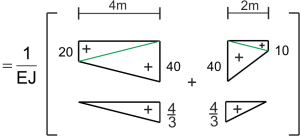 \begin{aligned}
=\frac{1}{E J}\left[\frac{1}{6} \cdot 20 \cdot \frac{4}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{4}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{4}{3} \cdot 2+\frac{1}{6} \cdot 10 \cdot \frac{4}{3} \cdot 2\right]=\frac{128.89}{E J}
\end{aligned}
\begin{aligned}
=\frac{1}{E J}\left[\frac{1}{6} \cdot 20 \cdot \frac{4}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{4}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{4}{3} \cdot 2+\frac{1}{6} \cdot 10 \cdot \frac{4}{3} \cdot 2\right]=\frac{128.89}{E J}
\end{aligned}
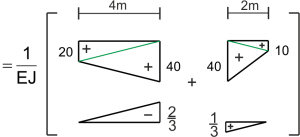
3. Rotation angle at point B
\begin{aligned} \varphi_{B}=\int \frac{M_{P} \cdot M_{2}}{E J} d x= \end{aligned} \begin{aligned}
=\frac{1}{E J}\left[-\frac{1}{6} \cdot 20 \cdot \frac{2}{3} \cdot 4-\frac{1}{3} \cdot 40 \cdot \frac{2}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{1}{3} \cdot 2+\frac{1}{6} \cdot 10 \cdot \frac{1}{3} \cdot 2\right]=-\frac{34.44}{E J}
\end{aligned}
\begin{aligned}
=\frac{1}{E J}\left[-\frac{1}{6} \cdot 20 \cdot \frac{2}{3} \cdot 4-\frac{1}{3} \cdot 40 \cdot \frac{2}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{1}{3} \cdot 2+\frac{1}{6} \cdot 10 \cdot \frac{1}{3} \cdot 2\right]=-\frac{34.44}{E J}
\end{aligned}
If you have any questions, comments, or think you have found a mistake in this solution, please send us a message at kontakt@edupanda.pl.