Solution
Degree of static indeterminacy
$$
\mathrm{SSD} = \mathrm{r} - 3 - \mathrm{p} + 3 \cdot \mathrm{a}
$$
where:
r - reactions
p - hinges
a - closed circuits
\( \mathrm{SSD} = 3 - 3 - 2 + 3 \cdot 1 = 1 \)
Number of degrees of dynamic freedom
\( \mathrm{LSSD} = 3 \\ \quad \mathrm{~m}_1 = 100 \ kg \\ \quad \mathrm{~m}_2 = 100 \ kg \\ \quad \mathrm{~m}_3 = 250 \ kg
\)
assuming
\( \mathrm{m} = 100 \ kg \)
\( m_1 = m, \\ m_2 = m, \\ m_3 = 2.5m \)
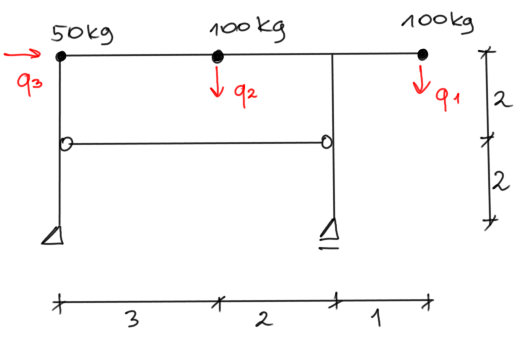
We will solve the frame with the METHOD OF FORCES.
Basic system of the force method
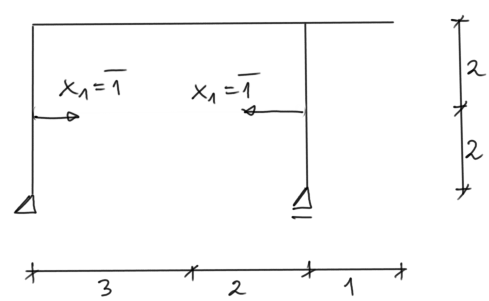
Common unit state
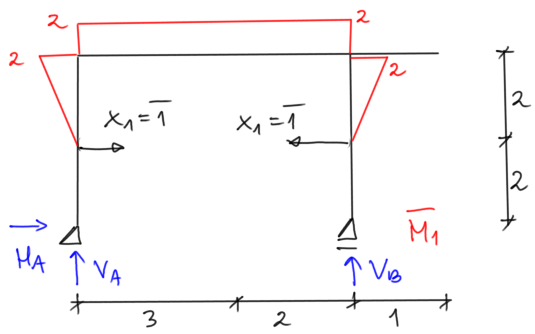
Reactions
$$ \begin{aligned} &\Sigma \mathrm{M}_{\mathrm{A}} = 0 \quad 1 \cdot 2-1 \cdot 2-\mathrm{V}_{\mathrm{B}} \cdot 5 = 0 \quad \mathrm{~V}_{\mathrm{B}} = 0 \\ &\delta_{11} = \frac{1}{\mathrm{EI}} \cdot\left(\frac{1}{3} 2 \cdot 2 \cdot 2+2 \cdot 5 \cdot 2+\frac{1}{3} 2 \cdot 2 \cdot 2\right) = \frac{76}{3} \cdot \frac{1}{\mathrm{EI}} \end{aligned} $$ Now we do parallel analysis for all load cases, calculate the integration of δ1p separately for each case, calculate x1 (solving the canonical equation) and draw the final charts.
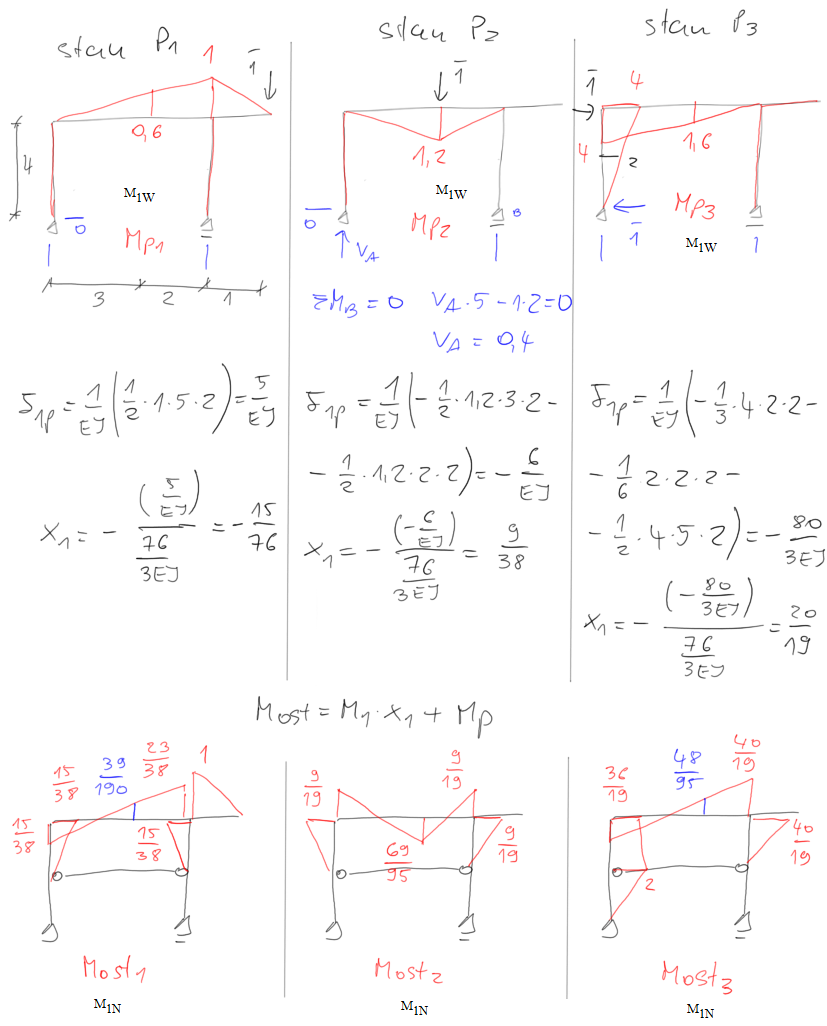
Dynamic deltas from the reduction theorem $$ \begin{aligned} &\delta_{11}=\int \frac{\mathrm{M}_{\mathrm{Ost} 1} \cdot \mathrm{M}_{\mathrm{P} 1}}{\mathrm{EI}} \mathrm{dS} \\ &\delta_{11}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{5}{6} \cdot\left(2 \cdot 1 \cdot \frac{23}{38}-1 \cdot \frac{15}{38}\right)+\frac{1}{3} \cdot 1 \cdot 1 \cdot 1\right]=\frac{77}{76} \cdot \frac{1}{\mathrm{EI}} \end{aligned} $$ $$ \begin{aligned} &\delta_{22}=\int \frac{\mathrm{M}_{\mathrm{Ost} 2} \cdot \mathrm{M}_{\mathrm{P} 2}}{\mathrm{EI}} \mathrm{dS} \\ &\delta_{22}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{3}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{69}{95}-1.2 \cdot \frac{9}{19}\right)+\frac{2}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{69}{95}-1.2 \cdot \frac{9}{19}\right)\right]=\frac{93}{95} \cdot \frac{1}{\mathrm{EI}} \end{aligned} $$ $$ \begin{aligned} &\delta_{33}=\int \frac{\mathrm{M}_{\mathrm{Ost} 3} \cdot \mathrm{M}_{\mathrm{P} 3}}{\mathrm{EI}} \mathrm{dS} \\ &\delta_{33}=\frac{1}{\mathrm{EI}} \cdot\left[\begin{array}{l} \frac{1}{3} \cdot 2 \cdot 2 \cdot 2+\frac{2}{6} \cdot\left(2 \cdot 2 \cdot 2+2 \cdot \frac{36}{19} \cdot 4+\frac{36}{19} \cdot 2+4 \cdot 2\right) \ldots \\ +\frac{5}{6} \cdot\left(2 \cdot 4 \cdot \frac{36}{19}-4 \cdot \frac{40}{19}\right) \end{array}\right]=\frac{1136}{57} \cdot \frac{1}{\mathrm{EI}} \end{aligned} $$ $$ \begin{aligned} &\delta_{12}=\int \frac{\mathrm{M}_{\mathrm{Ost} 1} \cdot \mathrm{M}_{\mathrm{P} 2}}{\mathrm{EI}} \mathrm{dS} \\ &\delta_{12}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{3}{6} \cdot\left(-2 \cdot 1.2 \cdot \frac{39}{190}+1.2 \cdot \frac{15}{38}\right)-\frac{2}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{39}{190}+1.2 \cdot \frac{23}{38}\right)\right]=-\frac{79}{190} \cdot \frac{1}{\mathrm{EI}} \quad \delta_{21}=\delta_{12} \end{aligned} $$ $$ \begin{aligned} &\delta_{13}=\int \frac{\mathrm{M}_{\mathrm{Ost} 3} \cdot \mathrm{M}_{\mathrm{P} 1}}{\mathrm{EI}} \mathrm{dS} \\ &\delta_{13}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{5}{6} \cdot\left(2 \cdot 1 \cdot \frac{40}{19}-1 \cdot \frac{36}{19}\right)\right]=\frac{110}{57} \cdot \frac{1}{\mathrm{EI}} \quad \delta_{31}=\delta_{13} \\ &\delta_{23}=\int \frac{\mathrm{M}_{\mathrm{Ost} 3} \cdot \mathrm{M}_{\mathrm{P} 2}}{\mathrm{EI}} \mathrm{dS} \\ &\delta_{23}=\frac{1}{\mathrm{EI}}\left[\frac{3}{6} \cdot\left(-2 \cdot 1.2 \cdot \frac{48}{95}+1 \cdot 2 \cdot \frac{36}{19}\right)-\frac{2}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{48}{95}+1.2 \cdot \frac{40}{19}\right)\right]=-\frac{68}{95} \cdot \frac{1}{\mathrm{EI}} \quad \delta_{32}=\delta_{23} \end{aligned} $$ assuming \( \mathrm{m}=100 \mathrm{~kg} \quad \mathrm{~m}_1=1 \mathrm{~m} \quad \mathrm{~m}_2=1 \mathrm{~m} \quad \mathrm{~m}_3=2.5 \mathrm{~m} \)
\( \left[\begin{array}{ccc} 1 \cdot \frac{77}{76}-x & 1 \cdot\left(-\frac{79}{190}\right) & \frac{5}{2} \cdot \frac{110}{57} \\ 1 \cdot\left(-\frac{79}{190}\right) & 1 \cdot \frac{93}{95}-x & \frac{5}{2}\left(\frac{68}{95}\right) \\ 1 \cdot \frac{110}{57} & 1 \cdot\left(\frac{68}{95}\right) & \frac{5}{2} \cdot \frac{1136}{57}-x \end{array}\right]=0 \)
\( \left[\begin{array}{llc} \frac{77}{76}-\mathrm{x} & -\frac{79}{190} & \frac{275}{57} \\ -\frac{79}{190} & \frac{93}{95}-\mathrm{x} & -\frac{34}{19} \\ \frac{110}{57} & -\frac{68}{95} & \frac{2840}{57}-\mathrm{x} \end{array}\right]=0 \)
Then you need to use the Sarrus method to calculate the determinant of the above 3x3 matrix and simplify it to a 3rd degree polynomial (as shown below). It is best to have a program that can simplify it for you, such as Mathcad.
\( -1 \cdot x^3+51.8167 \cdot x^2-89.4833 \cdot x+33.2632=0 \)
Roots of the equation $$ \mathrm{x}_1=0.537 \quad \mathrm{x}_2=1.238 \quad \mathrm{x}_3=50.042 $$ since \( \mathrm{x}=\frac{1}{\sqrt{\mathrm{x}}} \cdot \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}} \)
Natural vibration frequencies
$$ \begin{aligned} &\omega_1=\frac{1}{\sqrt{x_3}}=0.14136 \cdot \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}} \\ &\omega_2=\frac{1}{\sqrt{x_2}}=0.899 \cdot \sqrt{\frac{EI}{\mathrm{m}}} \\ &\omega_3=\frac{1}{\sqrt{x_1}}=1.3647 \cdot \sqrt{\frac{EI}{\mathrm{m}}} \end{aligned} $$ Bending rigidity $$ \begin{aligned} &\text{For} \quad \mathrm{I}=2140 \cdot 10^{-8} \mathrm{~m}^4 \quad \text{and Young's modulus for steel} \quad \mathrm{E}=200 \cdot 10^9 \mathrm{~Pa} \\ &\mathrm{EI}=\mathrm{E} \cdot \mathrm{I}=4280000.000 \mathrm{Nm}^2 \quad \mathrm{~m}=100 \quad \mathrm{~kg} \\ &\omega_{1}=0.14136 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}=29.245 \quad \mathrm{rad/s} \\ &\omega_{2}=0.899 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}=185.939 \frac{\mathrm{rad}}{\mathrm{s}} \\ &\omega_{3}=1.365 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}=282.33 \quad \frac{\mathrm{rad}}{\mathrm{s}} \end{aligned} $$
Determining the shape of vibrations $$ \begin{aligned} &\left(\mathrm{m}_1 \cdot \delta_{11}-\mathrm{x}\right) \cdot \mathrm{A}_{11}+\mathrm{m}_2 \cdot \delta_{12} \cdot \mathrm{A}_{21}+\mathrm{m}_3 \cdot \delta_{13} \cdot \mathrm{A}_{31}=0 \\ &\mathrm{~m}_1 \cdot \delta_{12} \cdot \mathrm{A}_{11}+\left(\mathrm{m}_2 \cdot \delta_{22}-\mathrm{x}\right) \cdot \mathrm{A}_{21}+\mathrm{m}_3 \cdot \delta_{23} \cdot \mathrm{A}_{31}=0 \\ &\mathrm{~m}_1 \cdot \delta_{31} \cdot \mathrm{A}_{11}+\mathrm{m}_2 \cdot \delta_{32} \cdot \mathrm{A}_{21}+\left(\mathrm{m}_3 \cdot \delta_{33}-\mathrm{x}\right) \cdot \mathrm{A}_{31}=0 \end{aligned} $$
We solve such an equation three times, because once we substitute "x" with "x1", once with "x2", and once with "x3".
After substituting x, we have a system of 3 equations with three variables A11, A21, A31. This system of equations always has infinitely many solutions,
so we need to show one example solution. That means assuming one of the variables is equal to 1, and we will have a system of 3 equations with two variables left, which we can solve and compute the remaining two variables.
for \( \quad \mathrm{x}=\mathrm{x}_1=0.537 \quad assume \quad \mathrm{A}_{11}=1 \)
$$ \begin{aligned} &0.476+0.416 \cdot \mathrm{A}_{21}+4.825 \cdot \mathrm{A}_{31}=0 \\ &-0.416+0.442 \mathrm{~A}_{21}-1.7895 \cdot \mathrm{A}_{31}=0 \\ &1.9298-0.716 \cdot \mathrm{A}_{21}+49.288 \cdot \mathrm{A}_{31}=0 \end{aligned} $$ Solving the first two equations of the system
$$ \begin{aligned} &\mathrm{A}_{21}=0.831 \\ &\mathrm{~A}_{31}=-0.027 \end{aligned} $$ And the form of vibrations
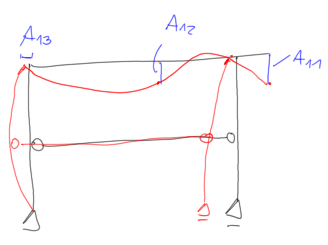
for \( \quad \mathrm{x}=\mathrm{x}_2=1.238 \quad assume \quad \mathrm{A}_{12}=1 \)
$$ \begin{aligned} &-0.225-0.416 \cdot \mathrm{A}_{22}+4.825 \cdot \mathrm{A}_{32}=0 \\ &-0.416+0.442 \cdot \mathrm{A}_{22}-1.7895 \cdot \mathrm{A}_{32}=0 \\ &1.9298-0.716 \cdot \mathrm{A}_{22}+49.288 \cdot \mathrm{A}_{32}=0 \end{aligned} $$ Solving the first two equations of the system
$$ \begin{aligned} &\mathrm{A}_{22}=0.536 \\ &\mathrm{~A}_{32}=-0.013 \end{aligned} $$ And the form of vibrations

for \( \quad \mathrm{x}=\mathrm{x}_3=50.042 \quad assume \quad \mathrm{A}_{13}=1 \)
$$ \begin{aligned} &-371.765-0.416 \cdot \mathrm{A}_{23}+4.825 \cdot \mathrm{A}_{33}=0 \\ &-0.416+0.442 \cdot \mathrm{A}_{23}-1.7895 \cdot \mathrm{A}_{33}=0 \\ &1.9298-0.716 \cdot \mathrm{A}_{23}+49.288 \cdot \mathrm{A}_{33}=0 \end{aligned} $$ Solving the first two equations of the system
$$ \begin{aligned} &\mathrm{A}_{23}=1.571 \\ &\mathrm{~A}_{33}=-0.043 \end{aligned} $$ And the form of vibrations

&-0.416-0.259 \cdot \mathrm{A}_{22}-1.7895 \cdot \mathrm{A}_{32}=0 \\ &1.9298-0.716 \cdot \mathrm{A}_{22}+48.587 \cdot \mathrm{A}_{32}=0 \end{aligned} $$ I solve the system of the first two equations
$$ \begin{aligned} &\mathrm{A}_{22}=-1.208 \\ &\mathrm{A}_{32}=-0.0575 \end{aligned} $$ Second form of vibrations
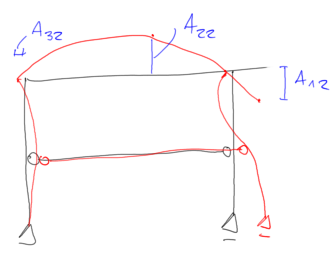
for \( \quad \mathrm{x}=\mathrm{x}_3=50.042 \quad I \quad assume \quad \mathrm{A}_{13}=1 \)
$$ \begin{gathered} -49.0286-0.416 \cdot \mathrm{A}_{23}+4.825 \cdot \mathrm{A}_{33}=0 \\ -0.416-49.063 \cdot \mathrm{A}_{23}-1.7895 \cdot \mathrm{A}_{33}=0 \\ 1.9298-0.716 \cdot \mathrm{A}_{23}-0.217 \cdot \mathrm{A}_{33}=0 \end{gathered} $$ I solve the system of the first two equations
$$ \begin{aligned} &\mathrm{A}_{23}=-0.378 \\ &\mathrm{A}_{33}=10.130 \end{aligned} $$ Third form of vibrations
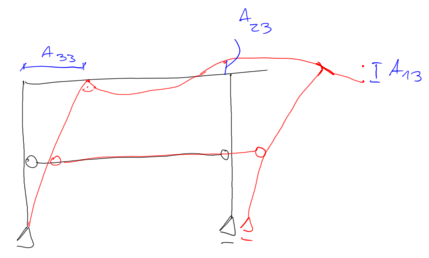
Checking the conditions of orthogonality
\begin{aligned} &\mathrm{m}_1 \cdot \mathrm{A}_{11} \cdot \mathrm{A}_{12}+\mathrm{m}_2 \cdot \mathrm{A}_{21} \cdot \mathrm{A}_{22}+\mathrm{m}_3 \cdot \mathrm{A}_{31} \cdot \mathrm{A}_{32}=0 \\ &\mathrm{~m}_1 \cdot \mathrm{A}_{12} \cdot \mathrm{A}_{13}+\mathrm{m}_2 \cdot \mathrm{A}_{22} \cdot \mathrm{A}_{23}+\mathrm{m}_3 \cdot \mathrm{A}_{32} \cdot \mathrm{A}_{33}=0 \\ &\mathrm{~m}_1 \cdot \mathrm{A}_{11} \cdot \mathrm{A}_{13}+\mathrm{m}_2 \cdot \mathrm{A}_{21} \cdot \mathrm{A}_{23}+\mathrm{m}_3 \cdot \mathrm{A}_{31} \cdot \mathrm{A}_{33}=0 \\ \end{aligned}
\begin{aligned} &1 \cdot 1 \cdot \mathrm{m}+1 \mathrm{~m} \cdot 0.831 \cdot(-1.208)+2.5 \mathrm{~m} \cdot(-0.027) \cdot(-0.0575) \rightarrow 0.00003 \mathrm{~m} \sim 0 \\ &1 \cdot 1 \cdot \mathrm{m}+1 \mathrm{~m} \cdot 0.831 \cdot(-1.208)+2.5 \mathrm{~m} \cdot(-0.027) \cdot(-0.0575) \rightarrow 0.00003 \mathrm{~m} \sim 0 \\ &1 \cdot 1 \cdot \mathrm{m}+1 \mathrm{~m} \cdot 0.831 \cdot(-0.378)+2.5 \mathrm{~m} \cdot(-0.027) \cdot 10.1297 \rightarrow 0.00213 \mathrm{~m} \sim 0 \end{aligned}
the check gives a positive result
r - reactions
p - hinges
a - closed circuits
\( \mathrm{SSD} = 3 - 3 - 2 + 3 \cdot 1 = 1 \)
Number of degrees of dynamic freedom
\( \mathrm{LSSD} = 3 \\ \quad \mathrm{~m}_1 = 100 \ kg \\ \quad \mathrm{~m}_2 = 100 \ kg \\ \quad \mathrm{~m}_3 = 250 \ kg
\)
assuming
\( \mathrm{m} = 100 \ kg \)
\( m_1 = m, \\ m_2 = m, \\ m_3 = 2.5m \)

We will solve the frame with the METHOD OF FORCES.
Basic system of the force method

Common unit state

Reactions
$$ \begin{aligned} &\Sigma \mathrm{M}_{\mathrm{A}} = 0 \quad 1 \cdot 2-1 \cdot 2-\mathrm{V}_{\mathrm{B}} \cdot 5 = 0 \quad \mathrm{~V}_{\mathrm{B}} = 0 \\ &\delta_{11} = \frac{1}{\mathrm{EI}} \cdot\left(\frac{1}{3} 2 \cdot 2 \cdot 2+2 \cdot 5 \cdot 2+\frac{1}{3} 2 \cdot 2 \cdot 2\right) = \frac{76}{3} \cdot \frac{1}{\mathrm{EI}} \end{aligned} $$ Now we do parallel analysis for all load cases, calculate the integration of δ1p separately for each case, calculate x1 (solving the canonical equation) and draw the final charts.

Dynamic deltas from the reduction theorem $$ \begin{aligned} &\delta_{11}=\int \frac{\mathrm{M}_{\mathrm{Ost} 1} \cdot \mathrm{M}_{\mathrm{P} 1}}{\mathrm{EI}} \mathrm{dS} \\ &\delta_{11}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{5}{6} \cdot\left(2 \cdot 1 \cdot \frac{23}{38}-1 \cdot \frac{15}{38}\right)+\frac{1}{3} \cdot 1 \cdot 1 \cdot 1\right]=\frac{77}{76} \cdot \frac{1}{\mathrm{EI}} \end{aligned} $$ $$ \begin{aligned} &\delta_{22}=\int \frac{\mathrm{M}_{\mathrm{Ost} 2} \cdot \mathrm{M}_{\mathrm{P} 2}}{\mathrm{EI}} \mathrm{dS} \\ &\delta_{22}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{3}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{69}{95}-1.2 \cdot \frac{9}{19}\right)+\frac{2}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{69}{95}-1.2 \cdot \frac{9}{19}\right)\right]=\frac{93}{95} \cdot \frac{1}{\mathrm{EI}} \end{aligned} $$ $$ \begin{aligned} &\delta_{33}=\int \frac{\mathrm{M}_{\mathrm{Ost} 3} \cdot \mathrm{M}_{\mathrm{P} 3}}{\mathrm{EI}} \mathrm{dS} \\ &\delta_{33}=\frac{1}{\mathrm{EI}} \cdot\left[\begin{array}{l} \frac{1}{3} \cdot 2 \cdot 2 \cdot 2+\frac{2}{6} \cdot\left(2 \cdot 2 \cdot 2+2 \cdot \frac{36}{19} \cdot 4+\frac{36}{19} \cdot 2+4 \cdot 2\right) \ldots \\ +\frac{5}{6} \cdot\left(2 \cdot 4 \cdot \frac{36}{19}-4 \cdot \frac{40}{19}\right) \end{array}\right]=\frac{1136}{57} \cdot \frac{1}{\mathrm{EI}} \end{aligned} $$ $$ \begin{aligned} &\delta_{12}=\int \frac{\mathrm{M}_{\mathrm{Ost} 1} \cdot \mathrm{M}_{\mathrm{P} 2}}{\mathrm{EI}} \mathrm{dS} \\ &\delta_{12}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{3}{6} \cdot\left(-2 \cdot 1.2 \cdot \frac{39}{190}+1.2 \cdot \frac{15}{38}\right)-\frac{2}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{39}{190}+1.2 \cdot \frac{23}{38}\right)\right]=-\frac{79}{190} \cdot \frac{1}{\mathrm{EI}} \quad \delta_{21}=\delta_{12} \end{aligned} $$ $$ \begin{aligned} &\delta_{13}=\int \frac{\mathrm{M}_{\mathrm{Ost} 3} \cdot \mathrm{M}_{\mathrm{P} 1}}{\mathrm{EI}} \mathrm{dS} \\ &\delta_{13}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{5}{6} \cdot\left(2 \cdot 1 \cdot \frac{40}{19}-1 \cdot \frac{36}{19}\right)\right]=\frac{110}{57} \cdot \frac{1}{\mathrm{EI}} \quad \delta_{31}=\delta_{13} \\ &\delta_{23}=\int \frac{\mathrm{M}_{\mathrm{Ost} 3} \cdot \mathrm{M}_{\mathrm{P} 2}}{\mathrm{EI}} \mathrm{dS} \\ &\delta_{23}=\frac{1}{\mathrm{EI}}\left[\frac{3}{6} \cdot\left(-2 \cdot 1.2 \cdot \frac{48}{95}+1 \cdot 2 \cdot \frac{36}{19}\right)-\frac{2}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{48}{95}+1.2 \cdot \frac{40}{19}\right)\right]=-\frac{68}{95} \cdot \frac{1}{\mathrm{EI}} \quad \delta_{32}=\delta_{23} \end{aligned} $$ assuming \( \mathrm{m}=100 \mathrm{~kg} \quad \mathrm{~m}_1=1 \mathrm{~m} \quad \mathrm{~m}_2=1 \mathrm{~m} \quad \mathrm{~m}_3=2.5 \mathrm{~m} \)
Finding the roots of the equation
$$ \left|\left(\begin{array}{ccc} \mathrm{m}_1 \cdot \delta_{11}-\frac{1}{\omega^2} & \mathrm{~m}_2 \cdot \delta_{12} & \mathrm{~m}_3 \cdot \delta_{13} \\ \mathrm{~m}_1 \cdot \delta_{21} & \mathrm{~m}_2 \cdot \delta_{22}-\frac{1}{\omega^2} & \mathrm{~m}_3 \cdot \delta_{23} \\ \mathrm{~m}_1 \cdot \delta_{31} & \mathrm{~m}_2 \cdot \delta_{32} & \mathrm{~m}_3 \cdot \delta_{33}-\frac{1}{\omega^2} \end{array}\right)\right|=0 $$ (multiply both sides by El/m ) substitute \( \quad \mathrm{x}=\frac{1}{\omega^2} \frac{\mathrm{EI}}{\mathrm{m}} \)\( \left[\begin{array}{ccc} 1 \cdot \frac{77}{76}-x & 1 \cdot\left(-\frac{79}{190}\right) & \frac{5}{2} \cdot \frac{110}{57} \\ 1 \cdot\left(-\frac{79}{190}\right) & 1 \cdot \frac{93}{95}-x & \frac{5}{2}\left(\frac{68}{95}\right) \\ 1 \cdot \frac{110}{57} & 1 \cdot\left(\frac{68}{95}\right) & \frac{5}{2} \cdot \frac{1136}{57}-x \end{array}\right]=0 \)
\( \left[\begin{array}{llc} \frac{77}{76}-\mathrm{x} & -\frac{79}{190} & \frac{275}{57} \\ -\frac{79}{190} & \frac{93}{95}-\mathrm{x} & -\frac{34}{19} \\ \frac{110}{57} & -\frac{68}{95} & \frac{2840}{57}-\mathrm{x} \end{array}\right]=0 \)
Then you need to use the Sarrus method to calculate the determinant of the above 3x3 matrix and simplify it to a 3rd degree polynomial (as shown below). It is best to have a program that can simplify it for you, such as Mathcad.
\( -1 \cdot x^3+51.8167 \cdot x^2-89.4833 \cdot x+33.2632=0 \)
Roots of the equation $$ \mathrm{x}_1=0.537 \quad \mathrm{x}_2=1.238 \quad \mathrm{x}_3=50.042 $$ since \( \mathrm{x}=\frac{1}{\sqrt{\mathrm{x}}} \cdot \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}} \)
Natural vibration frequencies
$$ \begin{aligned} &\omega_1=\frac{1}{\sqrt{x_3}}=0.14136 \cdot \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}} \\ &\omega_2=\frac{1}{\sqrt{x_2}}=0.899 \cdot \sqrt{\frac{EI}{\mathrm{m}}} \\ &\omega_3=\frac{1}{\sqrt{x_1}}=1.3647 \cdot \sqrt{\frac{EI}{\mathrm{m}}} \end{aligned} $$ Bending rigidity $$ \begin{aligned} &\text{For} \quad \mathrm{I}=2140 \cdot 10^{-8} \mathrm{~m}^4 \quad \text{and Young's modulus for steel} \quad \mathrm{E}=200 \cdot 10^9 \mathrm{~Pa} \\ &\mathrm{EI}=\mathrm{E} \cdot \mathrm{I}=4280000.000 \mathrm{Nm}^2 \quad \mathrm{~m}=100 \quad \mathrm{~kg} \\ &\omega_{1}=0.14136 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}=29.245 \quad \mathrm{rad/s} \\ &\omega_{2}=0.899 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}=185.939 \frac{\mathrm{rad}}{\mathrm{s}} \\ &\omega_{3}=1.365 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}=282.33 \quad \frac{\mathrm{rad}}{\mathrm{s}} \end{aligned} $$
Determining the shape of vibrations $$ \begin{aligned} &\left(\mathrm{m}_1 \cdot \delta_{11}-\mathrm{x}\right) \cdot \mathrm{A}_{11}+\mathrm{m}_2 \cdot \delta_{12} \cdot \mathrm{A}_{21}+\mathrm{m}_3 \cdot \delta_{13} \cdot \mathrm{A}_{31}=0 \\ &\mathrm{~m}_1 \cdot \delta_{12} \cdot \mathrm{A}_{11}+\left(\mathrm{m}_2 \cdot \delta_{22}-\mathrm{x}\right) \cdot \mathrm{A}_{21}+\mathrm{m}_3 \cdot \delta_{23} \cdot \mathrm{A}_{31}=0 \\ &\mathrm{~m}_1 \cdot \delta_{31} \cdot \mathrm{A}_{11}+\mathrm{m}_2 \cdot \delta_{32} \cdot \mathrm{A}_{21}+\left(\mathrm{m}_3 \cdot \delta_{33}-\mathrm{x}\right) \cdot \mathrm{A}_{31}=0 \end{aligned} $$
We solve such an equation three times, because once we substitute "x" with "x1", once with "x2", and once with "x3".
After substituting x, we have a system of 3 equations with three variables A11, A21, A31. This system of equations always has infinitely many solutions,
so we need to show one example solution. That means assuming one of the variables is equal to 1, and we will have a system of 3 equations with two variables left, which we can solve and compute the remaining two variables.
for \( \quad \mathrm{x}=\mathrm{x}_1=0.537 \quad assume \quad \mathrm{A}_{11}=1 \)
$$ \begin{aligned} &0.476+0.416 \cdot \mathrm{A}_{21}+4.825 \cdot \mathrm{A}_{31}=0 \\ &-0.416+0.442 \mathrm{~A}_{21}-1.7895 \cdot \mathrm{A}_{31}=0 \\ &1.9298-0.716 \cdot \mathrm{A}_{21}+49.288 \cdot \mathrm{A}_{31}=0 \end{aligned} $$ Solving the first two equations of the system
$$ \begin{aligned} &\mathrm{A}_{21}=0.831 \\ &\mathrm{~A}_{31}=-0.027 \end{aligned} $$ And the form of vibrations

for \( \quad \mathrm{x}=\mathrm{x}_2=1.238 \quad assume \quad \mathrm{A}_{12}=1 \)
$$ \begin{aligned} &-0.225-0.416 \cdot \mathrm{A}_{22}+4.825 \cdot \mathrm{A}_{32}=0 \\ &-0.416+0.442 \cdot \mathrm{A}_{22}-1.7895 \cdot \mathrm{A}_{32}=0 \\ &1.9298-0.716 \cdot \mathrm{A}_{22}+49.288 \cdot \mathrm{A}_{32}=0 \end{aligned} $$ Solving the first two equations of the system
$$ \begin{aligned} &\mathrm{A}_{22}=0.536 \\ &\mathrm{~A}_{32}=-0.013 \end{aligned} $$ And the form of vibrations

for \( \quad \mathrm{x}=\mathrm{x}_3=50.042 \quad assume \quad \mathrm{A}_{13}=1 \)
$$ \begin{aligned} &-371.765-0.416 \cdot \mathrm{A}_{23}+4.825 \cdot \mathrm{A}_{33}=0 \\ &-0.416+0.442 \cdot \mathrm{A}_{23}-1.7895 \cdot \mathrm{A}_{33}=0 \\ &1.9298-0.716 \cdot \mathrm{A}_{23}+49.288 \cdot \mathrm{A}_{33}=0 \end{aligned} $$ Solving the first two equations of the system
$$ \begin{aligned} &\mathrm{A}_{23}=1.571 \\ &\mathrm{~A}_{33}=-0.043 \end{aligned} $$ And the form of vibrations

&-0.416-0.259 \cdot \mathrm{A}_{22}-1.7895 \cdot \mathrm{A}_{32}=0 \\ &1.9298-0.716 \cdot \mathrm{A}_{22}+48.587 \cdot \mathrm{A}_{32}=0 \end{aligned} $$ I solve the system of the first two equations
$$ \begin{aligned} &\mathrm{A}_{22}=-1.208 \\ &\mathrm{A}_{32}=-0.0575 \end{aligned} $$ Second form of vibrations

for \( \quad \mathrm{x}=\mathrm{x}_3=50.042 \quad I \quad assume \quad \mathrm{A}_{13}=1 \)
$$ \begin{gathered} -49.0286-0.416 \cdot \mathrm{A}_{23}+4.825 \cdot \mathrm{A}_{33}=0 \\ -0.416-49.063 \cdot \mathrm{A}_{23}-1.7895 \cdot \mathrm{A}_{33}=0 \\ 1.9298-0.716 \cdot \mathrm{A}_{23}-0.217 \cdot \mathrm{A}_{33}=0 \end{gathered} $$ I solve the system of the first two equations
$$ \begin{aligned} &\mathrm{A}_{23}=-0.378 \\ &\mathrm{A}_{33}=10.130 \end{aligned} $$ Third form of vibrations

Checking the conditions of orthogonality
\begin{aligned} &\mathrm{m}_1 \cdot \mathrm{A}_{11} \cdot \mathrm{A}_{12}+\mathrm{m}_2 \cdot \mathrm{A}_{21} \cdot \mathrm{A}_{22}+\mathrm{m}_3 \cdot \mathrm{A}_{31} \cdot \mathrm{A}_{32}=0 \\ &\mathrm{~m}_1 \cdot \mathrm{A}_{12} \cdot \mathrm{A}_{13}+\mathrm{m}_2 \cdot \mathrm{A}_{22} \cdot \mathrm{A}_{23}+\mathrm{m}_3 \cdot \mathrm{A}_{32} \cdot \mathrm{A}_{33}=0 \\ &\mathrm{~m}_1 \cdot \mathrm{A}_{11} \cdot \mathrm{A}_{13}+\mathrm{m}_2 \cdot \mathrm{A}_{21} \cdot \mathrm{A}_{23}+\mathrm{m}_3 \cdot \mathrm{A}_{31} \cdot \mathrm{A}_{33}=0 \\ \end{aligned}
\begin{aligned} &1 \cdot 1 \cdot \mathrm{m}+1 \mathrm{~m} \cdot 0.831 \cdot(-1.208)+2.5 \mathrm{~m} \cdot(-0.027) \cdot(-0.0575) \rightarrow 0.00003 \mathrm{~m} \sim 0 \\ &1 \cdot 1 \cdot \mathrm{m}+1 \mathrm{~m} \cdot 0.831 \cdot(-1.208)+2.5 \mathrm{~m} \cdot(-0.027) \cdot(-0.0575) \rightarrow 0.00003 \mathrm{~m} \sim 0 \\ &1 \cdot 1 \cdot \mathrm{m}+1 \mathrm{~m} \cdot 0.831 \cdot(-0.378)+2.5 \mathrm{~m} \cdot(-0.027) \cdot 10.1297 \rightarrow 0.00213 \mathrm{~m} \sim 0 \end{aligned}
the check gives a positive result
If you have any questions, comments, or think you have found a mistake in this solution, please send us a message at kontakt@edupanda.pl.
