Solución
Grado de indeterminación estática
$$
\mathrm{SSN}=\mathrm{r}-3-\mathrm{p}+3 \cdot \mathrm{a}
$$
donde:
r - reacciones
p - articulaciones
a - circuitos cerrados
\(
\mathrm{SSN}=3-3-2+3 \cdot 1=1
\)
Número de grados de libertad dinámica
\(
\mathrm{LSSD}=3 \\
\quad \mathrm{~m}_1=100 \ kg \\
\quad \mathrm{m}_2=100\ kg \\
\quad \mathrm{m}_3=250\ kg \\
\)
asumiendo
\( \mathrm{m}=100 \mathrm{~kg} \) \\
\( m_1=m, \\ m_2=m, \\ m_3=2.5m \) \\
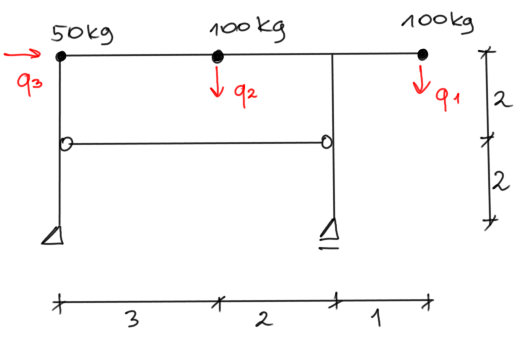 Resolveremos el marco por el método de las fuerzas.
Sistema base del método de las fuerzas
Resolveremos el marco por el método de las fuerzas.
Sistema base del método de las fuerzas
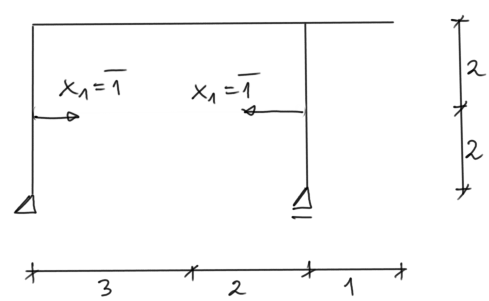 Estado unitario común
Estado unitario común
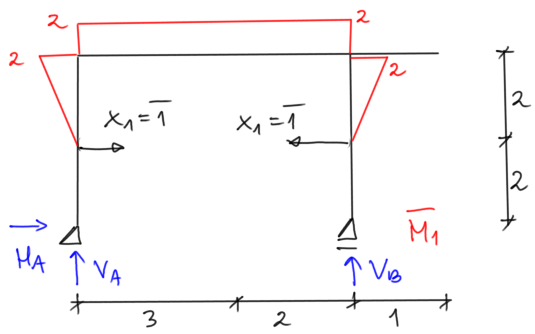 Reacciones
$$
\begin{aligned}
&\Sigma \mathrm{M}_{\mathrm{A}}=0 \quad 1 \cdot 2-1 \cdot 2-\mathrm{V}_{\mathrm{B}} \cdot 5=0 \quad \mathrm{~V}_{\mathrm{B}}=0 \\
&\delta_{11}=\frac{1}{\mathrm{EI}} \cdot\left(\frac{1}{3} 2 \cdot 2 \cdot 2+2 \cdot 5 \cdot 2+\frac{1}{3} 2 \cdot 2 \cdot 2\right)=\frac{76}{3} \cdot \frac{1}{\mathrm{EI}}
\end{aligned}
$$
Ahora hacemos el estado P para cada caso de carga, calculamos la integración por separado para cada caso, resolvemos la ecuación canónica y trazamos los gráficos finales.
Reacciones
$$
\begin{aligned}
&\Sigma \mathrm{M}_{\mathrm{A}}=0 \quad 1 \cdot 2-1 \cdot 2-\mathrm{V}_{\mathrm{B}} \cdot 5=0 \quad \mathrm{~V}_{\mathrm{B}}=0 \\
&\delta_{11}=\frac{1}{\mathrm{EI}} \cdot\left(\frac{1}{3} 2 \cdot 2 \cdot 2+2 \cdot 5 \cdot 2+\frac{1}{3} 2 \cdot 2 \cdot 2\right)=\frac{76}{3} \cdot \frac{1}{\mathrm{EI}}
\end{aligned}
$$
Ahora hacemos el estado P para cada caso de carga, calculamos la integración por separado para cada caso, resolvemos la ecuación canónica y trazamos los gráficos finales.
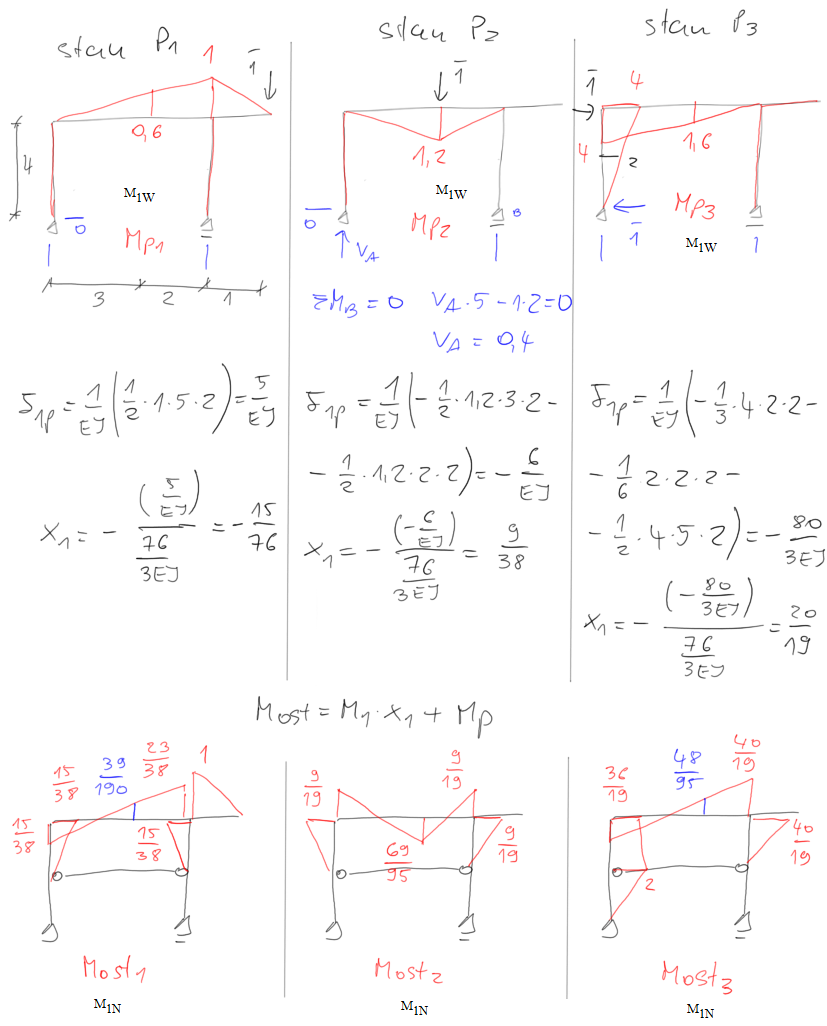 Deltas dinámicas del teorema de reducción
$$
\begin{aligned}
&\delta_{11}=\int \frac{\mathrm{M}_{\mathrm{Ost} 1} \cdot \mathrm{M}_{\mathrm{P} 1}}{\mathrm{EI}} \mathrm{dS} \\
&\delta_{11}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{5}{6} \cdot\left(2 \cdot 1 \cdot \frac{23}{38}-1 \cdot \frac{15}{38}\right)+\frac{1}{3} \cdot 1 \cdot 1 \cdot 1\right]=\frac{77}{76} \cdot \frac{1}{\mathrm{EI}}
\end{aligned}
$$
$$
\begin{aligned}
&\delta_{22}=\int \frac{\mathrm{M}_{\mathrm{ost} 2} \cdot \mathrm{M}_{\mathrm{P} 2}}{\mathrm{EI}} \mathrm{dS} \\
&\delta_{22}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{3}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{69}{95}-1.2 \cdot \frac{9}{19}\right)+\frac{2}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{69}{95}-1.2 \cdot \frac{9}{19}\right)\right]=\frac{93}{95} \cdot \frac{1}{\mathrm{EI}}
\end{aligned}
$$
$$
\begin{aligned}
&\delta_{33}=\int \frac{\mathrm{M}_{\mathrm{ost} 3} \cdot \mathrm{M}_{\mathrm{P} 3}}{\mathrm{EI}} \mathrm{dS} \\
&\delta_{33}=\frac{1}{\mathrm{EI}} \cdot\left[\begin{array}{l}
\frac{1}{3} \cdot 2 \cdot 2 \cdot 2+\frac{2}{6} \cdot\left(2 \cdot 2 \cdot 2+2 \cdot \frac{36}{19} \cdot 4+\frac{36}{19} \cdot 2+4 \cdot 2\right) \ldots \\
+\frac{5}{6} \cdot\left(2 \cdot 4 \cdot \frac{36}{19}-4 \cdot \frac{40}{19}\right)
\end{array}\right]=\frac{1136}{57} \cdot \frac{1}{\mathrm{EI}}
\end{aligned}
$$
$$
\begin{aligned}
&\delta_{12}=\int \frac{\mathrm{M}_{\mathrm{ost} 1} \cdot \mathrm{M}_{\mathrm{P} 2}}{\mathrm{EI}} \mathrm{dS} \\
&\delta_{12}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{3}{6} \cdot\left(-2 \cdot 1.2 \cdot \frac{39}{190}+1.2 \cdot \frac{15}{38}\right)-\frac{2}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{39}{190}+1.2 \cdot \frac{23}{38}\right)\right]=-\frac{79}{190} \cdot \frac{1}{\mathrm{EI}} \quad \delta_{21}=\delta_{12}
\end{aligned}
$$
$$
\begin{aligned}
&\delta_{13}=\int \frac{\mathrm{M}_{\mathrm{ost} 3} \cdot \mathrm{M}_{\mathrm{P} 1}}{\mathrm{EI}} \mathrm{dS} \\
&\delta_{13}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{5}{6} \cdot\left(2 \cdot 1 \cdot \frac{40}{19}-1 \cdot \frac{36}{19}\right)\right]=\frac{110}{57} \cdot \frac{1}{\mathrm{EI}} \quad \delta_{31}=\delta_{13} \\
&\delta_{23}=\int \frac{\mathrm{M}_{\mathrm{Ost} 3} \cdot \mathrm{M}_{\mathrm{P} 2}}{\mathrm{EI}} \mathrm{dS} \\
&\delta_{23}=\frac{1}{\mathrm{EI}}\left[\frac{3}{6} \cdot\left(-2 \cdot 1.2 \cdot \frac{48}{95}+1 \cdot 2 \cdot \frac{36}{19}\right)-\frac{2}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{48}{95}+1.2 \cdot \frac{40}{19}\right)\right]=-\frac{68}{95} \cdot \frac{1}{\mathrm{EI}} \quad \delta_{32}=\delta_{23}
\end{aligned}
$$
asumiendo \( \mathrm{m}=100 \mathrm{~kg} \quad \mathrm{~m}_1=1 \mathrm{~m} \quad \mathrm{~m}_2=1 \mathrm{~m} \quad \mathrm{~m}_3=2.5 \mathrm{~m} \)
Deltas dinámicas del teorema de reducción
$$
\begin{aligned}
&\delta_{11}=\int \frac{\mathrm{M}_{\mathrm{Ost} 1} \cdot \mathrm{M}_{\mathrm{P} 1}}{\mathrm{EI}} \mathrm{dS} \\
&\delta_{11}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{5}{6} \cdot\left(2 \cdot 1 \cdot \frac{23}{38}-1 \cdot \frac{15}{38}\right)+\frac{1}{3} \cdot 1 \cdot 1 \cdot 1\right]=\frac{77}{76} \cdot \frac{1}{\mathrm{EI}}
\end{aligned}
$$
$$
\begin{aligned}
&\delta_{22}=\int \frac{\mathrm{M}_{\mathrm{ost} 2} \cdot \mathrm{M}_{\mathrm{P} 2}}{\mathrm{EI}} \mathrm{dS} \\
&\delta_{22}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{3}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{69}{95}-1.2 \cdot \frac{9}{19}\right)+\frac{2}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{69}{95}-1.2 \cdot \frac{9}{19}\right)\right]=\frac{93}{95} \cdot \frac{1}{\mathrm{EI}}
\end{aligned}
$$
$$
\begin{aligned}
&\delta_{33}=\int \frac{\mathrm{M}_{\mathrm{ost} 3} \cdot \mathrm{M}_{\mathrm{P} 3}}{\mathrm{EI}} \mathrm{dS} \\
&\delta_{33}=\frac{1}{\mathrm{EI}} \cdot\left[\begin{array}{l}
\frac{1}{3} \cdot 2 \cdot 2 \cdot 2+\frac{2}{6} \cdot\left(2 \cdot 2 \cdot 2+2 \cdot \frac{36}{19} \cdot 4+\frac{36}{19} \cdot 2+4 \cdot 2\right) \ldots \\
+\frac{5}{6} \cdot\left(2 \cdot 4 \cdot \frac{36}{19}-4 \cdot \frac{40}{19}\right)
\end{array}\right]=\frac{1136}{57} \cdot \frac{1}{\mathrm{EI}}
\end{aligned}
$$
$$
\begin{aligned}
&\delta_{12}=\int \frac{\mathrm{M}_{\mathrm{ost} 1} \cdot \mathrm{M}_{\mathrm{P} 2}}{\mathrm{EI}} \mathrm{dS} \\
&\delta_{12}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{3}{6} \cdot\left(-2 \cdot 1.2 \cdot \frac{39}{190}+1.2 \cdot \frac{15}{38}\right)-\frac{2}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{39}{190}+1.2 \cdot \frac{23}{38}\right)\right]=-\frac{79}{190} \cdot \frac{1}{\mathrm{EI}} \quad \delta_{21}=\delta_{12}
\end{aligned}
$$
$$
\begin{aligned}
&\delta_{13}=\int \frac{\mathrm{M}_{\mathrm{ost} 3} \cdot \mathrm{M}_{\mathrm{P} 1}}{\mathrm{EI}} \mathrm{dS} \\
&\delta_{13}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{5}{6} \cdot\left(2 \cdot 1 \cdot \frac{40}{19}-1 \cdot \frac{36}{19}\right)\right]=\frac{110}{57} \cdot \frac{1}{\mathrm{EI}} \quad \delta_{31}=\delta_{13} \\
&\delta_{23}=\int \frac{\mathrm{M}_{\mathrm{Ost} 3} \cdot \mathrm{M}_{\mathrm{P} 2}}{\mathrm{EI}} \mathrm{dS} \\
&\delta_{23}=\frac{1}{\mathrm{EI}}\left[\frac{3}{6} \cdot\left(-2 \cdot 1.2 \cdot \frac{48}{95}+1 \cdot 2 \cdot \frac{36}{19}\right)-\frac{2}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{48}{95}+1.2 \cdot \frac{40}{19}\right)\right]=-\frac{68}{95} \cdot \frac{1}{\mathrm{EI}} \quad \delta_{32}=\delta_{23}
\end{aligned}
$$
asumiendo \( \mathrm{m}=100 \mathrm{~kg} \quad \mathrm{~m}_1=1 \mathrm{~m} \quad \mathrm{~m}_2=1 \mathrm{~m} \quad \mathrm{~m}_3=2.5 \mathrm{~m} \)
\( \left[\begin{array}{ccc} 1 \cdot \frac{77}{76}-x & 1 \cdot\left(-\frac{79}{190}\right) & \frac{5}{2} \cdot \frac{110}{57} \\ 1 \cdot\left(-\frac{79}{190}\right) & 1 \cdot \frac{93}{95}-x & \frac{5}{2}\left(\frac{68}{95}\right) \\ 1 \cdot \frac{110}{57} & 1 \cdot\left(\frac{68}{95}\right) & \frac{5}{2} \cdot \frac{1136}{57}-x \end{array}\right]=0 \)
\( \left[\begin{array}{llc} \frac{77}{76}-\mathrm{x} & -\frac{79}{190} & \frac{275}{57} \\ -\frac{79}{190} & \frac{93}{95}-\mathrm{x} & -\frac{34}{19} \\ \frac{110}{57} & -\frac{68}{95} & \frac{2840}{57}-\mathrm{x} \end{array}\right]=0 \)
A continuación, usando el método de Sarrus calculamos el determinante de la matriz 3x3 anterior y lo simplificamos a una forma polinómica de grado 3 (como se muestra a continuación). Sería mejor si tuviéramos un programa que pueda simplificar esto por nosotros, como Mathcad.
\( -1 \cdot x^3+51.8167 \cdot x^2-89.4833 \cdot x+33.2632=0 \)
Raíces de la ecuación $$ \mathrm{x}_1=0.537 \quad \mathrm{x}_2=1.238 \quad \mathrm{x}_3=50.042 $$ ya que \( \mathrm{x}=\frac{1}{\omega^2} \frac{\text { EI }}{\mathrm{m}} \quad \omega=\frac{1}{\sqrt{\mathrm{x}}} \cdot \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}} \)
Frecuencias propias de vibración $$ \begin{aligned} &\omega_1=\frac{1}{\sqrt{x_3}}=0.14136 \cdot \sqrt{\frac{\text { EI }}{\mathrm{m}}} \\ &\omega_2=\frac{1}{\sqrt{x_2}}=0.899 \cdot \sqrt{\frac{E I}{\mathrm{~m}}} \\ &\omega_3=\frac{1}{\sqrt{x_1}}=1.3647 \cdot \sqrt{\frac{E I}{\mathrm{~m}}} \end{aligned} $$ Rigidez a la flexión $$ \begin{aligned} &\text { Para } \quad \mathrm{I}=2140 \cdot 10^{-8} \mathrm{~m}^4 \quad \text { y el módulo de Young para el acero } \quad \mathrm{E}=200 \cdot 10^9 \mathrm{~Pa} \\ &\mathrm{EI}=\mathrm{E} \cdot \mathrm{I}=4280000.000 \mathrm{Nm}^2 \quad \mathrm{~m}=100 \quad \mathrm{~kg} \\ &\omega_{1}=0.14136 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}=29.245 \quad \frac{\mathrm{rad}}{\mathrm{s}} \\ &\omega_{2}=0.899 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}=185.939 \frac{\mathrm{rad}}{\mathrm{s}} \\ &\omega_{3}=1.365 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}=282.33 \quad \frac{\mathrm{rad}}{\mathrm{s}} \end{aligned} $$
Determinación de la forma de vibración $$ \begin{aligned} &\left(\mathrm{m}_1 \cdot \delta_{11}-\mathrm{x}\right) \cdot \mathrm{A}_{11}+\mathrm{m}_2 \cdot \delta_{12} \cdot \mathrm{A}_{21}+\mathrm{m}_3 \cdot \delta_{13} \cdot \mathrm{A}_{31}=0 \\ &\mathrm{~m}_1 \cdot \delta_{12} \cdot \mathrm{A}_{11}+\left(\mathrm{m}_2 \cdot \delta_{22}-\mathrm{x}\right) \cdot \mathrm{A}_{21}+\mathrm{m}_3 \cdot \delta_{23} \cdot \mathrm{A}_{31}=0 \\ &\mathrm{~m}_1 \cdot \delta_{31} \cdot \mathrm{A}_{11}+\mathrm{m}_2 \cdot \delta_{32} \cdot \mathrm{A}_{21}+\left(\mathrm{m}_3 \cdot \delta_{33}-\mathrm{x}\right) \cdot \mathrm{A}_{31}=0 \end{aligned} $$
Resolvemos el sistema de ecuaciones anterior tres veces, una vez para "x" igual a "x1", otra para "x2" y otra para "x3".
Sustituyendo x, tenemos un sistema de 3 ecuaciones con tres incógnitas A11, A21, A31. Este sistema de ecuaciones siempre tiene infinitas soluciones, por lo que debemos mostrar una solución de ejemplo. Es decir, asumimos un valor de una de las incógnitas igual a 1, y luego nos quedamos con un sistema de tres ecuaciones con dos incógnitas restantes, donde si resolvemos las dos primeras ecuaciones, podemos calcular las otras dos incógnitas restantes.
para \( \quad \mathrm{x}=\mathrm{x}_1=0.537 \quad asumo \quad \mathrm{A}_{11}=1 \)
$$ \begin{aligned} &0.476+0.416 \mathrm{~A}_{21}+4.825 \cdot \mathrm{A}_{31}=0 \\ &-0.416+0.442 \mathrm{~A}_{21}-1.7895 \cdot \mathrm{A}_{31}=0 \\ &1.9298-0.716 \cdot \mathrm{A}_{21}+49.288 \cdot \mathrm{A}_{31}=0 \end{aligned} $$ Resuelvo el sistema de las dos primeras ecuaciones
$$ \begin{aligned} &\mathrm{A}_{21}=0.831 \\ &\mathrm{~A}_{31}=-0.027 \end{aligned} $$ Y la forma de vibración sería
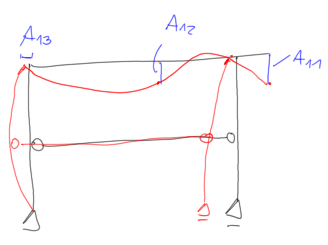 para \( \quad \mathrm{x}=\mathrm{x}_2=1.238 \quad asumo \quad \mathrm{A}_{12}=1 \)
para \( \quad \mathrm{x}=\mathrm{x}_2=1.238 \quad asumo \quad \mathrm{A}_{12}=1 \)
$$ \begin{aligned} &-0.225-0.416 \cdot \mathrm{A}_{22}+4.825 \cdot \mathrm{A}_{32}=0 \\ &-0.416+0.442 \mathrm{~A}_{22}-1.7895 \cdot \mathrm{A}_{32}=0 \\ &1.9298-0.716 \cdot \mathrm{A}_{22}+49.288 \cdot \mathrm{A}_{32}=0 \end{aligned} $$ Resuelvo el sistema de las dos primeras ecuaciones
$$ \begin{aligned} &\mathrm{A}_{22}=0.905 \\ &\mathrm{~A}_{32}=-0.029 \end{aligned} $$ Y la forma de vibración sería &-0.416-0.259 \cdot \mathrm{A}_{22}-1.7895 \cdot \mathrm{A}_{32}=0 \\ &1.9298-0.716 \cdot \mathrm{A}_{22}+48.587 \cdot \mathrm{A}_{32}=0 \end{aligned} $$ We solve the system of the first two equations:
$$ \begin{aligned} &\mathrm{A}_{22}=-1.208 \\ &\mathrm{A}_{32}=-0.0575 \end{aligned} $$ Second form of vibration:
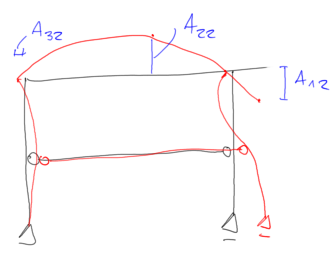
for \( \quad \mathrm{x}=\mathrm{x}_3=50.042 \quad I \quad assume \quad \mathrm{A}_{13}=1 \)
$$ \begin{gathered} -49.0286-0.416 \cdot \mathrm{A}_{23}+4.825 \cdot \mathrm{A}_{33}=0 \\ -0.416-49.063 \cdot \mathrm{A}_{23}-1.7895 \cdot \mathrm{A}_{33}=0 \\ 1.9298-0.716 \cdot \mathrm{A}_{23}-0.217 \cdot \mathrm{A}_{33}=0 \end{gathered} $$ We solve the system of the first two equations:
$$ \begin{aligned} &\mathrm{A}_{23}=-0.378 \\ &\mathrm{A}_{33}=10.130 \end{aligned} $$ Third form of vibration:
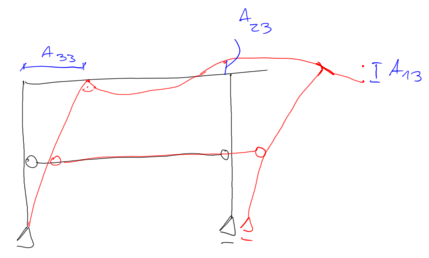
Checking the orthogonality conditions:
\begin{aligned} &\mathrm{m}_1 \cdot \mathrm{A}_{11} \cdot \mathrm{A}_{12}+\mathrm{m}_2 \cdot \mathrm{A}_{21} \cdot \mathrm{A}_{22}+\mathrm{m}_3 \cdot \mathrm{A}_{31} \cdot \mathrm{A}_{32}=0 \\ &\mathrm{~m}_1 \cdot \mathrm{A}_{12} \cdot \mathrm{A}_{13}+\mathrm{m}_2 \cdot \mathrm{A}_{22} \cdot \mathrm{A}_{23}+\mathrm{m}_3 \cdot \mathrm{A}_{32} \cdot \mathrm{A}_{33}=0 \\ &\mathrm{~m}_1 \cdot \mathrm{A}_{11} \cdot \mathrm{A}_{13}+\mathrm{m}_2 \cdot \mathrm{A}_{21} \cdot \mathrm{A}_{23}+\mathrm{m}_3 \cdot \mathrm{A}_{31} \cdot \mathrm{A}_{33}=0 \\ \end{aligned}
\begin{aligned} &1 \cdot 1 \cdot \mathrm{m}+1 \mathrm{~m} \cdot 0.831 \cdot(-1.208)+2.5 \mathrm{~m} \cdot(-0.027) \cdot(-0.0575) \rightarrow 0.00003 \mathrm{~m} \sim 0 \\ &1 \cdot 1 \cdot \mathrm{m}+1 \mathrm{~m} \cdot 0.831 \cdot(-1.208)+2.5 \mathrm{~m} \cdot(-0.027) \cdot(-0.0575) \rightarrow 0.00003 \mathrm{~m} \sim 0 \\ &1 \cdot 1 \cdot \mathrm{m}+1 \mathrm{~m} \cdot 0.831 \cdot(-0.378)+2.5 \mathrm{~m} \cdot(-0.027) \cdot 10.1297 \rightarrow 0.00213 \mathrm{~m} \sim 0 \end{aligned}
the check gives a positive result
 Resolveremos el marco por el método de las fuerzas.
Sistema base del método de las fuerzas
Resolveremos el marco por el método de las fuerzas.
Sistema base del método de las fuerzas
 Estado unitario común
Estado unitario común
 Reacciones
$$
\begin{aligned}
&\Sigma \mathrm{M}_{\mathrm{A}}=0 \quad 1 \cdot 2-1 \cdot 2-\mathrm{V}_{\mathrm{B}} \cdot 5=0 \quad \mathrm{~V}_{\mathrm{B}}=0 \\
&\delta_{11}=\frac{1}{\mathrm{EI}} \cdot\left(\frac{1}{3} 2 \cdot 2 \cdot 2+2 \cdot 5 \cdot 2+\frac{1}{3} 2 \cdot 2 \cdot 2\right)=\frac{76}{3} \cdot \frac{1}{\mathrm{EI}}
\end{aligned}
$$
Ahora hacemos el estado P para cada caso de carga, calculamos la integración por separado para cada caso, resolvemos la ecuación canónica y trazamos los gráficos finales.
Reacciones
$$
\begin{aligned}
&\Sigma \mathrm{M}_{\mathrm{A}}=0 \quad 1 \cdot 2-1 \cdot 2-\mathrm{V}_{\mathrm{B}} \cdot 5=0 \quad \mathrm{~V}_{\mathrm{B}}=0 \\
&\delta_{11}=\frac{1}{\mathrm{EI}} \cdot\left(\frac{1}{3} 2 \cdot 2 \cdot 2+2 \cdot 5 \cdot 2+\frac{1}{3} 2 \cdot 2 \cdot 2\right)=\frac{76}{3} \cdot \frac{1}{\mathrm{EI}}
\end{aligned}
$$
Ahora hacemos el estado P para cada caso de carga, calculamos la integración por separado para cada caso, resolvemos la ecuación canónica y trazamos los gráficos finales.
 Deltas dinámicas del teorema de reducción
$$
\begin{aligned}
&\delta_{11}=\int \frac{\mathrm{M}_{\mathrm{Ost} 1} \cdot \mathrm{M}_{\mathrm{P} 1}}{\mathrm{EI}} \mathrm{dS} \\
&\delta_{11}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{5}{6} \cdot\left(2 \cdot 1 \cdot \frac{23}{38}-1 \cdot \frac{15}{38}\right)+\frac{1}{3} \cdot 1 \cdot 1 \cdot 1\right]=\frac{77}{76} \cdot \frac{1}{\mathrm{EI}}
\end{aligned}
$$
$$
\begin{aligned}
&\delta_{22}=\int \frac{\mathrm{M}_{\mathrm{ost} 2} \cdot \mathrm{M}_{\mathrm{P} 2}}{\mathrm{EI}} \mathrm{dS} \\
&\delta_{22}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{3}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{69}{95}-1.2 \cdot \frac{9}{19}\right)+\frac{2}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{69}{95}-1.2 \cdot \frac{9}{19}\right)\right]=\frac{93}{95} \cdot \frac{1}{\mathrm{EI}}
\end{aligned}
$$
$$
\begin{aligned}
&\delta_{33}=\int \frac{\mathrm{M}_{\mathrm{ost} 3} \cdot \mathrm{M}_{\mathrm{P} 3}}{\mathrm{EI}} \mathrm{dS} \\
&\delta_{33}=\frac{1}{\mathrm{EI}} \cdot\left[\begin{array}{l}
\frac{1}{3} \cdot 2 \cdot 2 \cdot 2+\frac{2}{6} \cdot\left(2 \cdot 2 \cdot 2+2 \cdot \frac{36}{19} \cdot 4+\frac{36}{19} \cdot 2+4 \cdot 2\right) \ldots \\
+\frac{5}{6} \cdot\left(2 \cdot 4 \cdot \frac{36}{19}-4 \cdot \frac{40}{19}\right)
\end{array}\right]=\frac{1136}{57} \cdot \frac{1}{\mathrm{EI}}
\end{aligned}
$$
$$
\begin{aligned}
&\delta_{12}=\int \frac{\mathrm{M}_{\mathrm{ost} 1} \cdot \mathrm{M}_{\mathrm{P} 2}}{\mathrm{EI}} \mathrm{dS} \\
&\delta_{12}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{3}{6} \cdot\left(-2 \cdot 1.2 \cdot \frac{39}{190}+1.2 \cdot \frac{15}{38}\right)-\frac{2}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{39}{190}+1.2 \cdot \frac{23}{38}\right)\right]=-\frac{79}{190} \cdot \frac{1}{\mathrm{EI}} \quad \delta_{21}=\delta_{12}
\end{aligned}
$$
$$
\begin{aligned}
&\delta_{13}=\int \frac{\mathrm{M}_{\mathrm{ost} 3} \cdot \mathrm{M}_{\mathrm{P} 1}}{\mathrm{EI}} \mathrm{dS} \\
&\delta_{13}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{5}{6} \cdot\left(2 \cdot 1 \cdot \frac{40}{19}-1 \cdot \frac{36}{19}\right)\right]=\frac{110}{57} \cdot \frac{1}{\mathrm{EI}} \quad \delta_{31}=\delta_{13} \\
&\delta_{23}=\int \frac{\mathrm{M}_{\mathrm{Ost} 3} \cdot \mathrm{M}_{\mathrm{P} 2}}{\mathrm{EI}} \mathrm{dS} \\
&\delta_{23}=\frac{1}{\mathrm{EI}}\left[\frac{3}{6} \cdot\left(-2 \cdot 1.2 \cdot \frac{48}{95}+1 \cdot 2 \cdot \frac{36}{19}\right)-\frac{2}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{48}{95}+1.2 \cdot \frac{40}{19}\right)\right]=-\frac{68}{95} \cdot \frac{1}{\mathrm{EI}} \quad \delta_{32}=\delta_{23}
\end{aligned}
$$
asumiendo \( \mathrm{m}=100 \mathrm{~kg} \quad \mathrm{~m}_1=1 \mathrm{~m} \quad \mathrm{~m}_2=1 \mathrm{~m} \quad \mathrm{~m}_3=2.5 \mathrm{~m} \)
Deltas dinámicas del teorema de reducción
$$
\begin{aligned}
&\delta_{11}=\int \frac{\mathrm{M}_{\mathrm{Ost} 1} \cdot \mathrm{M}_{\mathrm{P} 1}}{\mathrm{EI}} \mathrm{dS} \\
&\delta_{11}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{5}{6} \cdot\left(2 \cdot 1 \cdot \frac{23}{38}-1 \cdot \frac{15}{38}\right)+\frac{1}{3} \cdot 1 \cdot 1 \cdot 1\right]=\frac{77}{76} \cdot \frac{1}{\mathrm{EI}}
\end{aligned}
$$
$$
\begin{aligned}
&\delta_{22}=\int \frac{\mathrm{M}_{\mathrm{ost} 2} \cdot \mathrm{M}_{\mathrm{P} 2}}{\mathrm{EI}} \mathrm{dS} \\
&\delta_{22}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{3}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{69}{95}-1.2 \cdot \frac{9}{19}\right)+\frac{2}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{69}{95}-1.2 \cdot \frac{9}{19}\right)\right]=\frac{93}{95} \cdot \frac{1}{\mathrm{EI}}
\end{aligned}
$$
$$
\begin{aligned}
&\delta_{33}=\int \frac{\mathrm{M}_{\mathrm{ost} 3} \cdot \mathrm{M}_{\mathrm{P} 3}}{\mathrm{EI}} \mathrm{dS} \\
&\delta_{33}=\frac{1}{\mathrm{EI}} \cdot\left[\begin{array}{l}
\frac{1}{3} \cdot 2 \cdot 2 \cdot 2+\frac{2}{6} \cdot\left(2 \cdot 2 \cdot 2+2 \cdot \frac{36}{19} \cdot 4+\frac{36}{19} \cdot 2+4 \cdot 2\right) \ldots \\
+\frac{5}{6} \cdot\left(2 \cdot 4 \cdot \frac{36}{19}-4 \cdot \frac{40}{19}\right)
\end{array}\right]=\frac{1136}{57} \cdot \frac{1}{\mathrm{EI}}
\end{aligned}
$$
$$
\begin{aligned}
&\delta_{12}=\int \frac{\mathrm{M}_{\mathrm{ost} 1} \cdot \mathrm{M}_{\mathrm{P} 2}}{\mathrm{EI}} \mathrm{dS} \\
&\delta_{12}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{3}{6} \cdot\left(-2 \cdot 1.2 \cdot \frac{39}{190}+1.2 \cdot \frac{15}{38}\right)-\frac{2}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{39}{190}+1.2 \cdot \frac{23}{38}\right)\right]=-\frac{79}{190} \cdot \frac{1}{\mathrm{EI}} \quad \delta_{21}=\delta_{12}
\end{aligned}
$$
$$
\begin{aligned}
&\delta_{13}=\int \frac{\mathrm{M}_{\mathrm{ost} 3} \cdot \mathrm{M}_{\mathrm{P} 1}}{\mathrm{EI}} \mathrm{dS} \\
&\delta_{13}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{5}{6} \cdot\left(2 \cdot 1 \cdot \frac{40}{19}-1 \cdot \frac{36}{19}\right)\right]=\frac{110}{57} \cdot \frac{1}{\mathrm{EI}} \quad \delta_{31}=\delta_{13} \\
&\delta_{23}=\int \frac{\mathrm{M}_{\mathrm{Ost} 3} \cdot \mathrm{M}_{\mathrm{P} 2}}{\mathrm{EI}} \mathrm{dS} \\
&\delta_{23}=\frac{1}{\mathrm{EI}}\left[\frac{3}{6} \cdot\left(-2 \cdot 1.2 \cdot \frac{48}{95}+1 \cdot 2 \cdot \frac{36}{19}\right)-\frac{2}{6} \cdot\left(2 \cdot 1.2 \cdot \frac{48}{95}+1.2 \cdot \frac{40}{19}\right)\right]=-\frac{68}{95} \cdot \frac{1}{\mathrm{EI}} \quad \delta_{32}=\delta_{23}
\end{aligned}
$$
asumiendo \( \mathrm{m}=100 \mathrm{~kg} \quad \mathrm{~m}_1=1 \mathrm{~m} \quad \mathrm{~m}_2=1 \mathrm{~m} \quad \mathrm{~m}_3=2.5 \mathrm{~m} \)
Encontrando las raíces de la ecuación
$$ \left|\left(\begin{array}{ccc} \mathrm{m}_1 \cdot \delta_{11}-\frac{1}{\omega^2} & \mathrm{~m}_2 \cdot \delta_{12} & \mathrm{~m}_3 \cdot \delta_{13} \\ \mathrm{~m}_1 \cdot \delta_{21} & \mathrm{~m}_2 \cdot \delta_{22}-\frac{1}{\omega^2} & \mathrm{~m}_3 \cdot \delta_{23} \\ \mathrm{~m}_1 \cdot \delta_{31} & \mathrm{~m}_2 \cdot \delta_{32} & \mathrm{~m}_3 \cdot \delta_{33}-\frac{1}{\omega^2} \end{array}\right)\right|=0 $$ (multiplicamos ambos lados por El/m) sustituimos \( \quad \omega=\frac{1}{\sqrt{\mathrm{x}}} \cdot \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}} \)\( \left[\begin{array}{ccc} 1 \cdot \frac{77}{76}-x & 1 \cdot\left(-\frac{79}{190}\right) & \frac{5}{2} \cdot \frac{110}{57} \\ 1 \cdot\left(-\frac{79}{190}\right) & 1 \cdot \frac{93}{95}-x & \frac{5}{2}\left(\frac{68}{95}\right) \\ 1 \cdot \frac{110}{57} & 1 \cdot\left(\frac{68}{95}\right) & \frac{5}{2} \cdot \frac{1136}{57}-x \end{array}\right]=0 \)
\( \left[\begin{array}{llc} \frac{77}{76}-\mathrm{x} & -\frac{79}{190} & \frac{275}{57} \\ -\frac{79}{190} & \frac{93}{95}-\mathrm{x} & -\frac{34}{19} \\ \frac{110}{57} & -\frac{68}{95} & \frac{2840}{57}-\mathrm{x} \end{array}\right]=0 \)
A continuación, usando el método de Sarrus calculamos el determinante de la matriz 3x3 anterior y lo simplificamos a una forma polinómica de grado 3 (como se muestra a continuación). Sería mejor si tuviéramos un programa que pueda simplificar esto por nosotros, como Mathcad.
\( -1 \cdot x^3+51.8167 \cdot x^2-89.4833 \cdot x+33.2632=0 \)
Raíces de la ecuación $$ \mathrm{x}_1=0.537 \quad \mathrm{x}_2=1.238 \quad \mathrm{x}_3=50.042 $$ ya que \( \mathrm{x}=\frac{1}{\omega^2} \frac{\text { EI }}{\mathrm{m}} \quad \omega=\frac{1}{\sqrt{\mathrm{x}}} \cdot \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}} \)
Frecuencias propias de vibración $$ \begin{aligned} &\omega_1=\frac{1}{\sqrt{x_3}}=0.14136 \cdot \sqrt{\frac{\text { EI }}{\mathrm{m}}} \\ &\omega_2=\frac{1}{\sqrt{x_2}}=0.899 \cdot \sqrt{\frac{E I}{\mathrm{~m}}} \\ &\omega_3=\frac{1}{\sqrt{x_1}}=1.3647 \cdot \sqrt{\frac{E I}{\mathrm{~m}}} \end{aligned} $$ Rigidez a la flexión $$ \begin{aligned} &\text { Para } \quad \mathrm{I}=2140 \cdot 10^{-8} \mathrm{~m}^4 \quad \text { y el módulo de Young para el acero } \quad \mathrm{E}=200 \cdot 10^9 \mathrm{~Pa} \\ &\mathrm{EI}=\mathrm{E} \cdot \mathrm{I}=4280000.000 \mathrm{Nm}^2 \quad \mathrm{~m}=100 \quad \mathrm{~kg} \\ &\omega_{1}=0.14136 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}=29.245 \quad \frac{\mathrm{rad}}{\mathrm{s}} \\ &\omega_{2}=0.899 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}=185.939 \frac{\mathrm{rad}}{\mathrm{s}} \\ &\omega_{3}=1.365 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}=282.33 \quad \frac{\mathrm{rad}}{\mathrm{s}} \end{aligned} $$
Determinación de la forma de vibración $$ \begin{aligned} &\left(\mathrm{m}_1 \cdot \delta_{11}-\mathrm{x}\right) \cdot \mathrm{A}_{11}+\mathrm{m}_2 \cdot \delta_{12} \cdot \mathrm{A}_{21}+\mathrm{m}_3 \cdot \delta_{13} \cdot \mathrm{A}_{31}=0 \\ &\mathrm{~m}_1 \cdot \delta_{12} \cdot \mathrm{A}_{11}+\left(\mathrm{m}_2 \cdot \delta_{22}-\mathrm{x}\right) \cdot \mathrm{A}_{21}+\mathrm{m}_3 \cdot \delta_{23} \cdot \mathrm{A}_{31}=0 \\ &\mathrm{~m}_1 \cdot \delta_{31} \cdot \mathrm{A}_{11}+\mathrm{m}_2 \cdot \delta_{32} \cdot \mathrm{A}_{21}+\left(\mathrm{m}_3 \cdot \delta_{33}-\mathrm{x}\right) \cdot \mathrm{A}_{31}=0 \end{aligned} $$
Resolvemos el sistema de ecuaciones anterior tres veces, una vez para "x" igual a "x1", otra para "x2" y otra para "x3".
Sustituyendo x, tenemos un sistema de 3 ecuaciones con tres incógnitas A11, A21, A31. Este sistema de ecuaciones siempre tiene infinitas soluciones, por lo que debemos mostrar una solución de ejemplo. Es decir, asumimos un valor de una de las incógnitas igual a 1, y luego nos quedamos con un sistema de tres ecuaciones con dos incógnitas restantes, donde si resolvemos las dos primeras ecuaciones, podemos calcular las otras dos incógnitas restantes.
para \( \quad \mathrm{x}=\mathrm{x}_1=0.537 \quad asumo \quad \mathrm{A}_{11}=1 \)
$$ \begin{aligned} &0.476+0.416 \mathrm{~A}_{21}+4.825 \cdot \mathrm{A}_{31}=0 \\ &-0.416+0.442 \mathrm{~A}_{21}-1.7895 \cdot \mathrm{A}_{31}=0 \\ &1.9298-0.716 \cdot \mathrm{A}_{21}+49.288 \cdot \mathrm{A}_{31}=0 \end{aligned} $$ Resuelvo el sistema de las dos primeras ecuaciones
$$ \begin{aligned} &\mathrm{A}_{21}=0.831 \\ &\mathrm{~A}_{31}=-0.027 \end{aligned} $$ Y la forma de vibración sería
 para \( \quad \mathrm{x}=\mathrm{x}_2=1.238 \quad asumo \quad \mathrm{A}_{12}=1 \)
para \( \quad \mathrm{x}=\mathrm{x}_2=1.238 \quad asumo \quad \mathrm{A}_{12}=1 \) $$ \begin{aligned} &-0.225-0.416 \cdot \mathrm{A}_{22}+4.825 \cdot \mathrm{A}_{32}=0 \\ &-0.416+0.442 \mathrm{~A}_{22}-1.7895 \cdot \mathrm{A}_{32}=0 \\ &1.9298-0.716 \cdot \mathrm{A}_{22}+49.288 \cdot \mathrm{A}_{32}=0 \end{aligned} $$ Resuelvo el sistema de las dos primeras ecuaciones
$$ \begin{aligned} &\mathrm{A}_{22}=0.905 \\ &\mathrm{~A}_{32}=-0.029 \end{aligned} $$ Y la forma de vibración sería &-0.416-0.259 \cdot \mathrm{A}_{22}-1.7895 \cdot \mathrm{A}_{32}=0 \\ &1.9298-0.716 \cdot \mathrm{A}_{22}+48.587 \cdot \mathrm{A}_{32}=0 \end{aligned} $$ We solve the system of the first two equations:
$$ \begin{aligned} &\mathrm{A}_{22}=-1.208 \\ &\mathrm{A}_{32}=-0.0575 \end{aligned} $$ Second form of vibration:

for \( \quad \mathrm{x}=\mathrm{x}_3=50.042 \quad I \quad assume \quad \mathrm{A}_{13}=1 \)
$$ \begin{gathered} -49.0286-0.416 \cdot \mathrm{A}_{23}+4.825 \cdot \mathrm{A}_{33}=0 \\ -0.416-49.063 \cdot \mathrm{A}_{23}-1.7895 \cdot \mathrm{A}_{33}=0 \\ 1.9298-0.716 \cdot \mathrm{A}_{23}-0.217 \cdot \mathrm{A}_{33}=0 \end{gathered} $$ We solve the system of the first two equations:
$$ \begin{aligned} &\mathrm{A}_{23}=-0.378 \\ &\mathrm{A}_{33}=10.130 \end{aligned} $$ Third form of vibration:

Checking the orthogonality conditions:
\begin{aligned} &\mathrm{m}_1 \cdot \mathrm{A}_{11} \cdot \mathrm{A}_{12}+\mathrm{m}_2 \cdot \mathrm{A}_{21} \cdot \mathrm{A}_{22}+\mathrm{m}_3 \cdot \mathrm{A}_{31} \cdot \mathrm{A}_{32}=0 \\ &\mathrm{~m}_1 \cdot \mathrm{A}_{12} \cdot \mathrm{A}_{13}+\mathrm{m}_2 \cdot \mathrm{A}_{22} \cdot \mathrm{A}_{23}+\mathrm{m}_3 \cdot \mathrm{A}_{32} \cdot \mathrm{A}_{33}=0 \\ &\mathrm{~m}_1 \cdot \mathrm{A}_{11} \cdot \mathrm{A}_{13}+\mathrm{m}_2 \cdot \mathrm{A}_{21} \cdot \mathrm{A}_{23}+\mathrm{m}_3 \cdot \mathrm{A}_{31} \cdot \mathrm{A}_{33}=0 \\ \end{aligned}
\begin{aligned} &1 \cdot 1 \cdot \mathrm{m}+1 \mathrm{~m} \cdot 0.831 \cdot(-1.208)+2.5 \mathrm{~m} \cdot(-0.027) \cdot(-0.0575) \rightarrow 0.00003 \mathrm{~m} \sim 0 \\ &1 \cdot 1 \cdot \mathrm{m}+1 \mathrm{~m} \cdot 0.831 \cdot(-1.208)+2.5 \mathrm{~m} \cdot(-0.027) \cdot(-0.0575) \rightarrow 0.00003 \mathrm{~m} \sim 0 \\ &1 \cdot 1 \cdot \mathrm{m}+1 \mathrm{~m} \cdot 0.831 \cdot(-0.378)+2.5 \mathrm{~m} \cdot(-0.027) \cdot 10.1297 \rightarrow 0.00213 \mathrm{~m} \sim 0 \end{aligned}
the check gives a positive result
Si tienes preguntas, comentarios, o crees que has encontrado un error en esta solución, por favor envíanos un mensaje a kontakt@edupanda.pl.
