Here is your translated HTML code: ```html

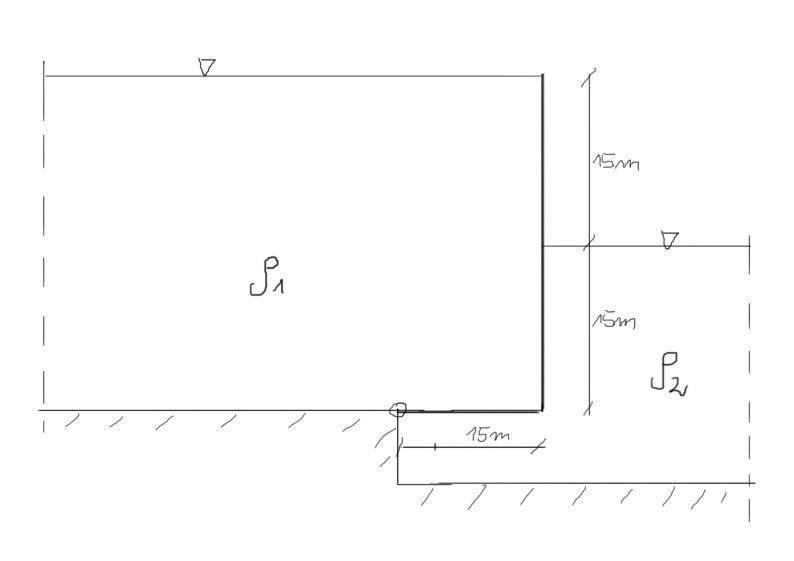
Dibuja los gráficos de presión y calcula el valor de la presión. Ancho del recipiente b=2m.

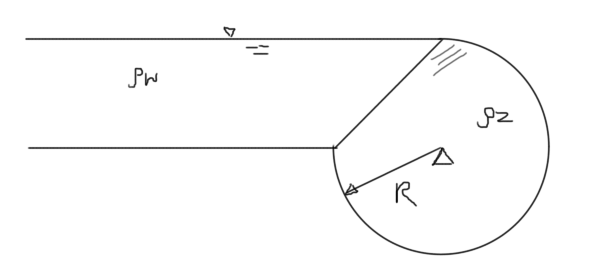
La válvula de radio R=1 m y longitud L=10 m cierra la esquina de un tanque rectangular, como se muestra en la figura. Calcular el momento necesario para mantener la válvula en la posición cerrada, si el tanque se llena con agua de densidad \(\rho_w=1 g/cm^3\), mientras que la densidad del material del cual está hecha la válvula es \(\rho_z=5 g/cm^3.\)

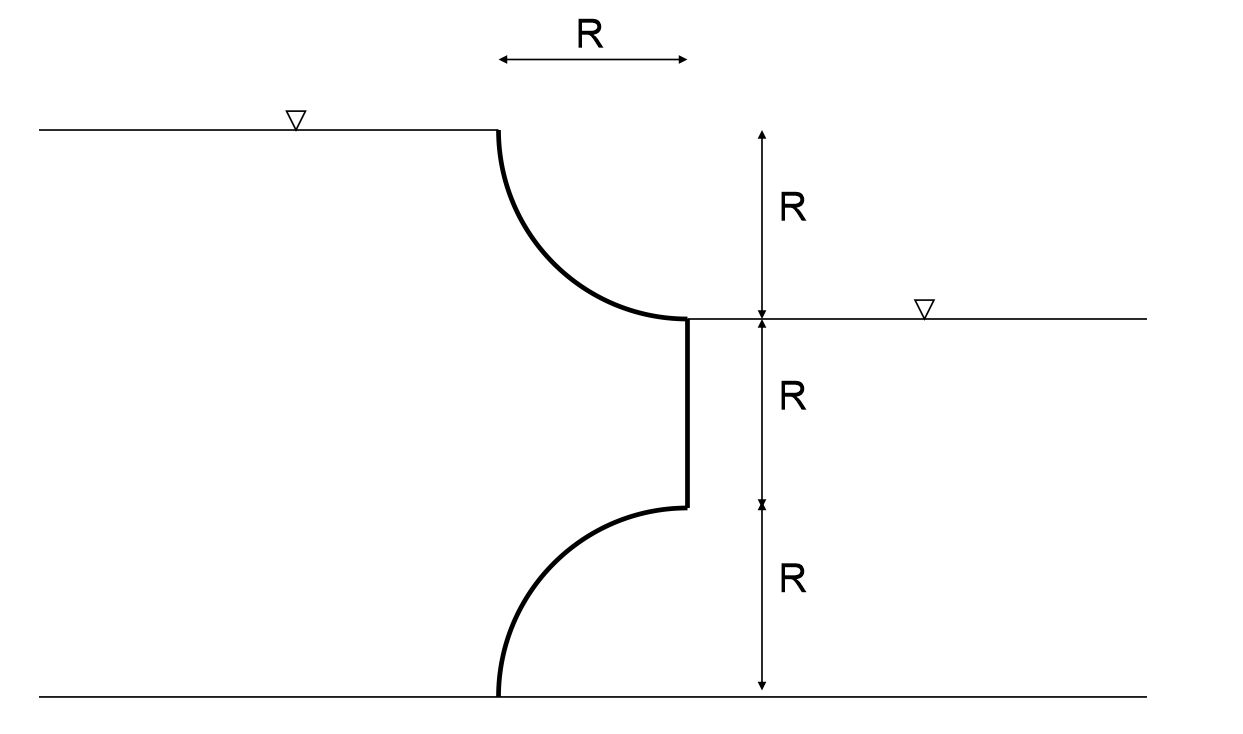
¿Cuántas veces debe ser mayor la densidad del líquido número 2 en comparación con la densidad del líquido número 1 para que se alcance el equilibrio? El ancho del recipiente \( b=1m \)

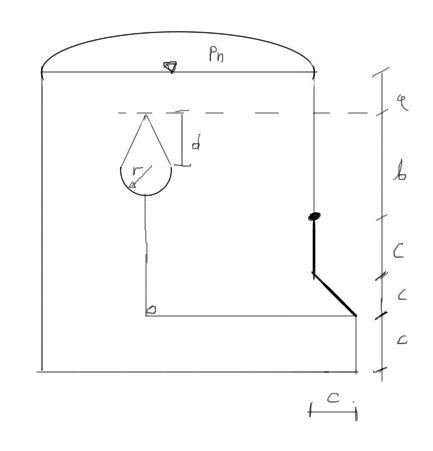
En el lateral de un tanque en el que hay una sobre presión \( p_n=4905 Pa \) hay un agujero. El agujero se cierra con una compuerta plana de ancho L mediante un flotador en forma de cono de altura d, conectado a una mitad de una esfera de radio r. La compuerta puede girar alrededor del punto O. El flotador tiene una masa m. La altura del vértice del flotador por encima del eje de rotación de la compuerta es b. El vértice del flotador está sumergido a una profundidad a. ¿Qué volumen V debe tener el flotador para garantizar el cierre del agujero como se muestra en la imagen?
Datos: \( a=0,25m, b=0,75m, c=0,5m, m=10kg, \rho_{H_2O} = 1000 kg/m^3, L=0,5m, p_n=4905Pa \)

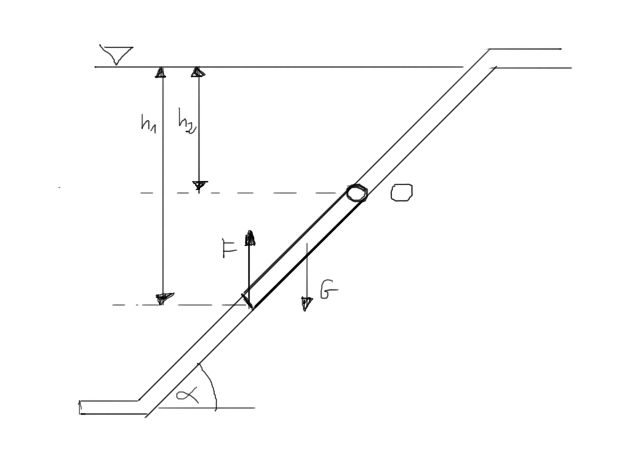
Cuadrada solapa de peso G cubre la abertura de liberación de un tanque de agua. La solapa tiene un eje de rotación O. Determinar la fuerza vertical F necesaria para levantar la solapa.
Datos:
\begin{aligned} &h_1 = 3.5 m\\ &h_2 = 2.5 m\\ &G = 200 N\\ &\alpha = 30^{\circ}\\ \end{aligned}

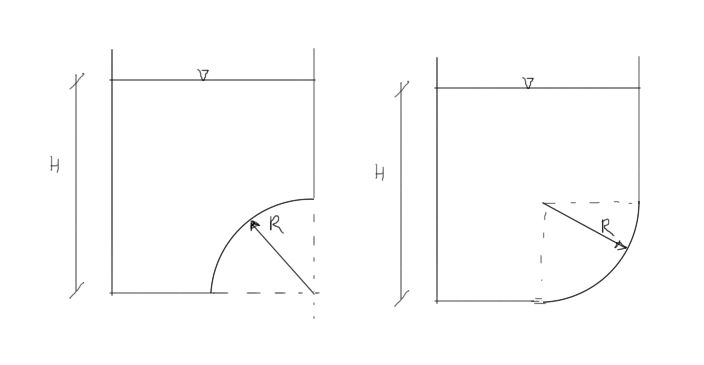
Zbiornik se cerró con una compuerta giratoria en forma de cuarto de cilindro con un radio R=1m y una longitud L=1m. Calcular la magnitud de la presión hidrostática ejercida sobre la compuerta en dos variantes mostradas en la figura. La densidad del agua \(\rho = 1000 kg/m^3\), la altura del agua en el tanque H=2m.

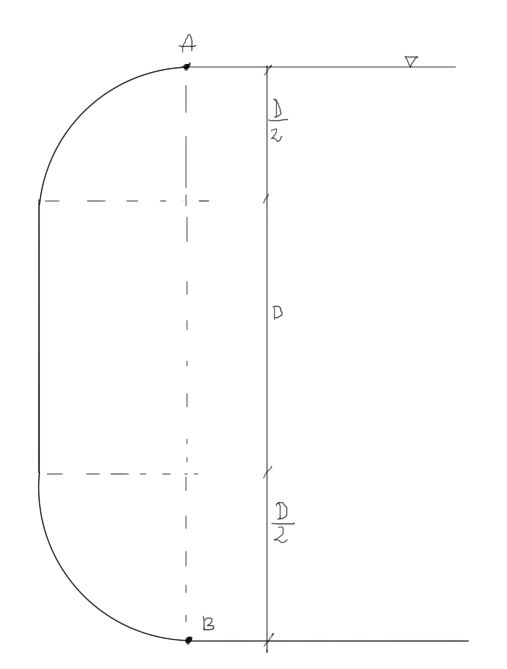
Calcule la presión del agua sobre la superficie AB de cierre, con la forma mostrada en la imagen. Datos: \begin{aligned} &D = 2m\\ &B = 5m\\ \end{aligned}

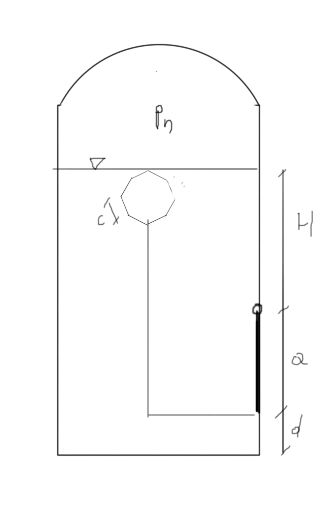
En el lateral del tanque, donde hay una presión \( p_n = 200 hPa \), hay una abertura rectangular de dimensiones \( a \times a/2 \). La abertura se cierra con una compuerta plana mediante un flotador con forma de prisma hexagonal de base c y altura f. El flotador tiene una masa \( m_p = 10 kg \). La elevación del agua sobre el eje de rotación de la compuerta es \( H \). ¿Qué volumen \( V \) debe tener el flotador para garantizar el cierre de la abertura cuando el flotador está completamente sumergido?
Datos:
\begin{aligned} &a=0,8 m\\ &b=1 m \\ &c=0,7 m\\ &H =2 m\\ \end{aligned}

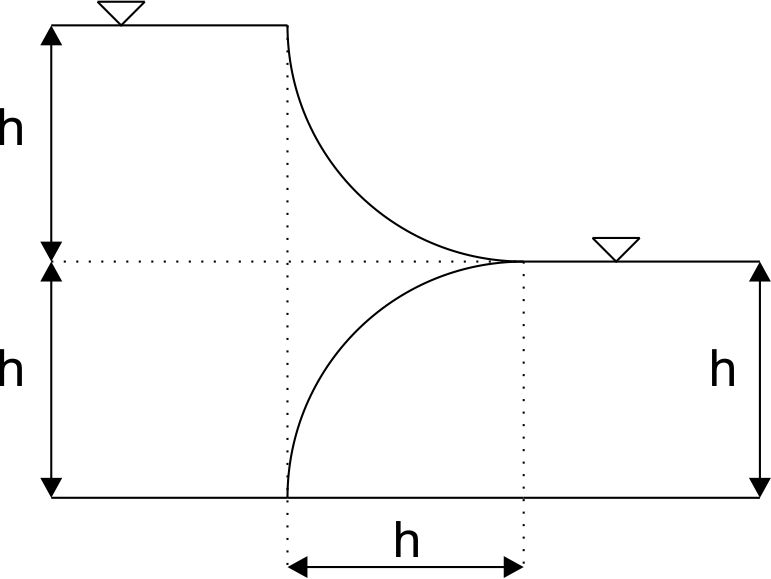
Para el diseño de la figura, calcule el valor de la presión, la posición del punto de presión y el ángulo bajo el cual actúa la fuerza de presión.
\begin{aligned} & \rho=1000 \frac{\mathrm{kg}}{\mathrm{m}^3} \\ & g=9.81 \frac{m}{s^2} \\ & \gamma=\rho \cdot g=9810 \frac{N}{m^3} \\ & h=1 m \\ & b=1 m \end{aligned}

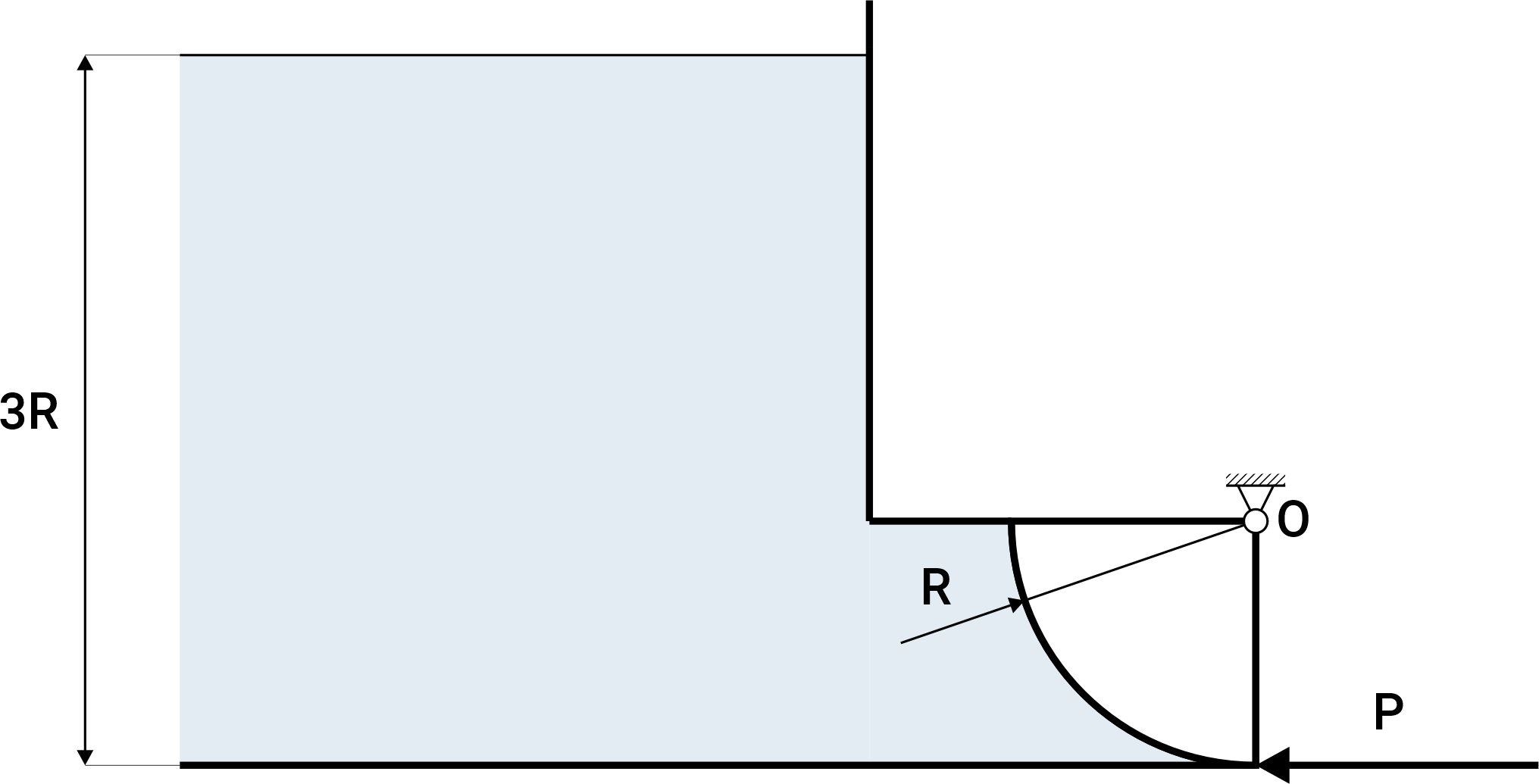
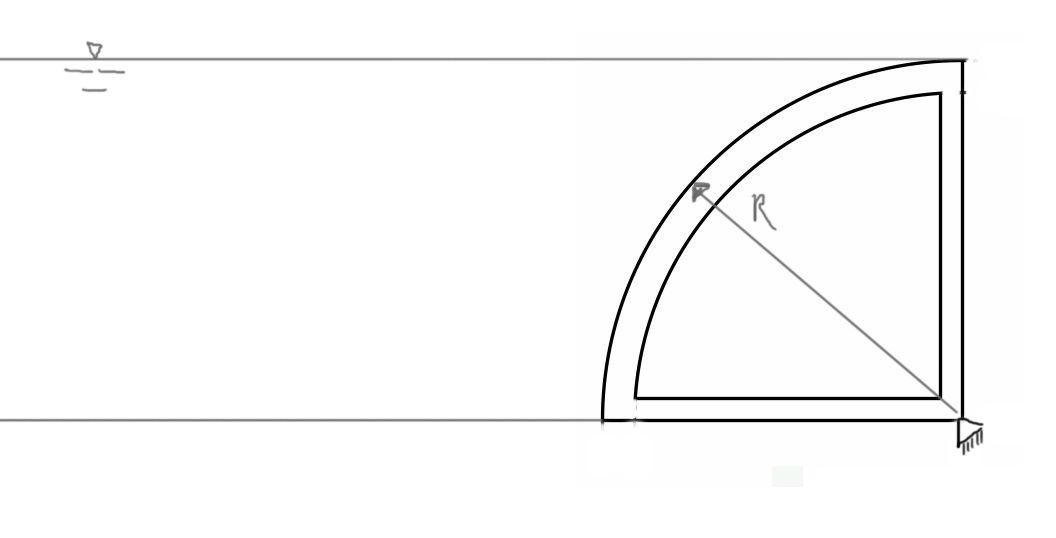
Válvula en forma de \(1 / 4\) de un cilindro, hecha de material con una densidad \(\rho_{\mathrm{z}}=7 \mathrm{~g} / \mathrm{cm}^3\), que puede girar alrededor del eje "O" y cerrar un tubo rectangular con una anchura \(\mathbf{B}=\mathbf{2} \mathbf{R}\) y altura \(\mathbf{R}=\mathbf{1 m}\), a través del cual el agua puede salir de la piscina. Calcular el valor de la fuerza \(\boldsymbol{P}\) necesaria para mantener la válvula en posición cerrada, si la piscina se llena de agua hasta una altura de \(3 R\). Tomar la densidad del agua como \(\rho=1 \mathrm{~g} / \mathrm{cm}^3\).