Lista zadań
Exemple 1
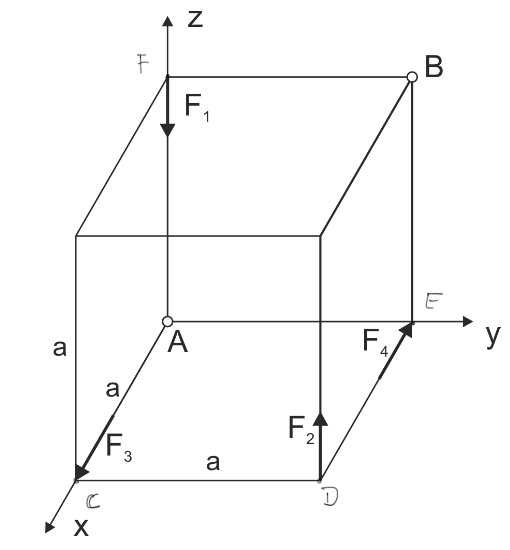
Un système de forces spatiales est donné. a) Réduisez le système en point A b) Réduisez le système en point B c) Réduisez le système à sa forme la plus simple. \begin{aligned} &F_{1}=2 \mathrm{kN} \\ &F_{2}=2 \mathrm{kN} \\ &F_{3}=2 \mathrm{kN} \\ &F_{4}=2 \mathrm{kN} \\ &a=1 \mathrm{~m} \end{aligned}
Exemple 2
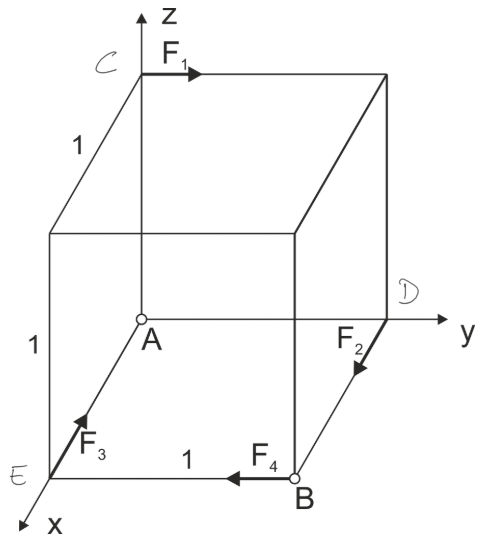
Un système de forces spatiales est donné. a) Réduisez le système au point A b) Réduisez le système au point B c) Réduisez le système à sa forme la plus simple. Dessinez le résultat de la réduction
\begin{aligned} &F_{1}=5 k N \\ &F_{2}=2 k N \\ &F_{3}=2 k N \\ &F_{4}=5 k N \end{aligned}Exemple 3
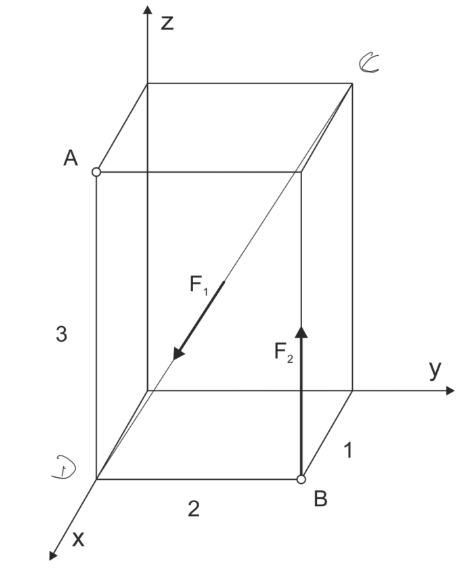
D'un ensemble de forces spatiales est donné. a) Réduisez l'ensemble au point A b) Réduisez l'ensemble au point B c) Réduisez l'ensemble à sa forme la plus simple.
\begin{aligned} &F_{1}=\sqrt{14} kN \\ &F_{2}=3 kN \end{aligned}Exemple 4
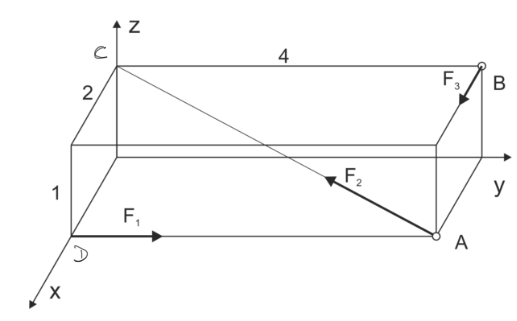
Un système de forces spatiales est donné. a) Réduire le système au point A b) Réduire le système au point B c) Réduire le système à sa forme la plus simple.
\begin{aligned} &F_{1}=1 k N \\ &F_{2}=2 \sqrt{21} k N \\ &F_{3}=4 k N \end{aligned}Exemple 5
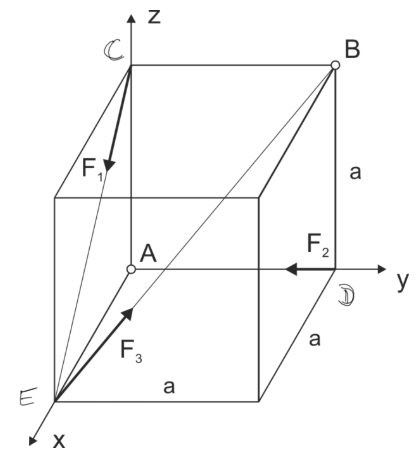
Dans cet exemple, nous avons un système de forces en trois dimensions. a) Réduisez le système en point A. b) Réduisez le système en point B. c) Réduisez le système à sa forme la plus simple.
\begin{aligned} &F_{1}=10 P \\ &F_{2}=\sqrt{2} P \\ &F_{3}=\sqrt{6} P \end{aligned}