Lista zadań
Ejemplo 1
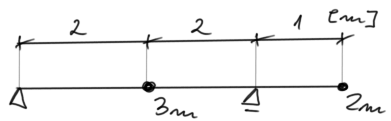
Para el dado travesaño, determinar las frecuencias naturales de vibración y dibujar sus modos de vibración. Verificar la condición de ortogonalidad. Datos: \( EI=3,5\cdot 10^5 kNm^2 , m=750kg \)
Ejemplo 2
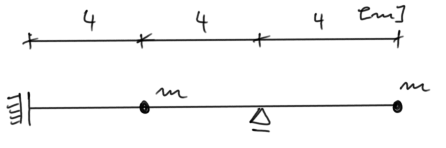
Para la viga dada, determinar las frecuencias naturales de vibración y dibujar sus modos de vibración. Verificar la condición de ortogonalidad.
Ejemplo 3
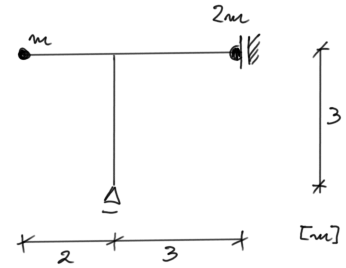
Para el marco dado, determinar las frecuencias naturales de vibración y dibujar sus modos de vibración. Comprobar la condición de ortogonalidad. Estimar la frecuencia natural fundamental utilizando métodos aproximados.
Ejemplo 4
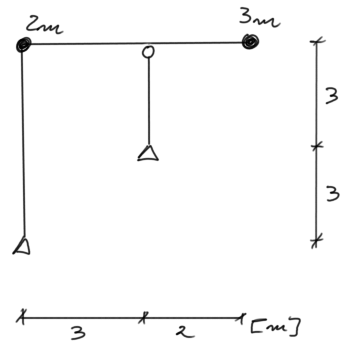
Para el marco dado, determinar las frecuencias naturales de vibración y dibujar sus modos de vibración. Verificar la condición de ortogonalidad. Estimar la frecuencia natural más baja utilizando métodos aproximados.
Ejemplo 5
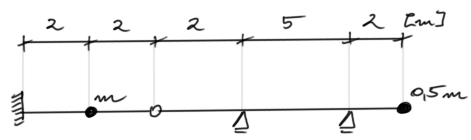
Para la viga dada, determinar las frecuencias propias de vibración y dibujar sus modos de vibración. Verificar la condición de ortogonalidad. Aproxime la frecuencia propia fundamental utilizando métodos aproximados.
Ejemplo 6

Para el marco dado, determinar las frecuencias naturales de vibración y dibujar sus formas modales. Verificar la condición de ortogonalidad. Estimar la frecuencia natural fundamental utilizando métodos aproximados.
Ejemplo 7

Para el marco dado, determinar las frecuencias naturales de vibración y dibujar sus formas. Comprobar la condición de ortogonalidad. Estimar la frecuencia natural fundamental utilizando métodos aproximados.
Ejemplo 8
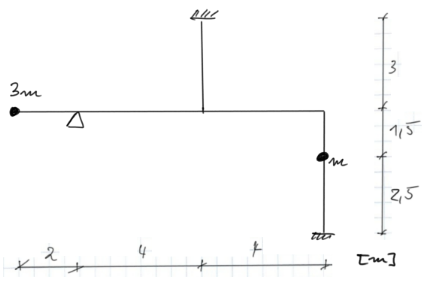
Para el marco dado, determinar las frecuencias naturales de vibración y dibujar sus formas. Verificar la condición de ortogonalidad. Estimar la frecuencia natural básica mediante métodos aproximados.
Ejemplo 9
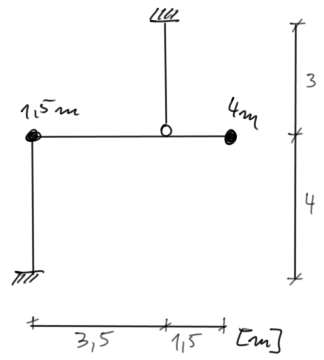
Para el marco dado, determinar las frecuencias naturales de vibración y dibujar sus modos de vibración. Verificar la condición de ortogonalidad. Estimar la frecuencia natural fundamental utilizando métodos aproximados.
Ejemplo 10
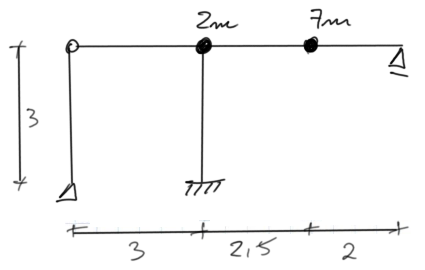
Para el marco dado, determinar las frecuencias de oscilación propia y dibujar sus formas. Comprobar la condición de ortogonalidad. Estimar la frecuencia propia fundamental utilizando métodos aproximados.