Solución
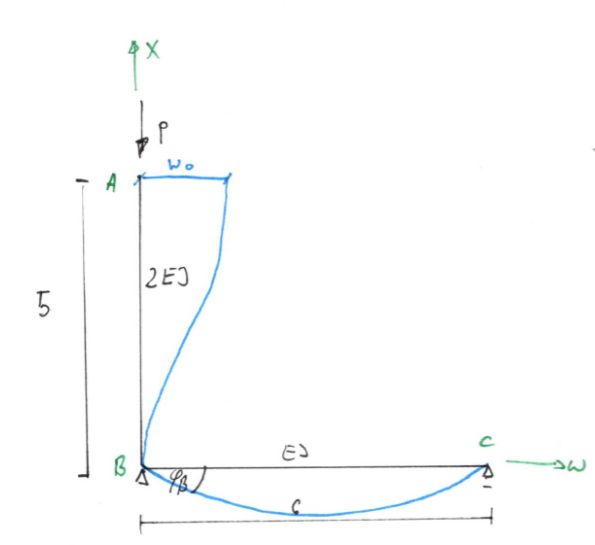
Ecuación diferencial de la línea de flexión
\begin{aligned} 2 E I w^{\prime \prime}=-M(x)=-(P \cdot(w_{0}-w)) \end{aligned}Transformamos a una ecuación diferencial de segundo orden en forma típica
\begin{aligned} &\alpha=\sqrt{\frac{P}{2 E I}} \\ &w^{\prime \prime}+\alpha^{2} w-\alpha^{2} w_{0}=0 \end{aligned}La solución de esta ecuación es una función:
\begin{aligned} &w=C_{1} \cdot \sin (\alpha \cdot x)+C_{2} \cdot \cos (\alpha \cdot x)+w_{0} \\ &w^{\prime}=C_{1} \cdot \alpha \cdot \cos (\alpha \cdot x)-C_{2} \cdot \alpha \cdot \sin (\alpha \cdot x)+w_{0} \cdot x \end{aligned}Condiciones de frontera para la barra BC - falta /( \varphi_B /), utilizaremos por ejemplo el método de Clebsch
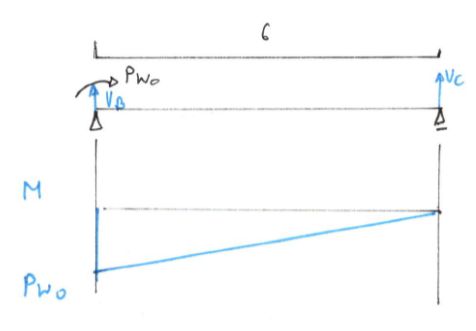 \begin{aligned}
&\Sigma M_{C}=0 \\
&V_{B} \cdot 6+P \cdot w_{0}=0 \\
&V_{B}=\frac{-P \cdot w_{0}}{6} \\
&M_{BC}=P \cdot w_{0}-\frac{P \cdot w_{0}}{6} \cdot x \\
&E I w^{\prime \prime}=-M_{BC}=-P \cdot w_{0}+\frac{P \cdot w_{0}}{6} \cdot x \\
&E I w^{\prime}=-P \cdot w_{0} \cdot x+\frac{P \cdot w_{0}}{6} \cdot \frac{x^{2}}{2}+C \\
&E I w=-P \cdot w_{0} \cdot \frac{x^{2}}{2}+\frac{P \cdot w_{0}}{6} \cdot \frac{x^{3}}{6}+C \cdot x+D
\end{aligned}
\begin{aligned}
&\Sigma M_{C}=0 \\
&V_{B} \cdot 6+P \cdot w_{0}=0 \\
&V_{B}=\frac{-P \cdot w_{0}}{6} \\
&M_{BC}=P \cdot w_{0}-\frac{P \cdot w_{0}}{6} \cdot x \\
&E I w^{\prime \prime}=-M_{BC}=-P \cdot w_{0}+\frac{P \cdot w_{0}}{6} \cdot x \\
&E I w^{\prime}=-P \cdot w_{0} \cdot x+\frac{P \cdot w_{0}}{6} \cdot \frac{x^{2}}{2}+C \\
&E I w=-P \cdot w_{0} \cdot \frac{x^{2}}{2}+\frac{P \cdot w_{0}}{6} \cdot \frac{x^{3}}{6}+C \cdot x+D
\end{aligned}
Condiciones de frontera
\begin{aligned} &x=0 \quad w=0 \quad D=0 \\ &x=6 \quad w=0 \quad C=? \\ &0=-P \cdot w_{0} \cdot \frac{6^{2}}{2}+\frac{P \cdot w_{0}}{6} \cdot \frac{6^{3}}{6}+C \cdot 6+0 \\ &C=2 P \cdot w_{0} \end{aligned}Por lo tanto, finalmente
\begin{aligned} &E I w^{\prime}=-P \cdot w_{0} \cdot x+\frac{P \cdot w_{0}}{6} \cdot \frac{x^{2}}{2}+2 P \cdot w_{0} \\ &x=0 \\ &w^{\prime}=\frac{2}{E I} P \cdot w_{0} \end{aligned}Volviendo a la ecuación diferencial
\begin{aligned} &x=0\\ &w=0\\ &0=C_{2}+w_{0}\\ &x=0\\ &w^{\prime}=\frac{2 \cdot P \cdot w_{0}}{E I}\\ &\frac{2 \cdot P \cdot w_{0}}{E I}=C_{1} \cdot \alpha\\ &C_{1}=\frac{2 \cdot P \cdot w_{0}}{E I \cdot \alpha}\\ &C_{2}=-w_{0}\\ &w=\frac{2 \cdot P \cdot w_{0}}{E I \cdot \alpha} \sin (\alpha \cdot x)-w_{0} \cdot \cos (\alpha \cdot x)+w_{0}\\ \end{aligned}Según las suposiciones del problema:
\begin{aligned} &x=l \quad w=w_{0} \\ &w_{0}=\frac{2 \cdot P \cdot w_{0}}{E I \cdot \alpha} \sin (\alpha \cdot l)-w_{0} \cdot \cos (\alpha \cdot l)+w_{0} \\ &0=\frac{2 \cdot P \cdot w_{0}}{E I \cdot \alpha} \sin (\alpha \cdot l)-w_{0} \cdot \cos (\alpha \cdot l) \end{aligned}Dado que /( w_0 \neq 0 /)
\begin{aligned} &0=\frac{2 \cdot P}{E I \cdot \alpha} \sin (\alpha \cdot l)-\cos (\alpha \cdot l) \\ &\alpha^{2}=\frac{P}{2 E I} \quad \frac{P}{E I}=2 \alpha^{2} \\ &0=4 \alpha \sin (\alpha \cdot l)-\cos (\alpha \cdot l) \\ &\cot (\alpha \cdot l)=4 \alpha \\ &\cot (5 \alpha)=4 \alpha \end{aligned}La raíz más pequeña de esta ecuación y su fuerza crítica correspondiente:
\begin{aligned} &\alpha=0.18615\\ &P_{cr}=2 E I \cdot \alpha^{2}\\ &P_{cr}=0.0693 E I\\ \end{aligned}Longitud de pandeo
\begin{aligned} &P_{cr}=\frac{\pi^{2} E I}{l_{eff}{ }^{2}}=\frac{\pi^{2} E I}{(k \cdot l)^{2}} \\ &0.0693 E I=\frac{\pi^{2} E I}{(\mu \cdot 5)^{2}} \\ &\mu=2.387 \end{aligned}