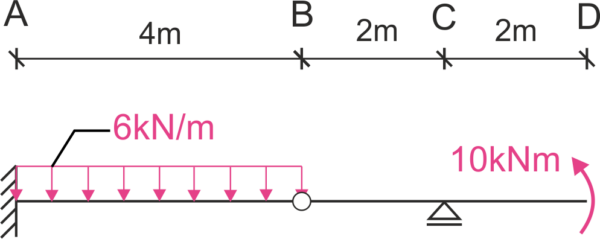
Calculer le déplacement vertical du point D \(\Delta_D.\) Prendre en compte l'effet des moments de flexion et des forces de cisaillement.

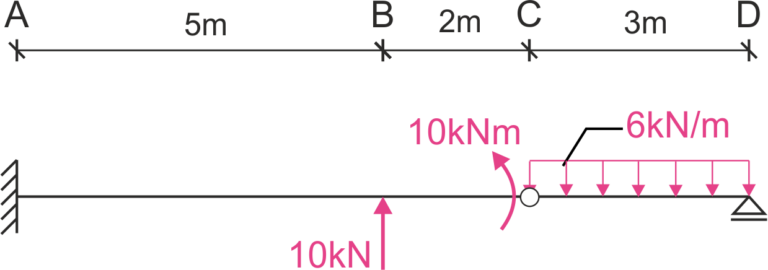
Calculer l'angle de rotation du point D \(\varphi_D.\) Prenez en compte l'influence des moments de flexion et des forces de cisaillement.

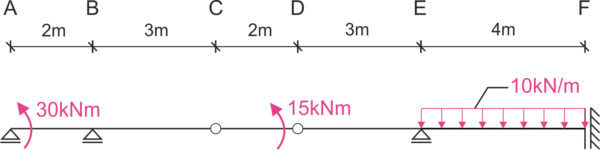
Calculer le déplacement vertical du point C \( \Delta_C \), le déplacement vertical du point D \( \Delta_D \), le changement d'angle de rotation du point C \( \Delta\varphi_C \). E=210GPa, I=6500cm^4. N'inclure que l'effet des moments de flexion.

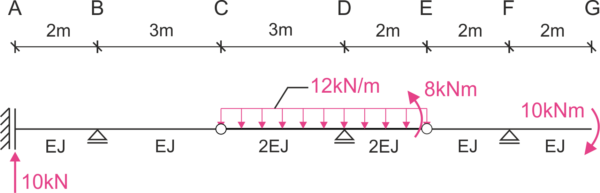
Calculer le déplacement vertical du point C \( \Delta_C \), l'angle de rotation au point G \(\varphi_G \) et le changement d'angle de rotation au point C \( \Delta\varphi_C. E=210 GPa, I=7500cm^4 \) Considérez uniquement l'influence des moments de flexion.

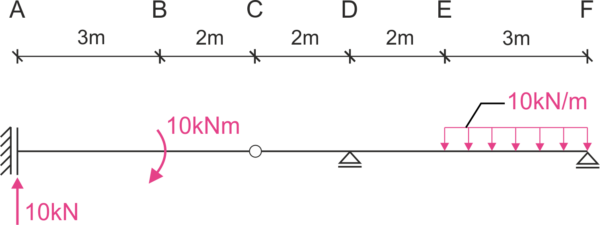
Calculate the vertical displacement of point A \( \Delta_A\), the vertical displacement of point E \( \Delta_E\), the rotation angle at point F \( \varphi_F\), and the change in rotation angle at point C \( \Delta\varphi_C\). Take into account the influence of bending moments. \( E=200 GPa, I=5000cm^4 \)

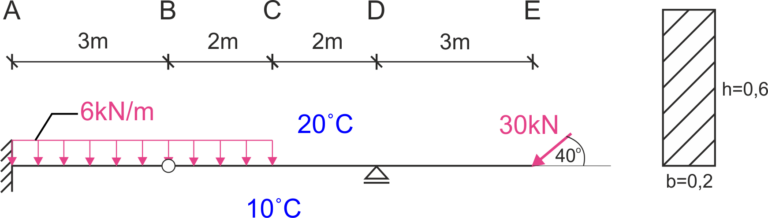
Calculez le déplacement vertical du point C \( \Delta_C\), le déplacement horizontal du point E \( \Delta_E\) et le changement d'angle de rotation au point B \( \Delta\varphi_B\). Tenez compte de l'effet des moments de flexion, des forces normales et de l'effet de la température. Données : \( b=0,2m, h=0,6m, E=205 GPa, \nu=0,3, t_g=20^oC, t_d=10^oC, \alpha=1,2\cdot 10^{-5}, \kappa=1,2 \)

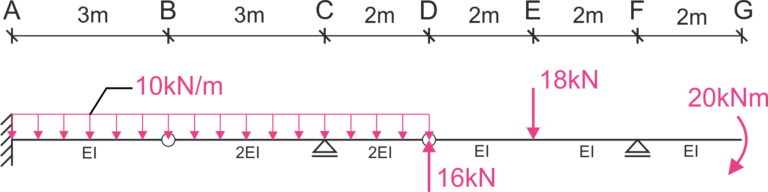
Calculer l'angle de rotation du nœud C \(\varphi_C\), le déplacement vertical du point G \(\Delta_G\), le déplacement vertical du point D \(\Delta_D\) et le changement d'angle de rotation au point D \(\Delta\varphi_D.\) Tenir compte de l'effet des moments de flexion en prenant en compte les caractéristiques différentes des sections. \(E=210GPa, I=7650 cm^4\)