Exemple 1

Pour la configuration donnée, déterminez les diagrammes des forces internes en utilisant la méthode des déplacements.

single-task-hero-img

Solution

1. Détermination du degré d'indéterminabilité cinématique :

\begin{aligned} &SKN=1\\ \end{aligned}

2. Sélection du système de base de la méthode des déformations :

3. Graphiques et détermination des coefficients et termes indépendants de l'équation :

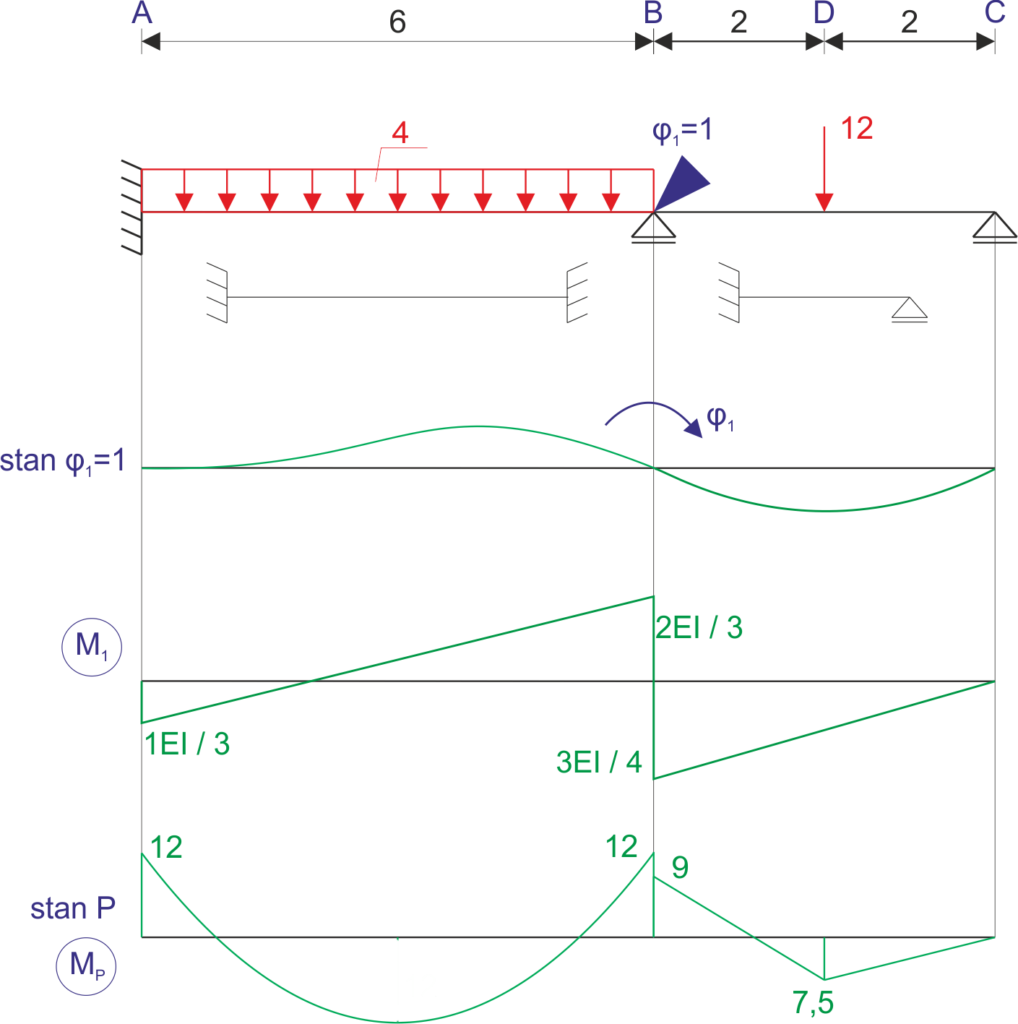
Détermination des coefficients du système de base de la méthode des déformations

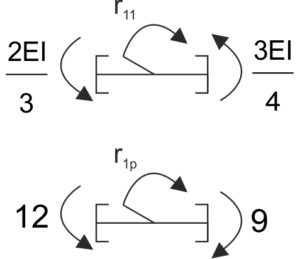\begin{aligned} &r_{11}=\frac{2EI}{3} +\frac{3EI}{4} =\frac{17EI}{12}\\ &r_{1p}=12-9=3\\ \end{aligned}

Système d'équations :

\begin{aligned} &r_{11}\cdot\varphi_{1} +r_{1p}=0\\ \end{aligned} \begin{aligned} &\varphi_{1}=-\frac{r_{1p}}{r_{11}}=-\frac{36}{17EI}\\ \\ &M_{ost}=M_{p}+\varphi_{1}\cdot M_{1}\\ &M_{AB}=-12-\frac{1}{3}\cdot \left(-\frac{36}{17}\right)=-12,706\\ &M_{BA}=12+\frac{2}{3}\cdot \left(-\frac{36}{17}\right)=-10,588\\ &M_{BC}=-9+\frac{3}{4}\cdot \left(-\frac{36}{17}\right)=-10,588\\ &M_{CB}=0\\ \end{aligned}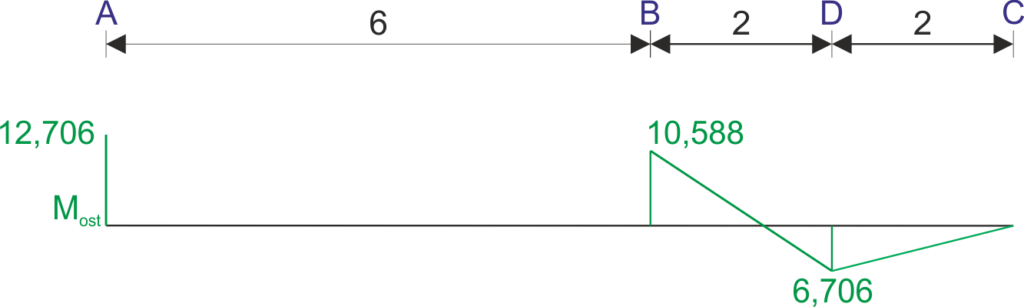

Élément AB :

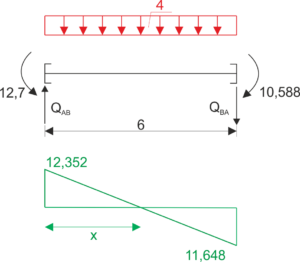\begin{aligned} &\sum{M_{B}}=0\\ &{Q_{AB}}\cdot 6+10,588-12,7-4\cdot6\cdot3=0\\ &{Q_{AB}}=12,352\\ &\sum{M_{A}}=0\\ &{Q_{BA}}\cdot 6+10,588+4\cdot 6\cdot 3-12,7=0\\ &{Q_{BA}}=-11,648\\ &\frac{12,352}{x}=\frac{11,648}{6-x}\\ &74,112-12,352x=11,648\\ &x=3,088\\ &M_{max}=-12,7+0,5\cdot 12,352\cdot 3,088\\ \end{aligned}

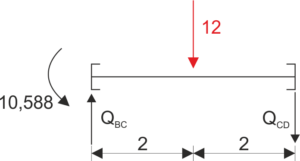
Élément BD :

\begin{aligned} &\sum{M_{C}}=0\\ &{Q_{BC}}\cdot 4-12\cdot 2-10,588=0\\ &{Q_{BC}}=8,647\\ &\sum y=0\\ &8,647-12-Q_{CD}=0\\ &Q_{CD}=-3,353\\ \end{aligned}

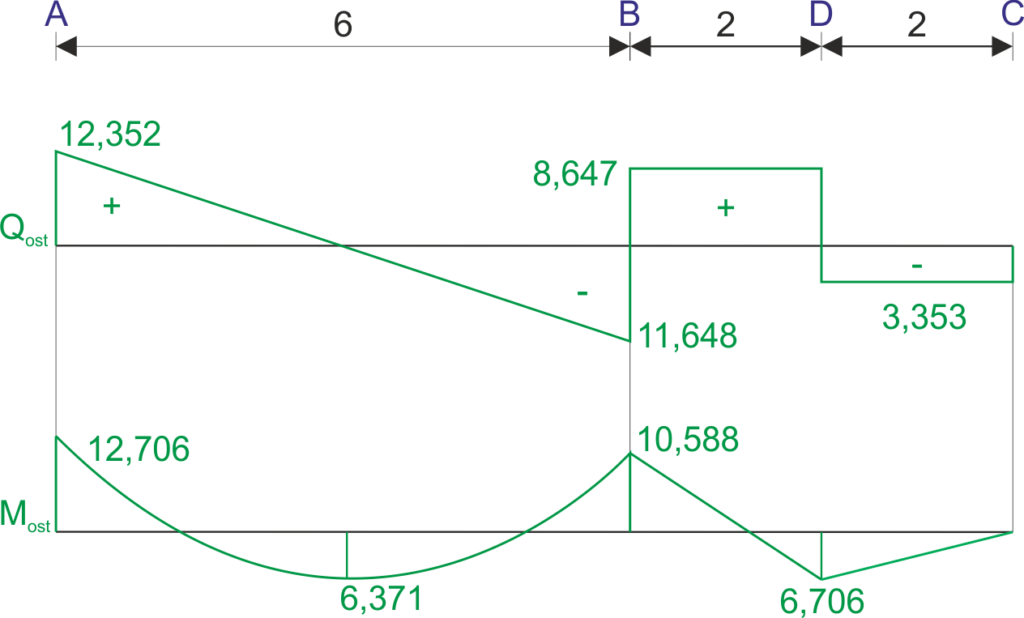
Graphiques finaux des forces internes