1. Identification of characteristic points and reactions on supports

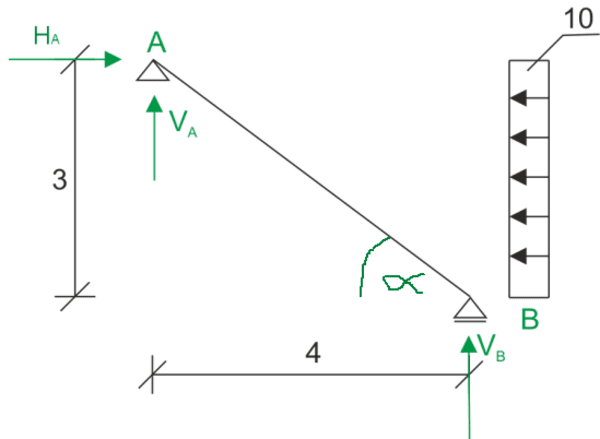\begin{aligned} &\sum{M_A}=0\\ &-V_B\cdot 4+10\cdot 3\cdot 1,5=0 &V_{B}=11,25\\ &\sum{F_Y}=0\\ &V_{A}=-11,25\\ &\sum{M_B}=0\\ &-V_{A}\cdot 4+H_{A}\cdot 3-10\cdot 3\cdot 1,5=0 &H_{A}=30\\ \\ \end{aligned} \begin{aligned} &sin\alpha=0,6\\ &cos\alpha=0,8\\ \\ \end{aligned}

We decompose the reactions into components along and perpendicular to the rod axis:

Section AB

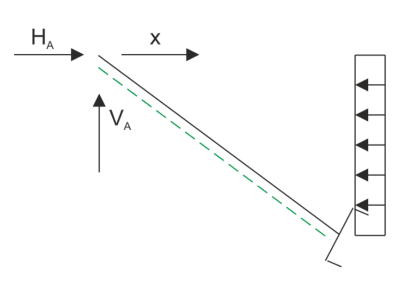\begin{aligned} &N_{AB}=-H_{A}\cdot cos\alpha+V_{A}\cdot sin\alpha+10\cdot cos\alpha\cdot y\\ &N_{A(0)}=-30,75\\ &N_{B(2)}=-6,75\\ &Q_{AB}=H_{A}\cdot sin\alpha+V_{A}\cdot cos\alpha-10\cdot sin\alpha\cdot y\\ &Q_{A(0)}=9\\ &Q_{B(4)}=-9\\ \\ &M_{AB}=H_{A}\cdot y+V_{A}\cdot x-10\cdot \frac{y^2}{2}\\ &M_{A(0)}=0\\ &M_{B(4)}=0\\ &M_{MAX(2)}=11,25 \\ \end{aligned}

Internal force diagrams