Lista zadań
Przykład 1
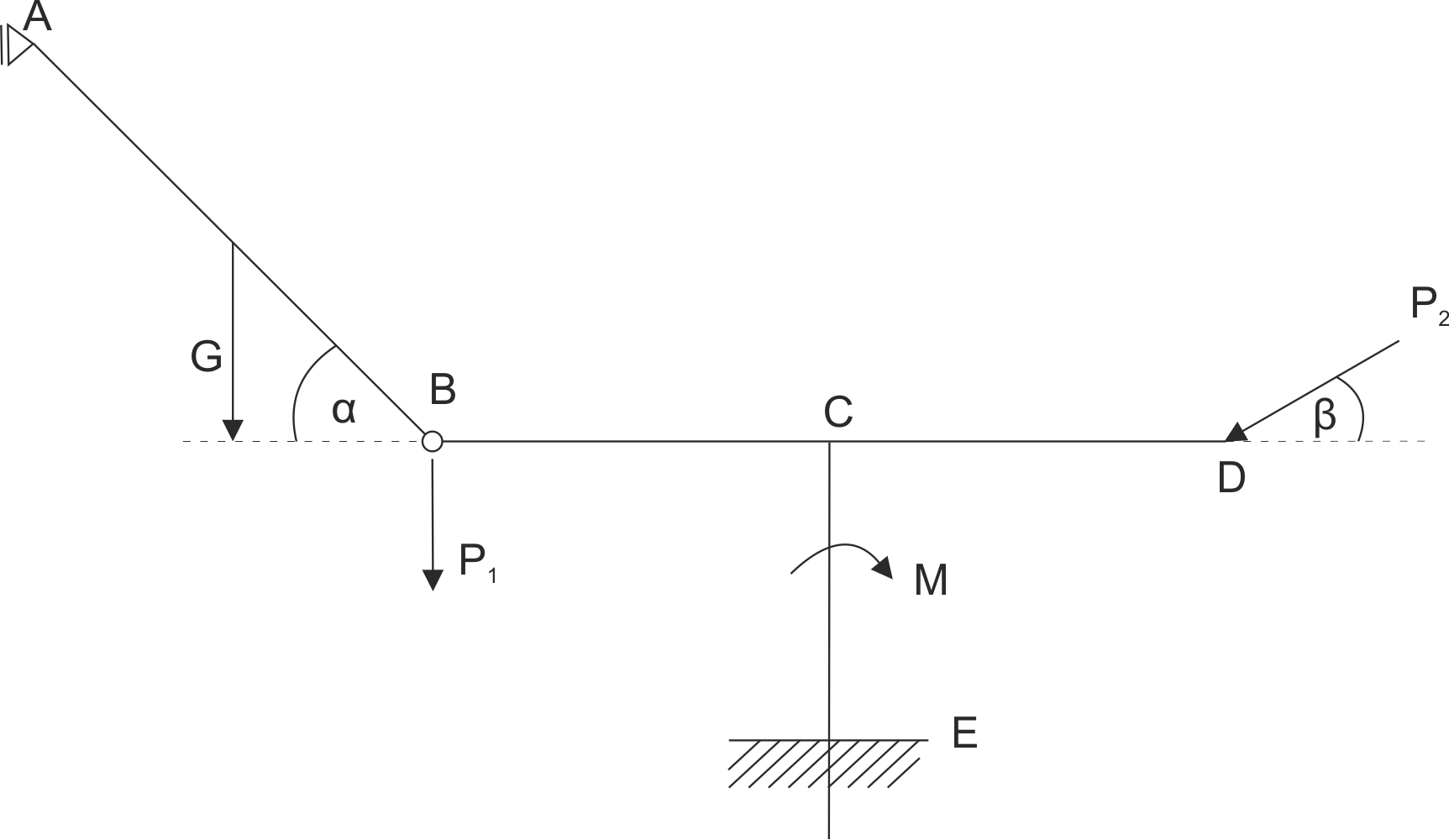
Dana jest rama podparta jak na rysunku. Uwolnij układ od więzów i zapisz równania równowagi.
Przykład 2
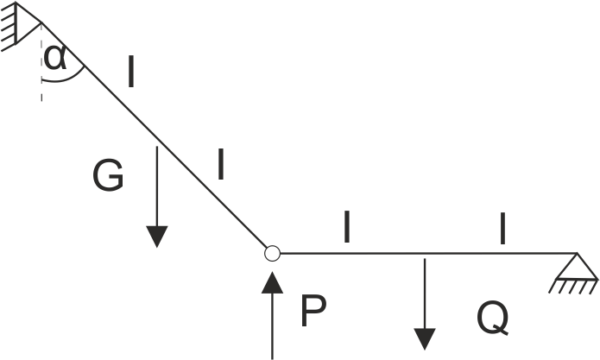
Dana jest rama podparta jak na rysunku. Uwolnij układ od więzów i zapisz równania równowagi.
Przykład 3
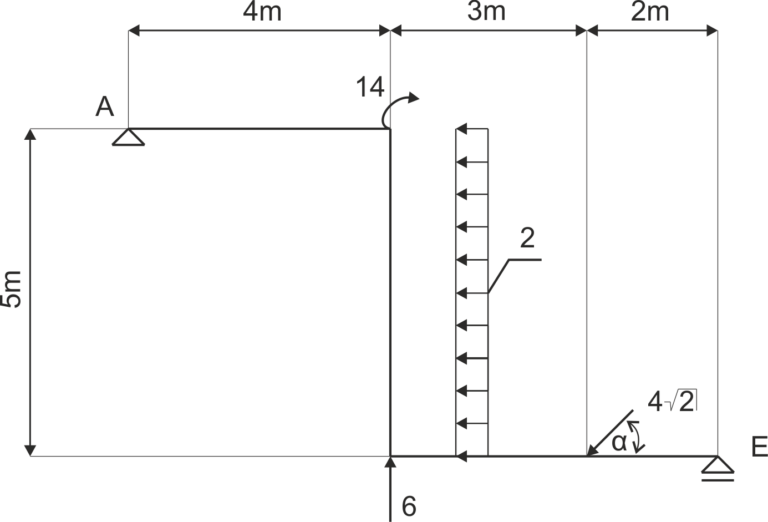
Dana jest rama podparta jak na rysunku. Uwolnij układ od więzów i zapisz równania równowagi. \( \alpha = 45^0 \).
Przykład 4
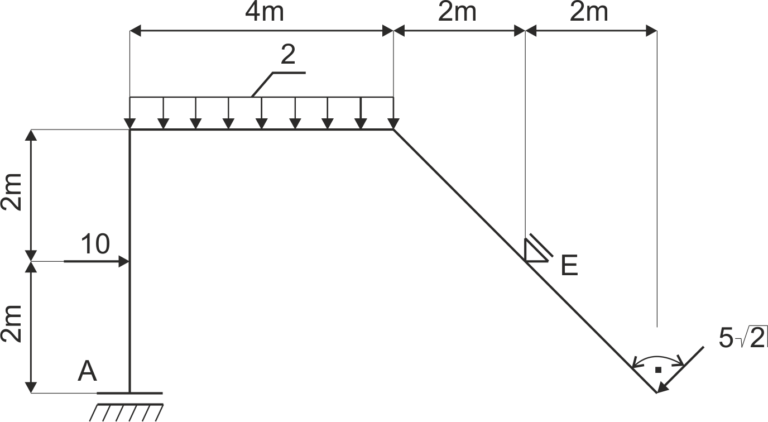
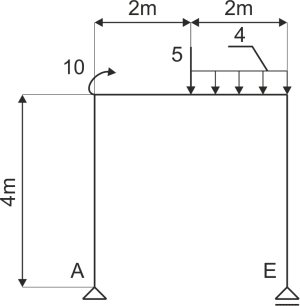
Dana jest rama podparta jak na rysunku. Uwolnij układ od więzów i zapisz równania równowagi.
Przykład 5
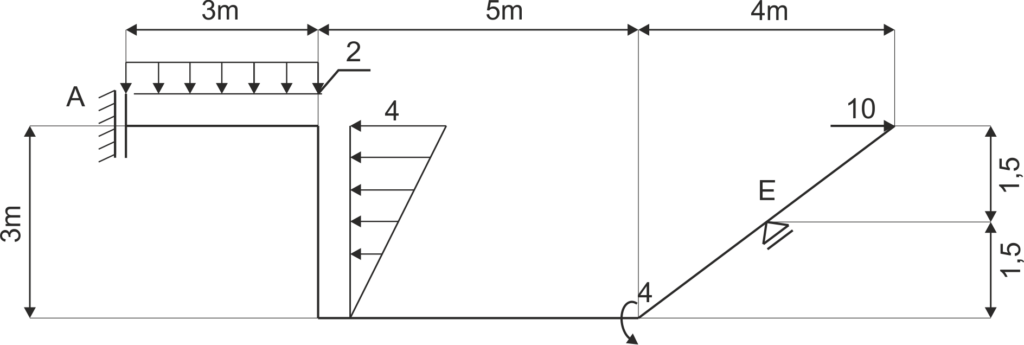
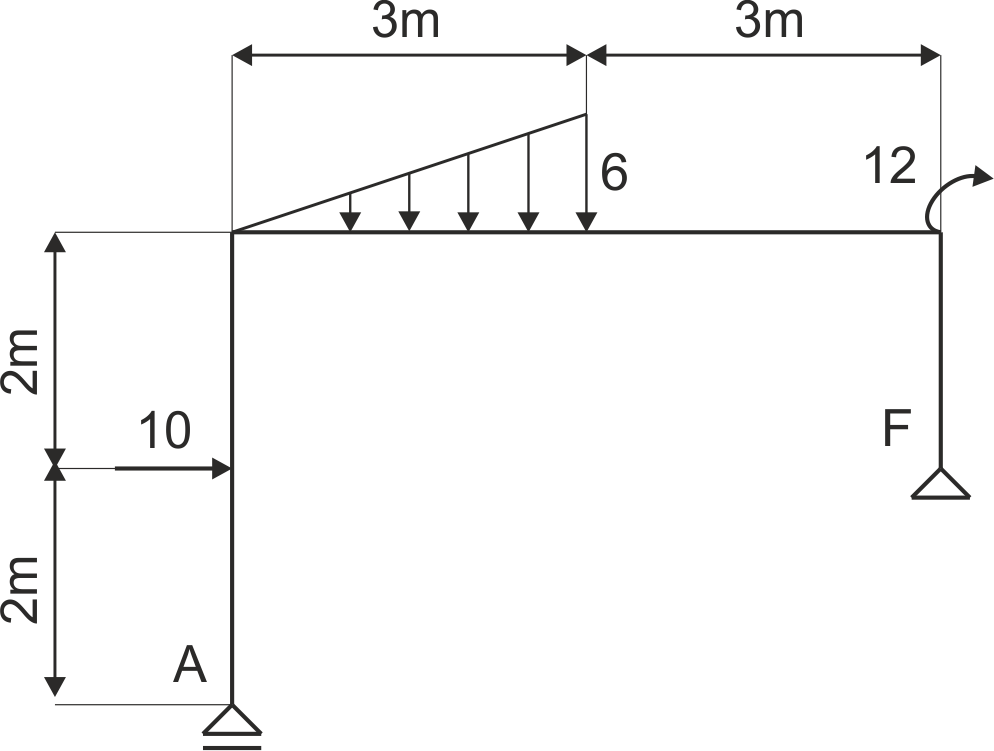
Dana jest rama podparta jak na rysunku. Uwolnij układ od więzów i zapisz równania równowagi.
Przykład 6
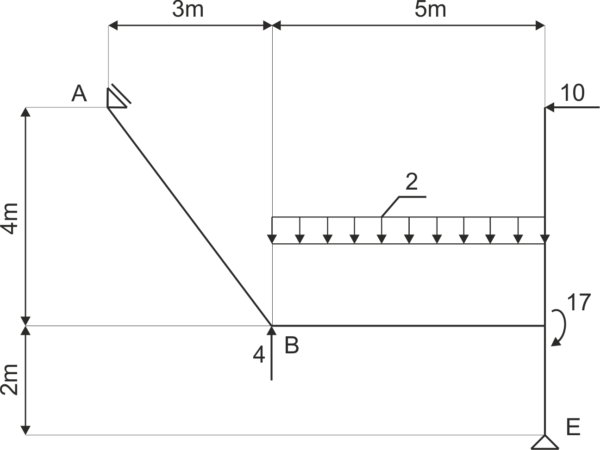
Dana jest rama podparta jak na rysunku. Uwolnij układ od więzów i zapisz równania równowagi.
Przykład 7
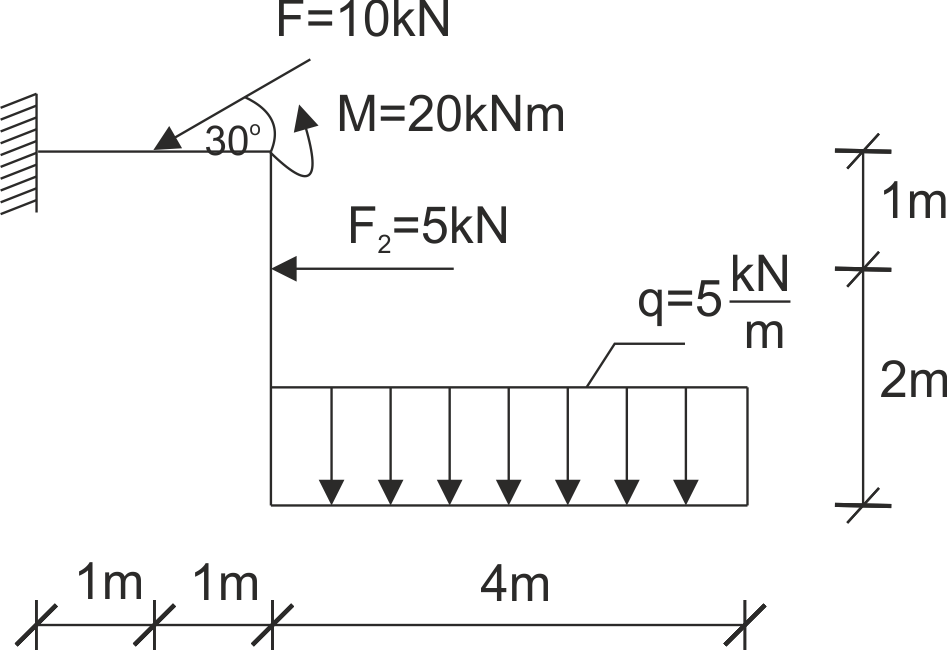
Dana jest rama podparta jak na rysunku. Uwolnij układ od więzów i zapisz równania równowagi.
Przykład 8
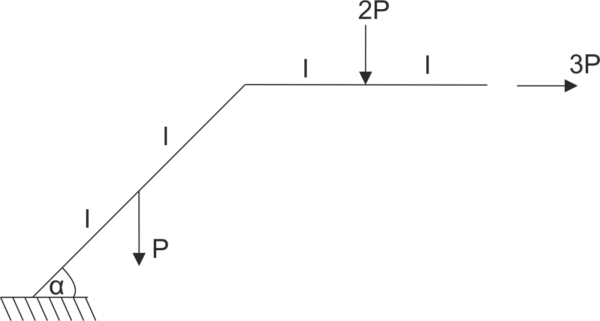
Dana jest rama podparta jak na rysunku. Uwolnij układ od więzów i zapisz równania równowagi.
Przykład 13
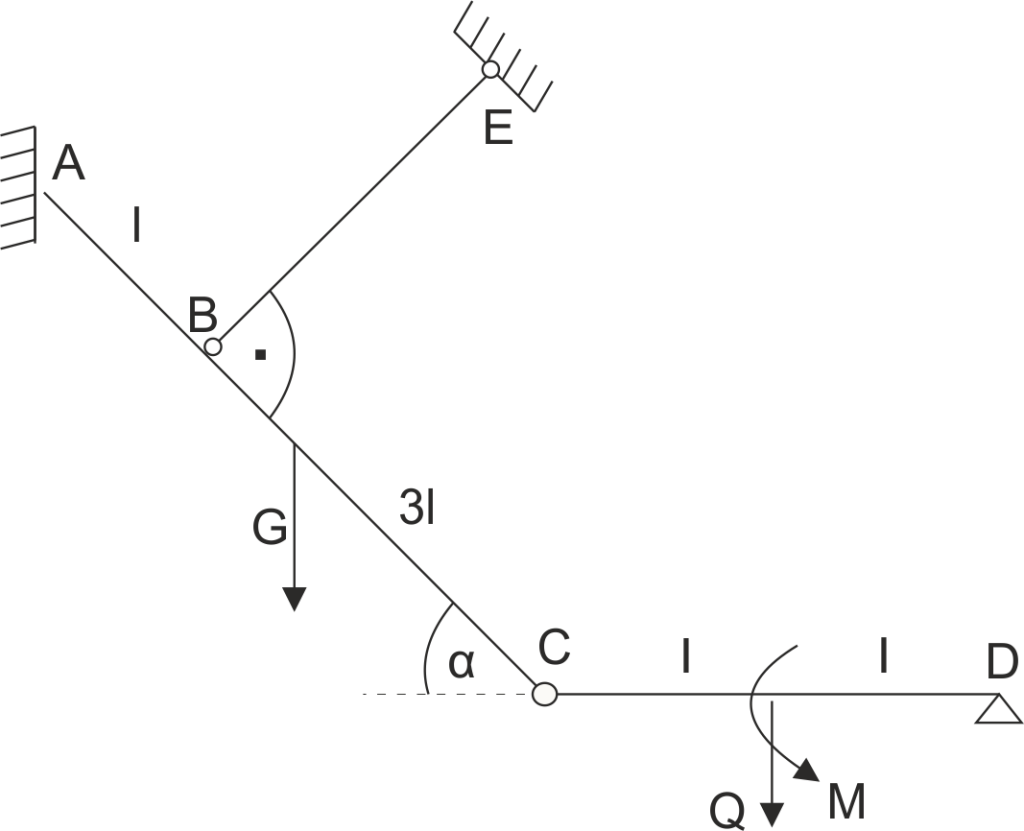
Dany jest układ belkowo-prętowy. Belka AC (o ciężarze G) i belka CD ( o ciężarze Q) połączone są przegubowo. Belka AC podparta jest swobodnie w punkcie A, dodatkowo podwieszona jest na cięgnie BE. Obliczyć reakcje podporowe, oraz reakcje w przegubie.
Przykład 14
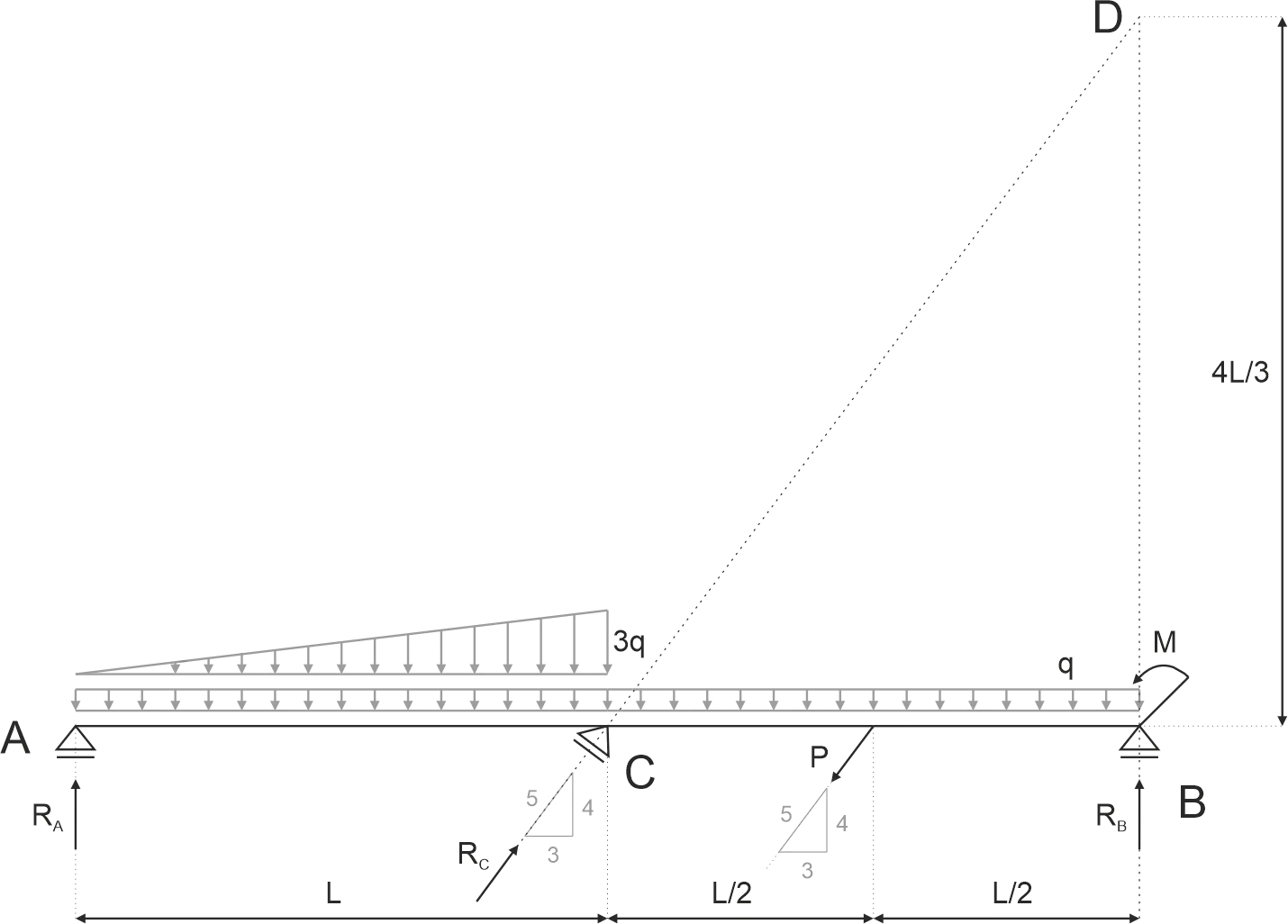
Wyznacz wartosci reakcji \(R_A\), \(R_B\) i \(R_C\) w belce przedstawionej na rysunku. Przyjmij wartość momentu \(M=400 kNm\), wartość siły \(P=100 kN\), wartość obciążenia rozłożonego \(q=10 kN/m\), długość \(L=10 m\).