Lista zadań
Przykład 1
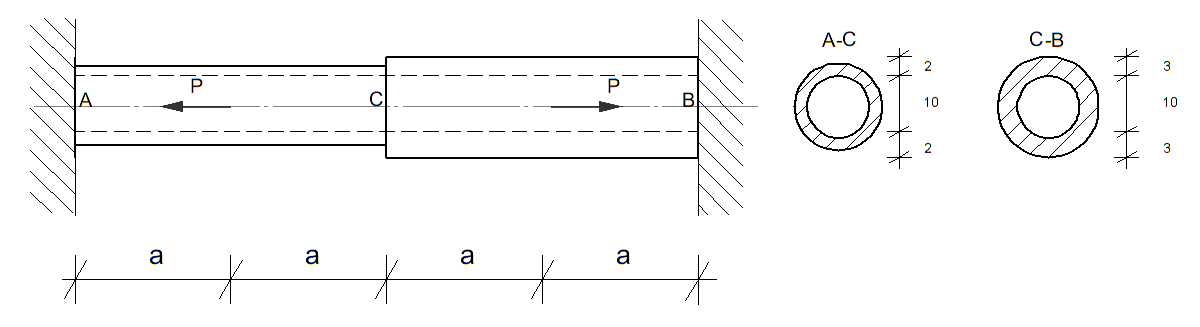
Wyznaczyć taką wartość obciążenia \( P = P_s \), przy którym największe naprężenie w pręcie osiągnie wartość równą \( R_{pl} \).
Następnie, posługując się metodą stanów granicznych nośności, wyznaczyć taką wartość obciążenia \( P = P_n \), przy którym pręt osiągnie stan graniczny nośności.
Przyjąć \( a = 0.5\,\mathrm{m} \), \( R_{pl} = 240\,\mathrm{MPa} \), \( E = 205\,\mathrm{GPa} \), a wymiary przekroju pręta podane na rysunku. Wynik podać w kN.
Wyznaczyć ponadto stosunek \( \frac{P_n}{P_s} \).
Przykład 2
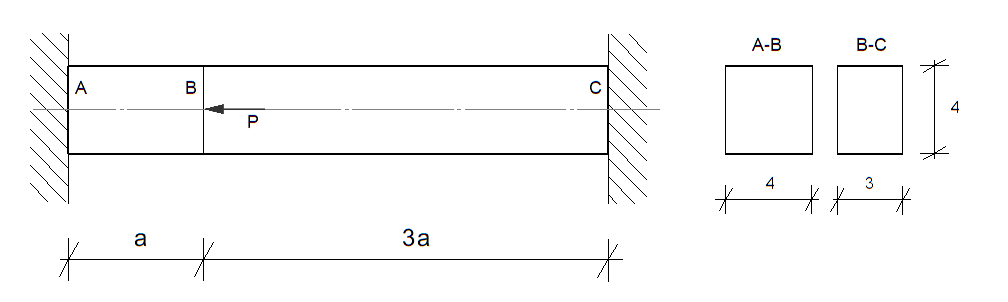
Wyznaczyć taką wartość obciążenia \( P = P_s \), przy którym największe naprężenie w pręcie osiągnie wartość równą \( R_{pl} \).
Następnie, posługując się metodą stanów granicznych nośności, wyznaczyć taką wartość obciążenia \( P = P_n \), przy którym pręt osiągnie stan graniczny nośności.
Przyjąć \( a = 1\,\mathrm{m} \), \( R_{pl} = 240\,\mathrm{MPa} \), \( E = 205\,\mathrm{GPa} \), a wymiary przekroju pręta podane na rysunku. Wynik podać w kN.
Wyznaczyć ponadto stosunek \( \frac{P_n}{P_s} \).
Przykład 3
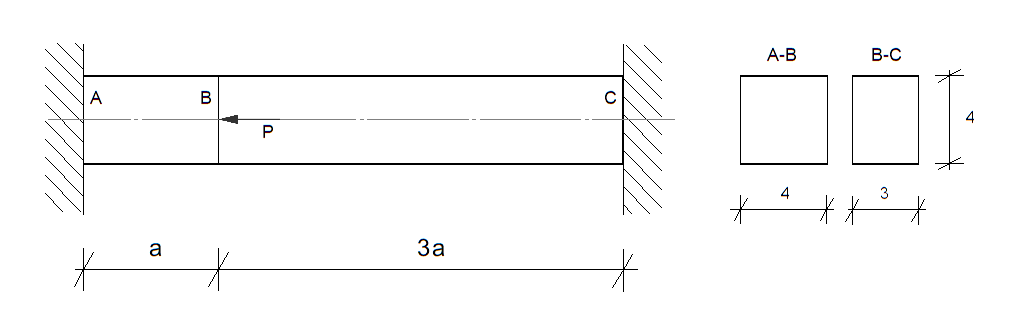
Wyznaczyć taką wartość obciążenia \( P = P_s \), przy którym największe naprężenie w pręcie osiągnie wartość równą \( R_{pl} \).
Następnie, posługując się metodą stanów granicznych nośności, wyznaczyć taką wartość obciążenia \( P = P_n \), przy którym pręt osiągnie stan graniczny nośności.
Przyjąć \( a = 1\,\mathrm{m} \), \( R_{pl} = 240\,\mathrm{MPa} \), \( E = 205\,\mathrm{GPa} \), a wymiary przekroju pręta podane na rysunku. Wynik podać w kN.
Wyznaczyć ponadto stosunek \( \frac{P_n}{P_s} \).
Przykład 4
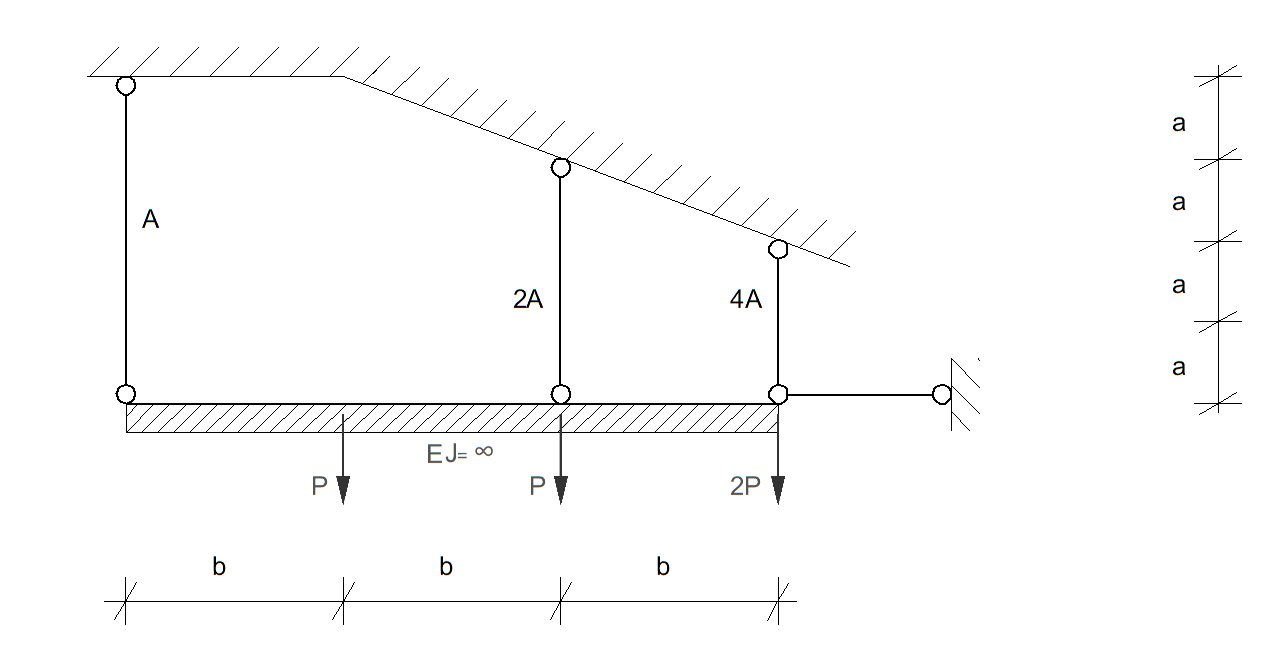
Stosując metodę stanów granicznych (podejście statyczne), wyznaczyć wartość siły \( P = P_n \), przy której zostanie wyczerpana nośność przedstawionego obok układu prętowego.
Po wyznaczeniu siły \( P_n \), stosując podejście kinematyczne, wykazać, że podane rozwiązanie jest ścisłe.
Przyjąć: \( a = 1 \ \text{m}, \quad b = 2 \ \text{m}, \quad A = 5 \ \text{cm}^2, \quad R_{pl} = 240 \ \text{MPa} \).