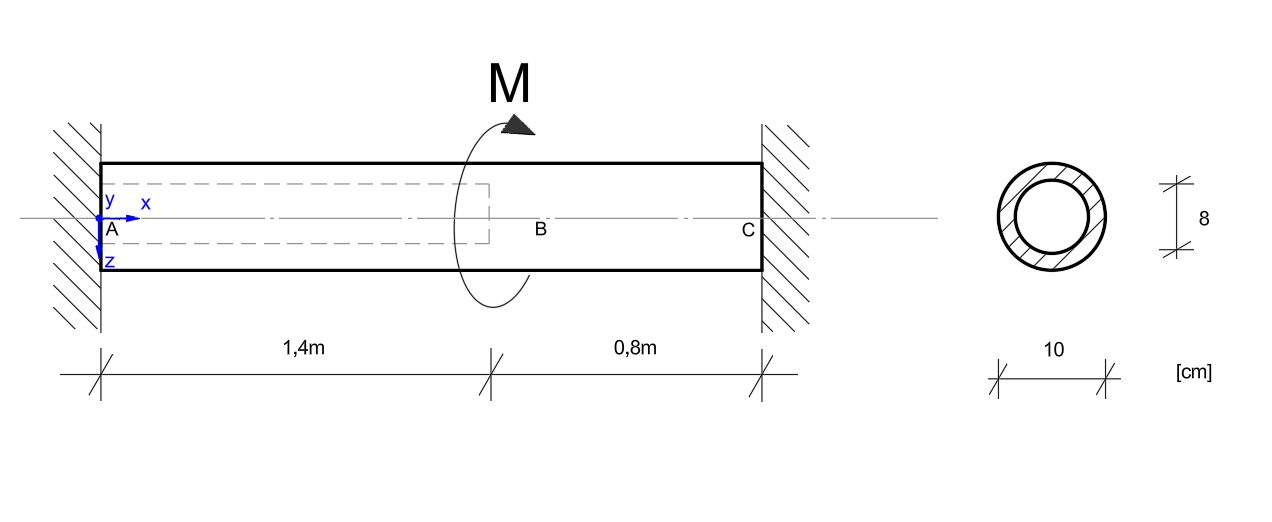
Posługując się metodą stanów granicznych nośności wyznaczyć taką wartość obciążenia \( M = M_n \), przy którym pręt przedstawiony niżej na rysunku osiągnie stan graniczny nośności. Przyjąć hipotezę Hubera i \( R_{pl} = 220\ \mathrm{MPa} \) (przy rozciąganiu). Na odcinku AB pręt ma przekrój pierścieniowy, a na BC kołowy.

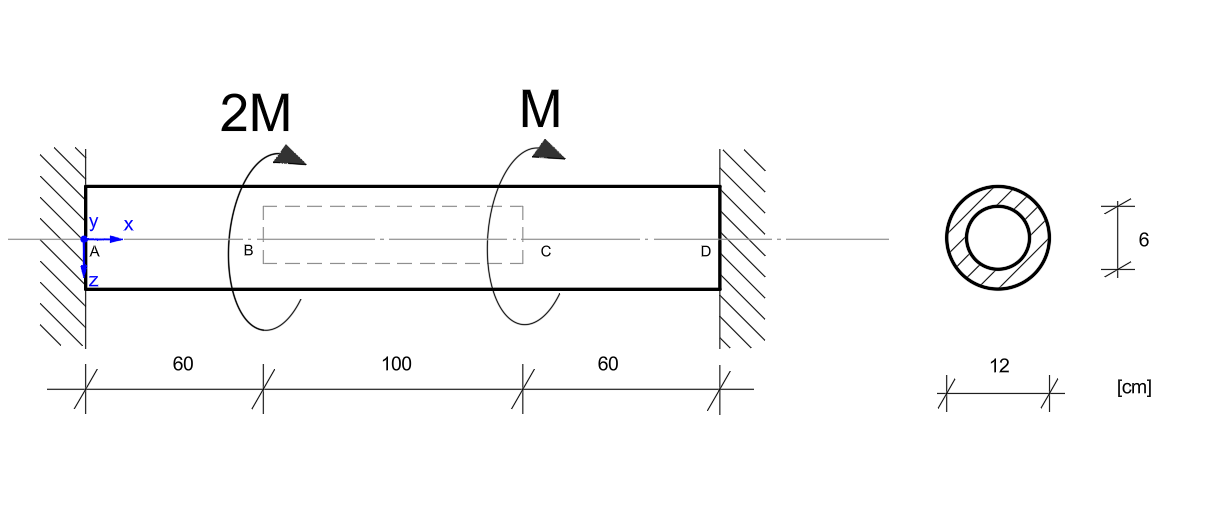
Posługując się metodą stanów granicznych nośności, wyznaczyć taką wartość obciążenia \( M = M_n \), przy którym pręt przedstawiony niżej na rysunku osiągnie stan graniczny nośności. Przyjąć hipotezę Hubera i \( R_{pl} = 220 \, \text{MPa} \) (przy rozciąganiu). Na odcinku BC pręt ma przekrój pierścieniowy, a na pozostałych odcinkach – kołowy.

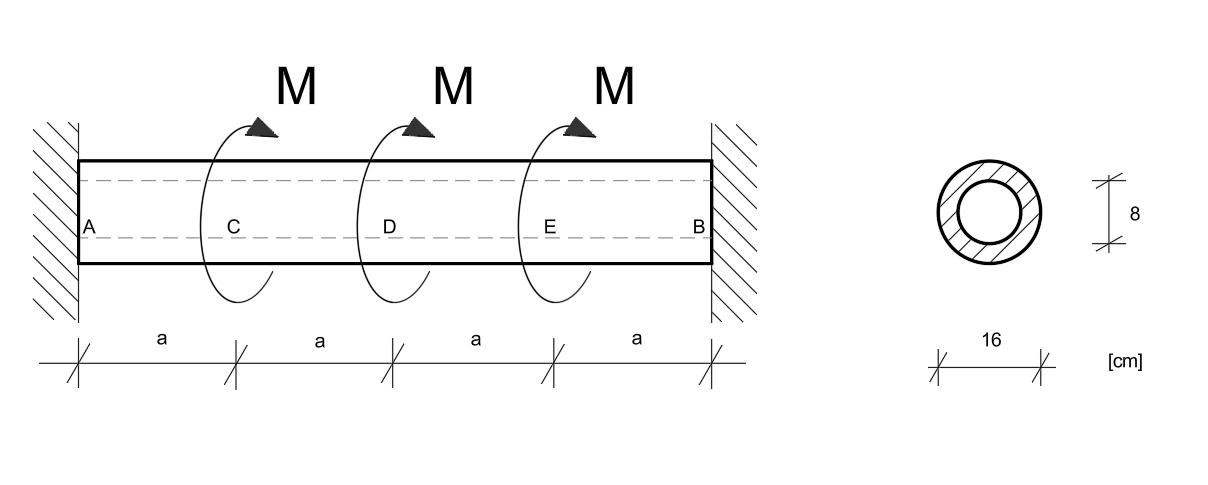
Wyznaczyć taką wartość momentu \( M = M_n \), przy którym niżej przedstawiony pręt skręcany osiągnie stan graniczny nośności. Następnie wyznaczyć taką wartość momentu \( M = M_s \), przy którym uplastycznieniu ulegną tylko włókna skrajne w najbardziej obciążonym przekroju. Wyznaczyć stosunek \( \frac{M_n}{M_s} \). W obliczeniach przyjąć \( a = 80 \,\text{cm} \) oraz hipotezę Coulomba-Treski i granicę plastyczności przy rozciąganiu \( R_{pl} = 260 \,\text{MPa} \).

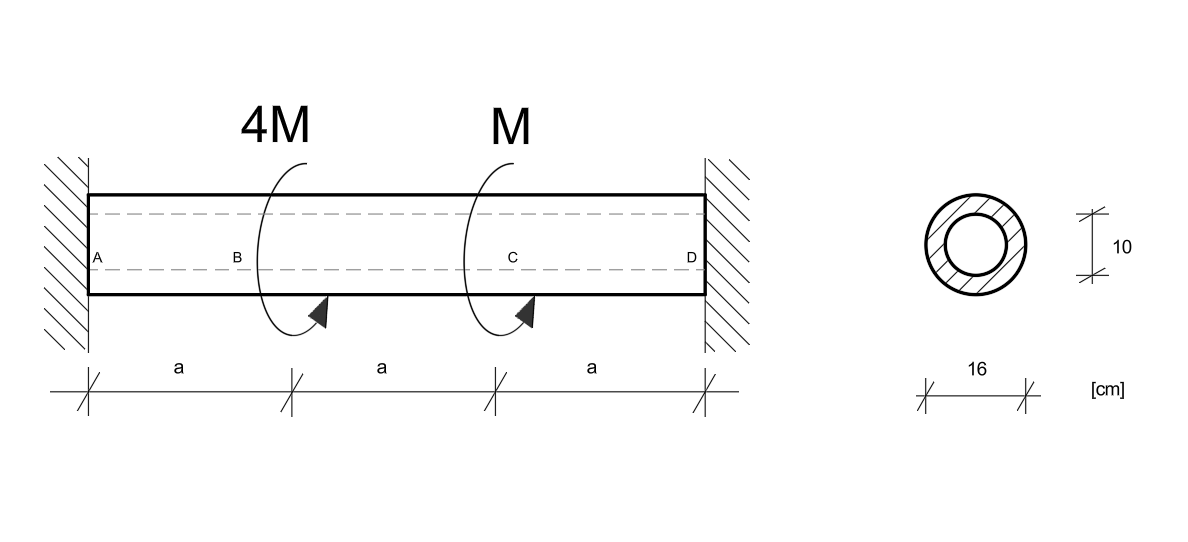
Wyznaczyć taką wartość momentu \( M = M_n \), przy którym niżej przedstawiony pręt skręcany osiągnie stan graniczny nośności. Następnie wyznaczyć taką wartość momentu \( M = M_s \), przy którym uplastycznieniu ulegną tylko włókna skrajne w najbardziej obciążonym przekroju. Wyznaczyć stosunek \( \frac{M_n}{M_s} \). W obliczeniach przyjąć \( a = 80 \,\text{cm} \) oraz hipotezę Coulomba-Treski i granicę plastyczności przy rozciąganiu \( R_p = 260 \,\text{MPa} \).

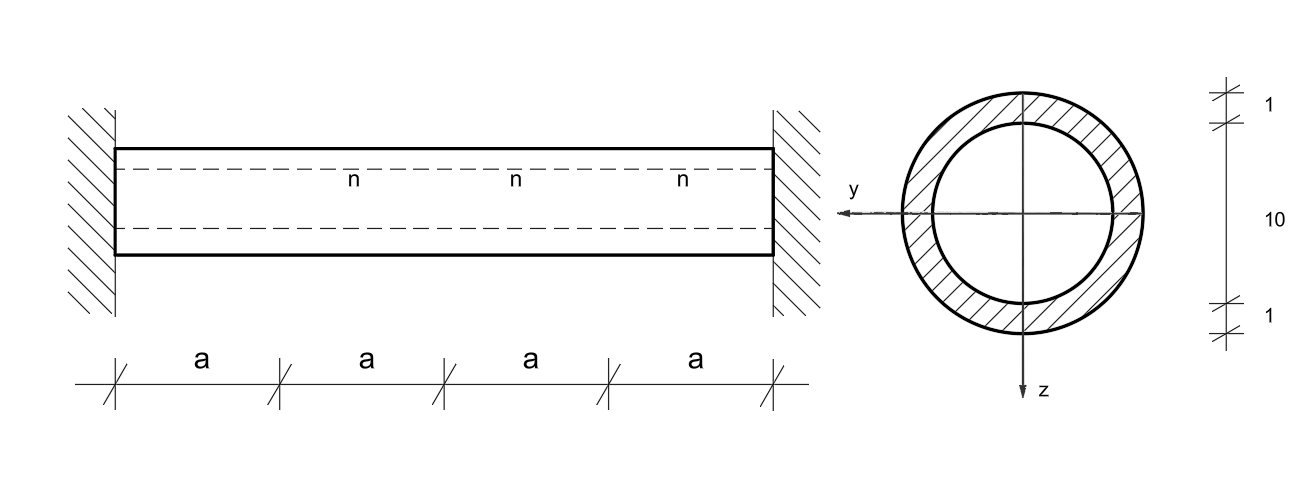
Przyjmując hipotezę Hubera znaleźć nośności sprężystą i plastyczną. Sporządzić wykres momentów skręcających w stanie granicznym n. Określić, ile razy nośność plastyczna jest większa od sprężystej.