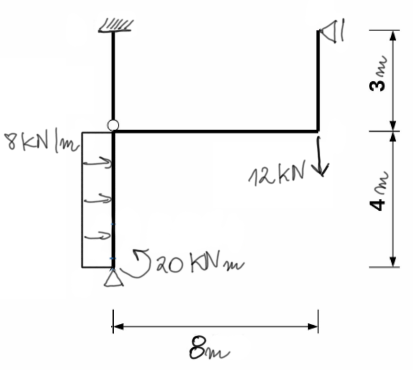
Solución
Licamos el grado de indeterminación estática SSN
y seleccionamos el sistema básico del método de fuerzas UPMS.
específico, ya que tenemos dos reacciones verticales a lo largo de la barra AC.
Por lo tanto, es una indeterminación axial, que no resolveremos con el método de fuerzas,
sino que la resolveremos en la etapa de cálculo de las fuerzas normales a partir de la condición geométrica.
A pesar de eso, resolveremos este sistema como indeterminado doble, sin embargo, como veremos en un momento
uno de los estados unitarios resultará ser cero, así que es como si estuviéramos calculando el sistema con SSN=1.




Si tienes problemas para dibujar los gráficos de momentos, te animamos a que consultes este curso en video (HAGA CLIC)
\begin{aligned} & \delta_{11}=\frac{1}{\mathrm{EI}} \cdot(0) \\ & \delta_{22}=\frac{1}{\mathrm{EI}} \cdot\left(\frac{1}{3} \cdot \frac{12}{7} \cdot \frac{12}{7} \cdot 4+\frac{12}{7} \cdot \frac{12}{7} \cdot 8+\frac{1}{3} \cdot \frac{12}{7} \cdot \frac{12}{7} \cdot 3+\frac{1}{3} \cdot 3 \cdot 3 \cdot 3\right)=\frac{1929}{49} \frac{1}{\mathrm{EI}} \\ & \delta_{12}=\frac{1}{\mathrm{EI}} \cdot(0) \quad \delta_{21}=\delta_{12} \\ & \Delta_{1P}=\frac{1}{\mathrm{EI}} \cdot(0) \\ \end{aligned} \( \Delta_{2P}= \) 
\begin{aligned} & \Delta_{2 P}=\frac{1}{\mathrm{EI}} \cdot\left(\frac{1}{3} \cdot \frac{12}{7} \cdot 4 \cdot 36+\frac{1}{6} \cdot \frac{12}{7} \cdot 4 \cdot 20-\frac{1}{3} \cdot \frac{12}{7} \cdot 4 \cdot 16+\frac{1}{2} \cdot \frac{12}{7} \cdot 8 \cdot 36-\frac{1}{2} \cdot \frac{12}{7} \cdot 8 \cdot 60-\frac{1}{3} \cdot \frac{12}{7} \cdot 3 \cdot 60\right) \\ & \Delta_{2 P}=-\frac{1392}{7} \frac{1}{\mathrm{EI}} \end{aligned}



La elongación de la barra BC es igual a la contracción de la barra AB - y esa es la condición geométrica.
Recordemos la fórmula para la elongación/contracción de una barra: \( \Delta_L = \frac{N\cdot L}{EA} \)

Verificación cinemática \( \delta_i=\int \frac{Most \cdot \overline{M_i}}{EI} d S=0 \)

\begin{aligned} & \delta_2=\frac{1}{\mathrm{EI}} \cdot\left(\begin{array}{l} \frac{1}{3} \cdot 3 \cdot 3 \cdot 15 \cdot 15+\frac{1}{3} \cdot \frac{12}{7} \cdot 4 \cdot 44.657+\frac{1}{6} \cdot \frac{12}{7} \cdot 4 \cdot 20-\frac{1}{3} \cdot \frac{12}{7} \cdot 4 \cdot 16+\frac{1}{2} \cdot \frac{12}{7} \cdot 8 \cdot 44.657- \\ -\frac{1}{2} \cdot \frac{12}{7} \cdot 8 \cdot 51.343-\frac{1}{3} \cdot \frac{12}{7} \cdot 3 \cdot 51.343 \end{array}\right) \\ & \delta_2=-0.055 \frac{1}{\mathrm{EI}} \end{aligned} Boleto relativo
\( \left|\frac{\delta_2}{\Delta_{2 p}}\right|=0.027 \% \quad <1,5 \% \)
Luego, escribimos las ecuaciones de equilibrio estático y verificamos si para las reacciones leídas, todas las ecuaciones se cumplen.
 \begin{aligned}
& \Sigma \mathrm{x}=0 \\
& -5.05-17.114+8 \cdot 4-9.836=-0 \\
& \Sigma \mathrm{y}=0 \\
& 5.143+6.857-12=0 \\
& \Sigma \mathrm{M}_{\mathrm{D}}=0 \\
& -17.114 \cdot 3-5.05 \cdot 3+6.857 \cdot 8+15.15-8 \cdot 4 \cdot 2+9.836 \cdot 4+5.143 \cdot 8-20=0.002 \sim 0
\end{aligned}
\begin{aligned}
& \Sigma \mathrm{x}=0 \\
& -5.05-17.114+8 \cdot 4-9.836=-0 \\
& \Sigma \mathrm{y}=0 \\
& 5.143+6.857-12=0 \\
& \Sigma \mathrm{M}_{\mathrm{D}}=0 \\
& -17.114 \cdot 3-5.05 \cdot 3+6.857 \cdot 8+15.15-8 \cdot 4 \cdot 2+9.836 \cdot 4+5.143 \cdot 8-20=0.002 \sim 0
\end{aligned}
y seleccionamos el sistema básico del método de fuerzas UPMS.
SSN=6-3-1=2
En términos de grado de indeterminación estática, este ejemplo es un pocoespecífico, ya que tenemos dos reacciones verticales a lo largo de la barra AC.
Por lo tanto, es una indeterminación axial, que no resolveremos con el método de fuerzas,
sino que la resolveremos en la etapa de cálculo de las fuerzas normales a partir de la condición geométrica.
A pesar de eso, resolveremos este sistema como indeterminado doble, sin embargo, como veremos en un momento
uno de los estados unitarios resultará ser cero, así que es como si estuviéramos calculando el sistema con SSN=1.
UPMS

Dibujamos los gráficos unitarios y el gráfico de carga externa.
Estado X1=1

Estado X2=1

Estado P

Si tienes problemas para dibujar los gráficos de momentos, te animamos a que consultes este curso en video (HAGA CLIC)
Calculamos los coeficientes y términos libres de la ecuación canónica del método de fuerzas
Más información sobre la integración la encontrarás en nuestra Introducción teórica sobre este tema\begin{aligned} & \delta_{11}=\frac{1}{\mathrm{EI}} \cdot(0) \\ & \delta_{22}=\frac{1}{\mathrm{EI}} \cdot\left(\frac{1}{3} \cdot \frac{12}{7} \cdot \frac{12}{7} \cdot 4+\frac{12}{7} \cdot \frac{12}{7} \cdot 8+\frac{1}{3} \cdot \frac{12}{7} \cdot \frac{12}{7} \cdot 3+\frac{1}{3} \cdot 3 \cdot 3 \cdot 3\right)=\frac{1929}{49} \frac{1}{\mathrm{EI}} \\ & \delta_{12}=\frac{1}{\mathrm{EI}} \cdot(0) \quad \delta_{21}=\delta_{12} \\ & \Delta_{1P}=\frac{1}{\mathrm{EI}} \cdot(0) \\ \end{aligned}

\begin{aligned} & \Delta_{2 P}=\frac{1}{\mathrm{EI}} \cdot\left(\frac{1}{3} \cdot \frac{12}{7} \cdot 4 \cdot 36+\frac{1}{6} \cdot \frac{12}{7} \cdot 4 \cdot 20-\frac{1}{3} \cdot \frac{12}{7} \cdot 4 \cdot 16+\frac{1}{2} \cdot \frac{12}{7} \cdot 8 \cdot 36-\frac{1}{2} \cdot \frac{12}{7} \cdot 8 \cdot 60-\frac{1}{3} \cdot \frac{12}{7} \cdot 3 \cdot 60\right) \\ & \Delta_{2 P}=-\frac{1392}{7} \frac{1}{\mathrm{EI}} \end{aligned}
Resolvemos el sistema de ecuaciones canónicas y calculamos X1 y X2.
\begin{aligned} &\delta_{11}\cdot{x_1}+\delta_{12}\cdot{x_2}+\delta_{1P}=0 \\ &\delta_{21}\cdot{x_1}+\delta_{22}\cdot{x_2}+\delta_{2P}=0 \\ \end{aligned} \begin{aligned} & \left\{\begin{array}{l} 0 \cdot x_1+0 \cdot x_2+0=0 \\ 0 \cdot x_1+\frac{1929}{49 EI} \cdot x_2-\frac{1392}{7 EI}=0 \end{array}\right. \\ & \left\{\begin{array}{l} 0=0 \\ x_2=5,05 \mathrm{kN} \end{array}\right. \end{aligned}Calculamos el momento final a partir de la fórmula de superposición
\begin{aligned} &M_{OST}=M_P+M_1\cdot{X_1}+M_2\cdot{X_2}\\ \end{aligned} Sumamos los gráficos
Gráfico del Puente

Cálculos para el gráfico de fuerzas cortantes
 | \begin{aligned}
& \Sigma M_A=0 \\
& -20+44,657+8 \cdot 4 \cdot 2+ \\
& +Q_B \cdot 4=0 \\
& Q_B=-22,164 \mathrm{kN} \\
& \Sigma x=0 \\
& Q_B+8 \cdot 4-Q_A=0 \\
& Q_A=9,836 \mathrm{kN}
\end{aligned} Extremo en el gráfico de momentos \begin{aligned} \frac{9,836}{x} & =\frac{22,164}{4-x} \\ x & =1,23 \mathrm{~m} \end{aligned} \begin{aligned} \text { Mex }=-20+Q_A \cdot x-8 \cdot \frac{x^2}{2}=-13,953 \mathrm{kNm} \end{aligned} |
 \begin{aligned} & \Sigma M_B=0 \\ & Q_C \cdot 3+15,15=0 \\ & Q_C=-5,05 \mathrm{kN} \\ & \Sigma X=0 \\ & Q_B=Q_C \end{aligned} |  \begin{aligned} & \Sigma M_B=0 \\ & -44,657-51,343+ \\ & +Q_D \cdot 8=0 \\ & Q_D=12 \mathrm{kN} \\ & \Sigma y=0 \\ & Q_B=Q_D \end{aligned} |  \begin{aligned} & \Sigma M_D=0 \\ & 51,343+Q_E \cdot 3=0 \\ & Q_E=-17,114 \mathrm{kN} \\ & \Sigma x=0 \\ & Q_D=Q_E \end{aligned} |
Gráfico de fuerzas cortantes

Cálculos para el gráfico de fuerzas normales
 \begin{aligned} & \Sigma x=0 \\ & -5,05+22,164+ \\ & +N_{B D}=0 \\ & N_{B D}=-17,114 \mathrm{kN} \\ & \sum y=0 \\ & N_{B C}-12-N_{A B}=0 \\ & * N_{B C}=12+N_{A B} \\ \end{aligned} aquí tenemos esa indeterminación axial de la que hablamos al principio | Nodo D \begin{gathered} \sum x=0(\text { spr.) } \\ -N_{B D}-17,114=0 \\ 0=0 \\ \Sigma y=0 \\ 12+N_{D E}-12=0 \\ N_{D E}=0 \mathrm{kN} \end{gathered} |
Solución de la indeterminación axial (condición geométrica)
La fuerza cortante de 12kN y su dirección nos indican hacia dónde se moverá el nodo B, y por lo tanto, qué barra se estirará y cuál se comprimirá.La elongación de la barra BC es igual a la contracción de la barra AB - y esa es la condición geométrica.
Recordemos la fórmula para la elongación/contracción de una barra: \( \Delta_L = \frac{N\cdot L}{EA} \)
 | \begin{aligned} & \Delta L_{A B}=\Delta L_{B C} \\ & \frac{-N_{A B} \cdot 4}{E A}=\frac{N_{B C} \cdot 3}{E A} \\ & -4 N_{A B}=3 N_{B C} \\ & N_{A B}=-0,75 N_{B C} \\ & * N_{B C}=12-0,75 N_{B C} \\ & \left\{\begin{array}{l} N_{B C}=6,857 \mathrm{kN} \\ N_{A B}=-5,143 \mathrm{kN} \end{array}\right. \\ & \end{aligned} |
Gráfico final de fuerzas normales

Verificación cinemática \( \delta_i=\int \frac{Most \cdot \overline{M_i}}{EI} d S=0 \)

\begin{aligned} & \delta_2=\frac{1}{\mathrm{EI}} \cdot\left(\begin{array}{l} \frac{1}{3} \cdot 3 \cdot 3 \cdot 15 \cdot 15+\frac{1}{3} \cdot \frac{12}{7} \cdot 4 \cdot 44.657+\frac{1}{6} \cdot \frac{12}{7} \cdot 4 \cdot 20-\frac{1}{3} \cdot \frac{12}{7} \cdot 4 \cdot 16+\frac{1}{2} \cdot \frac{12}{7} \cdot 8 \cdot 44.657- \\ -\frac{1}{2} \cdot \frac{12}{7} \cdot 8 \cdot 51.343-\frac{1}{3} \cdot \frac{12}{7} \cdot 3 \cdot 51.343 \end{array}\right) \\ & \delta_2=-0.055 \frac{1}{\mathrm{EI}} \end{aligned} Boleto relativo
\( \left|\frac{\delta_2}{\Delta_{2 p}}\right|=0.027 \% \quad <1,5 \% \)
Verificación estática
Leemos las reacciones (valores y direcciones correctas) de los gráficos de fuerzas normales, cortantes y momentos flectores.Luego, escribimos las ecuaciones de equilibrio estático y verificamos si para las reacciones leídas, todas las ecuaciones se cumplen.
 \begin{aligned}
& \Sigma \mathrm{x}=0 \\
& -5.05-17.114+8 \cdot 4-9.836=-0 \\
& \Sigma \mathrm{y}=0 \\
& 5.143+6.857-12=0 \\
& \Sigma \mathrm{M}_{\mathrm{D}}=0 \\
& -17.114 \cdot 3-5.05 \cdot 3+6.857 \cdot 8+15.15-8 \cdot 4 \cdot 2+9.836 \cdot 4+5.143 \cdot 8-20=0.002 \sim 0
\end{aligned}
\begin{aligned}
& \Sigma \mathrm{x}=0 \\
& -5.05-17.114+8 \cdot 4-9.836=-0 \\
& \Sigma \mathrm{y}=0 \\
& 5.143+6.857-12=0 \\
& \Sigma \mathrm{M}_{\mathrm{D}}=0 \\
& -17.114 \cdot 3-5.05 \cdot 3+6.857 \cdot 8+15.15-8 \cdot 4 \cdot 2+9.836 \cdot 4+5.143 \cdot 8-20=0.002 \sim 0
\end{aligned}
Si tienes preguntas, comentarios, o crees que has encontrado un error en esta solución, por favor envíanos un mensaje a kontakt@edupanda.pl.