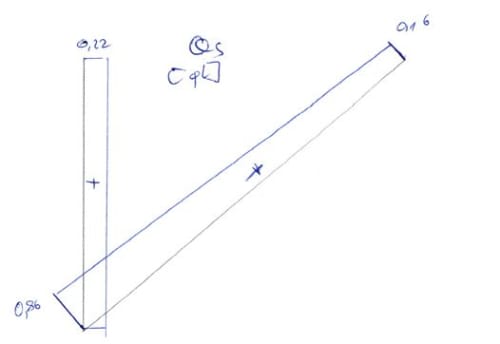
Dado que tanto el marco como la carga son simétricos, considero solo el sistema medio por simetría.

Como se puede ver para este sistema, SKN = 2

Estado \(\ varphi_1\)

De la ecuación del nodo B para los momentos

\begin{aligned} &r_{11}-\frac{3EI}{l}-\frac{2\sqrt2}{l}EI=0\\ &r_{11}=5,828\frac{EI}{l} \\ \end{aligned}

De la ecuación del nodo C para las fuerzas

\begin{aligned} &\sum{F_Y=0}\\ &-N_1\cdot sin\alpha-\frac{3}{l^2}\cdot cos\alpha = 0 \\ &N_1 = -\frac{3}{l^2} \\ \end{aligned}

\begin{aligned} &\sum{F_X=0}\\ &-\frac{3}{l^2}EI+r_{21}-\frac{3}{l^2}EI\cdot\sin{\alpha}+N_1\cdot cos\alpha=0\\ &r_{21} = 7,243\frac{EI}{l^2} \\ \end{aligned}

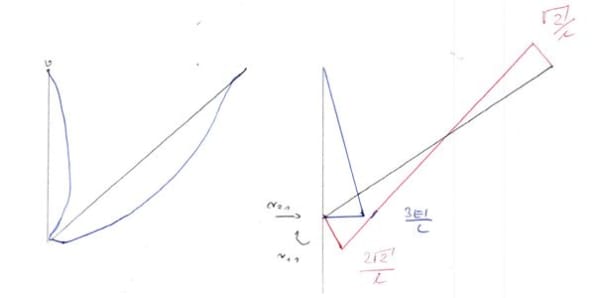
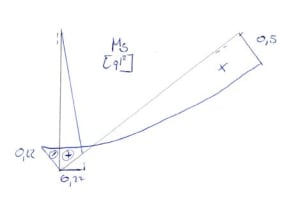
Estado \(\Delta_2\)

Observamos que del dibujo: \(sin\alpha=\frac{a}{1}\), por lo tanto \(a=\frac{1}{sin\alpha}=\sqrt2\)

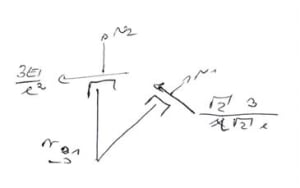
De la ecuación del nodo B para los momentos:

\begin{aligned} &r_{12}-3\frac{EI}{l^2}-4,243\frac{EI}{l^2}=0\\ &r_{12}=7,243\frac{EI}{l^2} \\ \end{aligned}

Resultado coincidente con el resultado para el estado \(\varphi_1\)

De la ecuación de los nodos B y C para las fuerzas:

\begin{aligned} &\sum{F_Y=0}\\ &-N_1\cdot sin\alpha-6\frac{EI}{l^3}=0\\ &N_1=-6\frac{EI}{l^3} \\ \end{aligned}

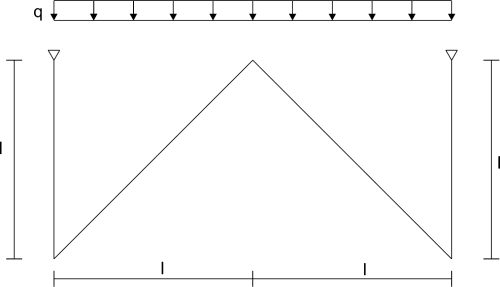
Estado P

De la ecuación del nodo B para los momentos:

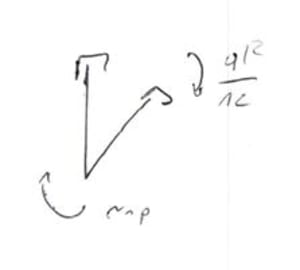\begin{aligned} &r_{1p}+\frac{ql^2}{12}=0\\ &r_{1p}=-\frac{ql^2}{12} \\ \end{aligned}

De la ecuación de los nodos B y C para las fuerzas

\begin{aligned} &\sum{F_Y=0}\\ &-N_1\cdot sin\alpha+\frac{ql\sqrt2}{4}\cdot cos\alpha=0\\ &N_1=\frac{\sqrt2}{4}ql\\ \end{aligned}

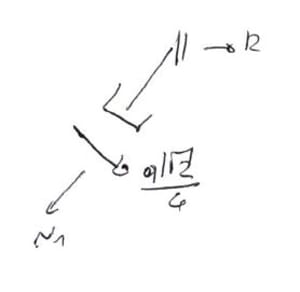
Nota - debido a la carga continua no es perpendicular al eje de la barra, tenemos:

\begin{aligned} &N_3=N_1-ql\cdot sin\alpha\\ &\sum{F_X=0}\\ &r_{2p}+N_3\cdot cos\alpha+\frac{ql\sqrt2}{4}\cdot sin\alpha=0\\ &r_{2p}=\frac{1}{2}ql\\ \end{aligned}

Sustituyendo en la ecuación canónica

\begin{aligned} &r_{11}\varphi_1+r_{12}\Delta_2+r_{1p}=0\\ &r_{21}\varphi_1+r_{22}\Delta_2+r_{2p}=0\\ &5,828\frac{EI}{l}\varphi_1+7,243\frac{EI}{l^2}\Delta_2-\frac{ql^2}{12}=0\\ &7,243\frac{EI}{l^2}\varphi_1+11,486\frac{EI}{l^3}\Delta_2+\frac{1}{2}ql=0\\ \end{aligned}

Por lo tanto:

\begin{aligned} &\varphi_1=0,316\frac{ql^3}{EI}\\ &\Delta_2=-0,243\frac{{ql}^4}{EI}\\ \end{aligned}

Por el principio de superposición

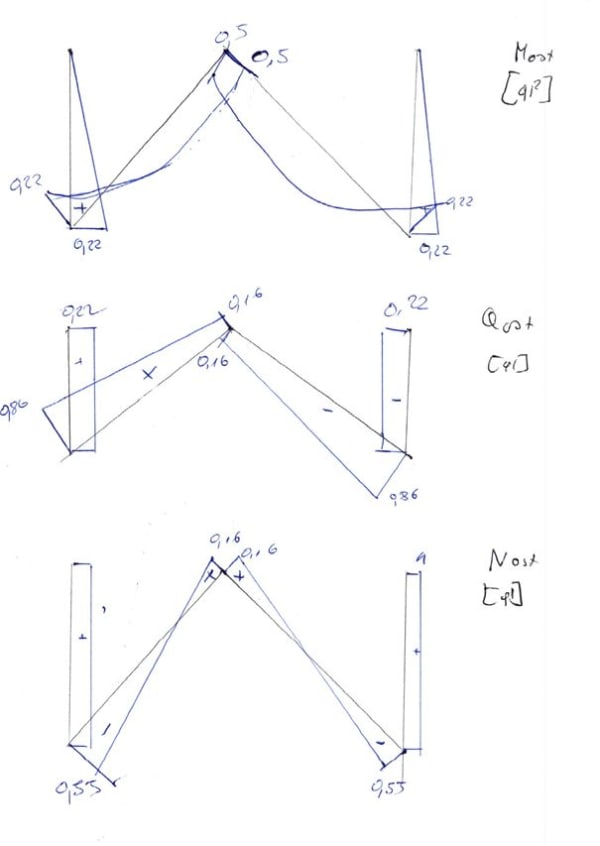
\begin{aligned} &M_{ost}=M_1\varphi_1+M_2\Delta_2+M_p\\ &M_B^A=3\frac{EI}{l^2}\cdot\Delta_2+3\frac{EI}{l^2}\cdot\varphi_1=0,22ql^2\\ &M_B^C=4,243\cdot\frac{EI}{l^2}\cdot\Delta_2+2\sqrt2\cdot\frac{EI}{l}\cdot\varphi_1-\frac{1}{12}ql^2=-0,22ql^2\\ &M_C=-4,243\cdot\frac{EI}{l^2}\cdot\Delta_2-\sqrt2\cdot\frac{EI}{l}\cdot\varphi_1-\frac{1}{12}ql^2=0,5ql^2\\ \end{aligned}

Por lo tanto, el gráfico \(M_{ost}\)

De la ecuación del elemento BC

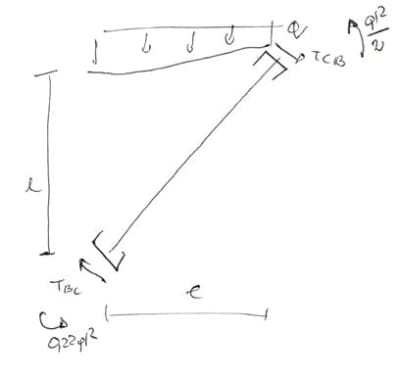\begin{aligned} &\sum{M_C=0}\\ &T_{BC}\cdot l\sqrt2-0,22ql^2-0,5ql^2-q\cdot l\cdot\frac{l}{2}=0\\ &T_{BC}=0,86ql\\ &\sum{M_B=0}\\ &-T_{CB}\cdot l\sqrt2-0,22ql^2-0,5ql^2+q\cdot l\cdot\frac{l}{2}=0\\ &T_{BC}=0.16ql\\ \end{aligned}

Por lo tanto, el gráfico \(Q_{ost}\)

De la ecuación de los nodos B y C

\begin{aligned} \sum F_y=0 &-N_{CB}\ sin\alpha+0,16ql\cdot cos\alpha=0\\ &N_{CB}=0,16ql\\ \end{aligned}

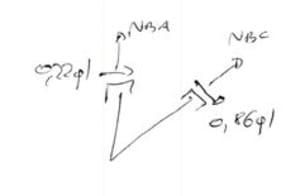
Debido a la carga continua

\begin{aligned} &N_{BC}=N_{CB}-qlsin\alpha=-0,55ql\\ &\sum{F_Y=0}\\ &N_{BA}-0,86\cdot cos\alpha+N_{BC}\cdot sin\alpha=0\\ &N_{BC}=ql\\ \end{aligned}

Por lo tanto, el gráfico \(N_{ost}\)

Por último, superponemos los gráficos del estado de simetría, recordando que para la simetría:

- Las magnitudes reflejan momentos flexionantes simétricamente (no hay cambios en los signos)

- Las magnitudes de las fuerzas cortantes se reflejan de manera antisimétrica (los signos se cambian a opuesto para la reflexión)

- Las magnitudes de las fuerzas normales se reflejan simétricamente (no hay cambios en los signos)