Solución
Fuerzas de corte
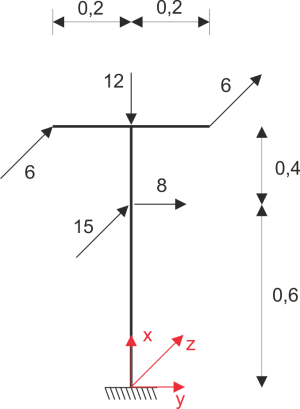 \begin{aligned}
&Q_{z}=15 k N \\
&Q_{y}=8 k N \\
&Q_{x}=N=-12 k N \\
&M_{z}=0 \\
&M_{y}=-15 \cdot 0,6=-9 k N m \\
&M_{x}=-6 \cdot 0,2-6 \cdot 0,2=-2,4 k N m
\end{aligned}
\begin{aligned}
&Q_{z}=15 k N \\
&Q_{y}=8 k N \\
&Q_{x}=N=-12 k N \\
&M_{z}=0 \\
&M_{y}=-15 \cdot 0,6=-9 k N m \\
&M_{x}=-6 \cdot 0,2-6 \cdot 0,2=-2,4 k N m
\end{aligned}
Esfuerzos cortantes
Esfuerzos generados por la fuerza \(Q_z\)
\begin{aligned} &\tau_{x z}=\frac{4}{3} \cdot \frac{Q_{z}}{A}\left(1-\frac{z^{2}}{R^{2}}\right) \\ &A=\frac{\pi \cdot 0,2^{2}}{4}=0,03 m^{2} \\ &\tau_{x z}^{A}=\frac{4}{3} \cdot \frac{15 \cdot 10^{3}}{0,03}\left(1-\frac{0,2^{2}}{0,2^{2}}\right)=0 \\ &\tau_{x y}=-\frac{4}{3} \cdot \frac{Q_{z}}{A} \frac{y z}{R^{2}} \\ &\tau_{x y}^{A}=0 \end{aligned}Esfuerzos generados por la fuerza \(Q_y\)
\begin{aligned} \tau_{x y} &=\frac{4}{3} \cdot \frac{Q_{y}}{A}\left(1-\frac{y^{2}}{R^{2}}\right) \\ \tau_{x y}^{A} &=\frac{4}{3} \cdot \frac{8 \cdot 10^{3}}{0,03}\left(1-\frac{0}{0,2^{2}}\right)=0,356 \mathrm{MPa} \\ \tau_{x z} &=-\frac{4}{3} \cdot \frac{Q_{y}}{A} \frac{y z}{R^{2}} \\ \tau_{x z}^{A} &=0 \end{aligned}Esfuerzos cortantes por torsión
\begin{aligned} &\tau_{x y}=-\frac{M_{x}}{I_{o}} z \\ &I_{o}=\frac{\pi d^{4}}{32}=1,57 \cdot 10^{-4} \mathrm{~m}^{4} \\ &\tau_{x y}^{A}=-\frac{-2,4 \cdot 10^{3}}{1,57 \cdot 10^{-4}} \cdot 0,1=1,53 M P a \\ &\tau_{x z}=\frac{M_{x}}{I_{o}} y \\ &\tau_{x z}^{A}=0 \end{aligned}Esfuerzos totales cortantes
\begin{aligned} &\tau_{x y}^{A}=1,53+0,356=1,886 \mathrm{MPa} \\ &\tau_{x z}^{A}=0 \\ &\tau^{A}=\sqrt{1,886^{2}+0^{2}}=1,886 \mathrm{MPa} \end{aligned}Esfuerzos normales
\begin{aligned} &\sigma=\frac{N}{A}+\frac{M_{y}}{I_{y}} z-\frac{M_{z}}{I_{z}} y \\ &I_{z}=I_{y}=\frac{\pi d^{4}}{64}=7,85 \cdot 10^{-5} \\ &\sigma^{A}=\frac{-12 \cdot 10^{3}}{0,03}+\frac{-9 \cdot 10^{3}}{7,85 \cdot 10^{-5}} \cdot 0,1=-11,86 \mathrm{MPa} \end{aligned}Esfuerzos reducidos
\begin{aligned} &\sigma_{\text {red }}^{H M H}=\sqrt{\sigma^{2}+3 \tau^{2}} \\ &\sigma_{\text {red }}^{H M H} A=\sqrt{(-11,86)^{2}+3 \cdot 1,886^{2}}=12,3 M P a \end{aligned}
Si tienes preguntas, comentarios, o crees que has encontrado un error en esta solución, por favor envíanos un mensaje a kontakt@edupanda.pl.
