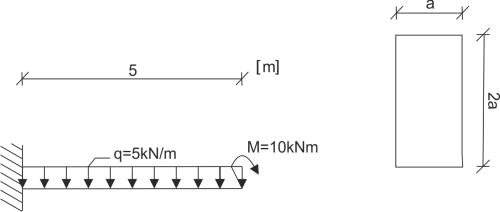
La flexion maximale se produira à l'extrémité libre de la poutre. Pour le calculer, nous utiliserons la méthode de Clebsch.

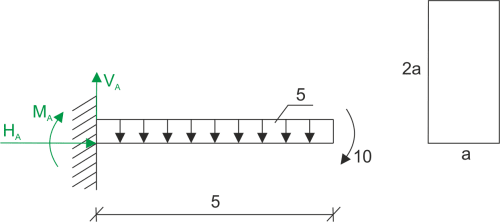\begin{aligned} &\sum{y}=0\\ &V_{A}-25=0\\ &V_{A}=25\ kN\\ &\sum{M_A}=0\\ &M_{u}+10+5\cdot 5\cdot 2,5=0\\ &M_{u}=-72,5\ kNm\\ \end{aligned}

Moment d'inertie de la section et fonction du moment pour la poutre (exprimé du côté gauche).

\begin{aligned} &I_{yc}=\frac{a\cdot (2a)^3}{12}=\frac{2}{3}a^4\\ &EI\omega''=-Mg\\ &Mg=V_{A}x+M_A\cdot x^0-\frac{1}{2}qx^2\\ &EI\omega''=-25x+72,5x^0+2,5x^2\\ &EI\omega'=-25\frac{x^2}{2}+72,5x+2,5\frac{x^3}{3}+C\\ &EI\omega=-25\frac{x^3}{6}+72,5\frac{x^2}{2}+2,5\frac{x^4}{12}+Cx+D\\ \end{aligned}

Conditions aux limites

\begin{aligned} &\omega'(0)=0\\ &C=0\\ &\omega(0)=0\\ &D=0\\ &w_{max}=\frac{w(5)}{EI}=\frac{-25\frac{5^3}{6}+72,5\cdot \frac{5^2}{2}+2,5\frac{5^4}{12}}{EI}=\frac{515,625}{EI}\\ \end{aligned}

Condition de l'énoncé du problème

\begin{aligned} &w_{max}\le w_{dop}\\ \\ &\frac{515,625\cdot 10^3}{200\cdot 10^9\cdot \frac{2}{3}a^4}\le 0,01\\ \\ &a\ge 0,14\ m\\ &a=15\ cm\\ \end{aligned}