Lista zadań
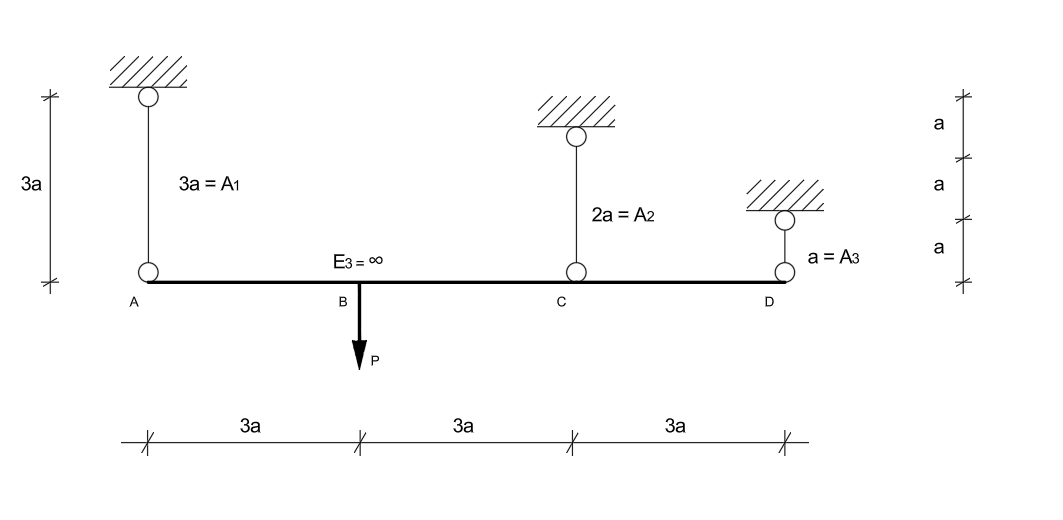
Przykład 1

Znaleźć graniczną wartość siły P. Dane: \(\sigma_P=195 MPa\)
Przykład 2

Znaleźć graniczną wartość siły P. Dane: \(\sigma_P=215 MPa\)
Przykład 3
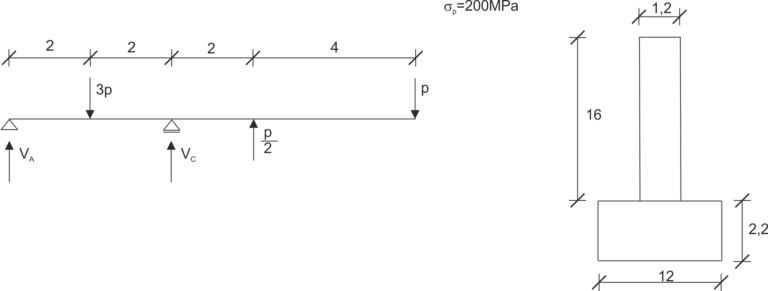
Znaleźć graniczną wartość siły P. Dane: \(\sigma_P=200 MPa\)
Przykład 4

Znaleźć graniczną wartość siły P. Dane: /(\sigma_P=210 MPa/)
Przykład 5
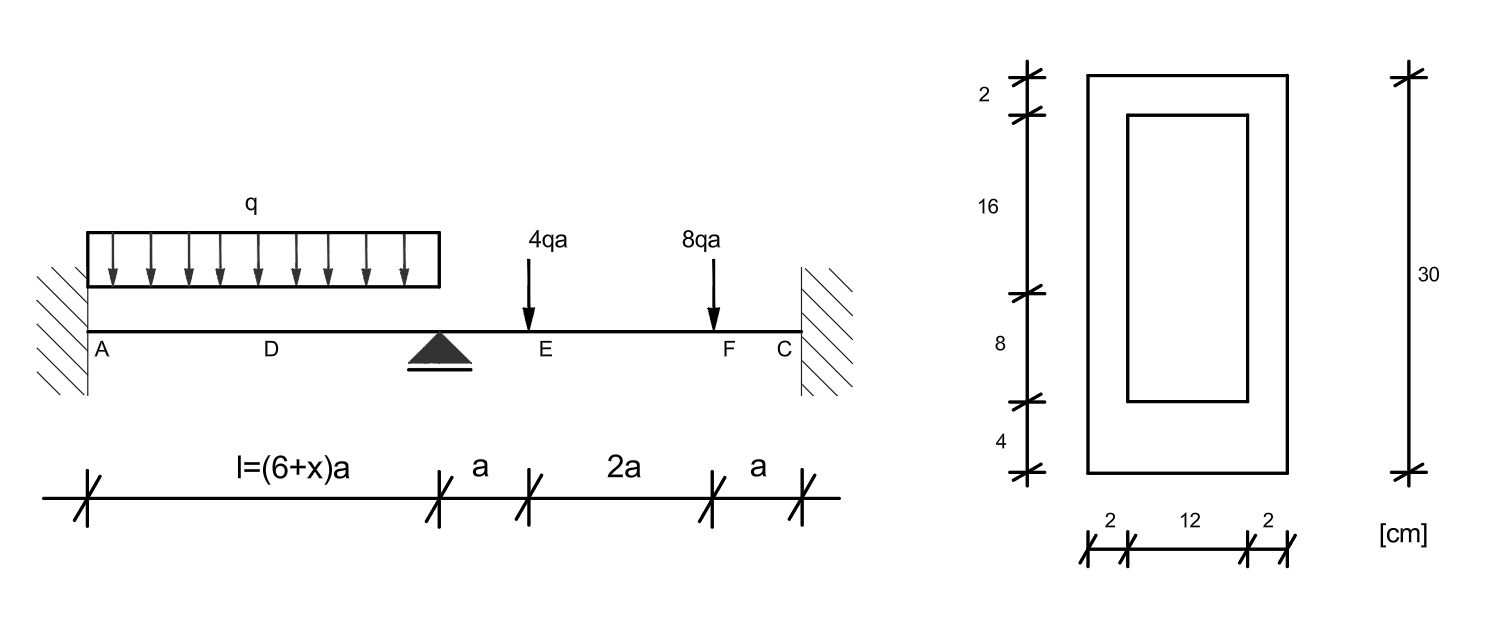
Posługując się metodą stanów granicznych nośności (podejście statyczne) wyznaczyć taką wartość obciążenia \( q = q_n \), przy którym przedstawiona niżej belka osiągnie stan graniczny nośności. Po wyznaczeniu \( q_n \), stosując podejście kinematyczne wykazać, że podane rozwiązanie jest ścisłe. Sporządzić wykresy naprężeń w przekrojach, w których został osiągnięty stan graniczny. Ostateczne wyniki podać przyjmując podane wyżej wartości \( a \) i \( R_{pl} \)
Przykład 6
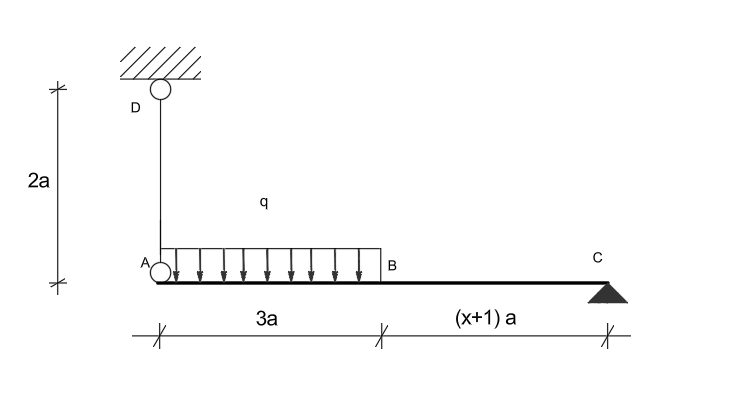
Wyznaczyć nośność graniczną podanego niżej układu prętowego. Pręt AD ma przekrój kwadratowy o boku \( 5 \, \text{cm} \), a przekrój pręta AC jest taki sam jak w zadaniu 1. W obliczeniach przyjąć wyznaczone wcześniej wartości \( a \) i \( R_{\text{pl}} \).
Przykład 8
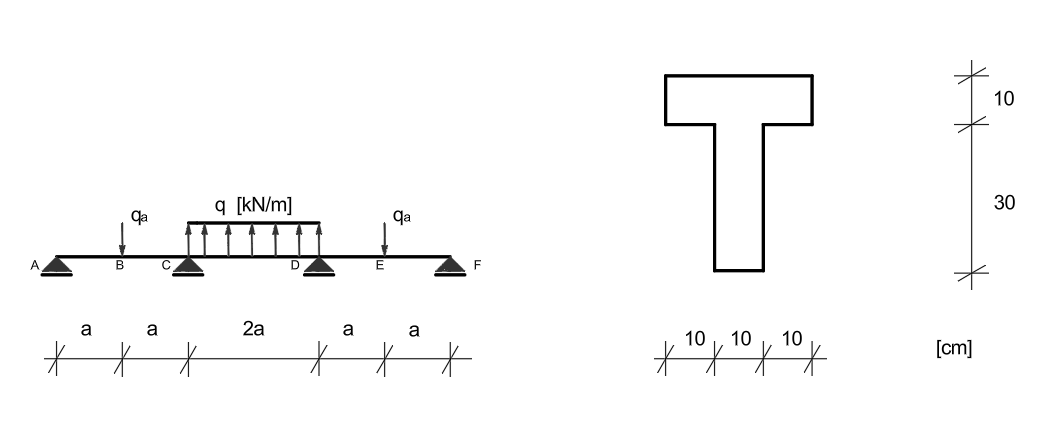
Korzystając z metody kinematycznej znaleźć nośność graniczną. Wykazać kompletność rozwiązania.
Przykład 9
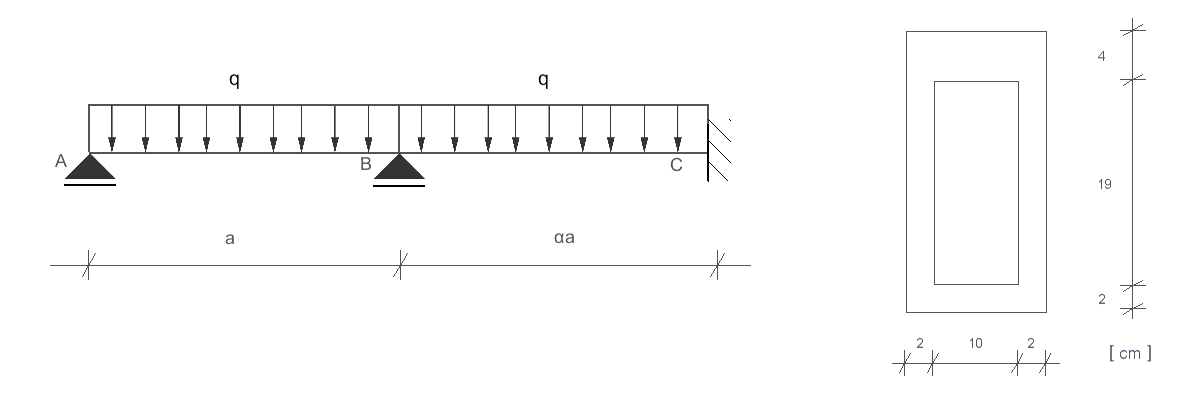
Posługując się metodą stanów granicznych nośności (podejście statyczne), wyznaczyć taką wartość współczynnika \( \alpha \), aby belka podana na rysunku osiągnęła stan graniczny nośności jednocześnie w obu przęsłach.
Następnie, przyjmując wyznaczoną wartość \( \alpha \), korzystając z podejścia kinematycznego, wyznaczyć nośność graniczną \( q_n \) i wykazać, że przy wyznaczonej wartości \( q_n \) nastąpi jednoczesne osiągnięcie stanu granicznego w obu przęsłach.
W obliczeniach przyjąć: \( a = 5 \ \text{m}, \quad R_{pl} = 240 \ \text{MPa} \).
Przykład 9

Posługując się metodą stanów granicznych nośności wyznaczyć taką wartość obciążenia \( q = q_n \), przy którym belka przedstawiona niżej na rysunku osiągnie stan graniczny nośności. Zadanie rozwiązać metodą statyczną, a następnie sprawdzić metodą kinematyczną czy rozwiązanie jest kompletne. Przyjąć \( a = 1\,\text{m} \) i \( R_e = 250\,\text{MPa} \).
Przykład 10
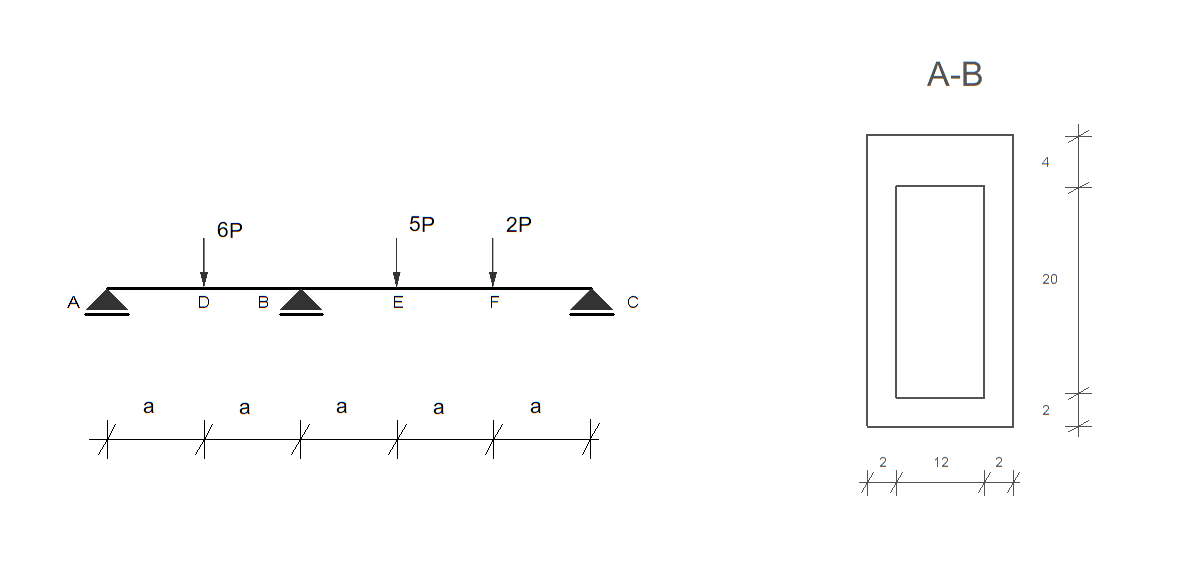
Posługując się metodą stanów granicznych nośności wyznaczyć taką wartość obciążenia \( P = P_n \), przy którym belka przedstawiona niżej na rysunku osiągnie stan graniczny nośności. Zadanie rozwiązać metodą statyczną a następnie sprawdzić metodą kinematyczną czy rozwiązanie jest kompletne. Przyjąć \( a = 1\,\text{m} \) i \( R_e = 240\,\text{MPa} \).
Przykład 11
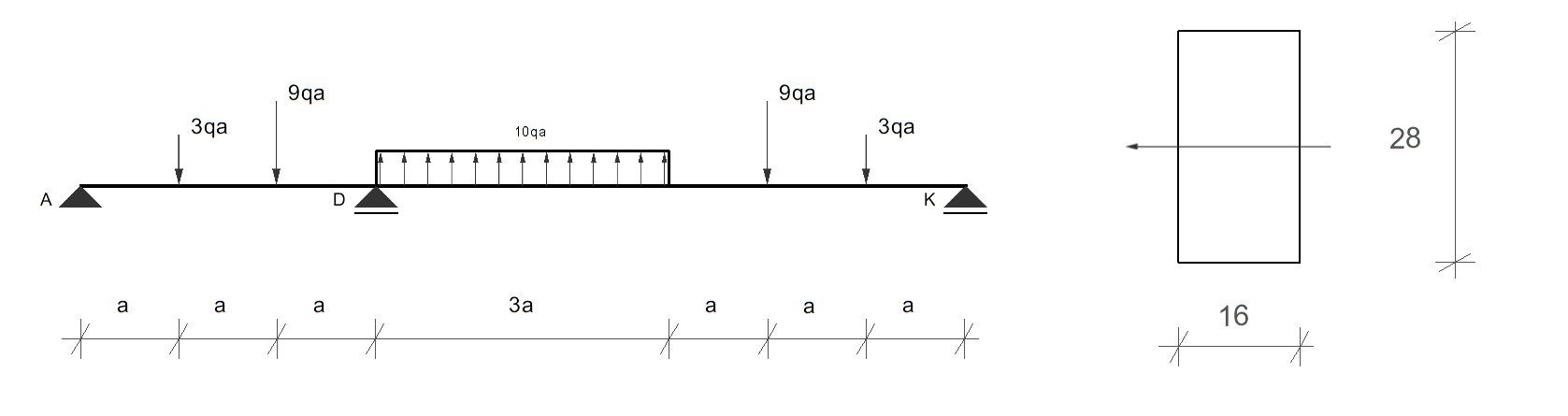
Posługując się metodą stanów granicznych wyznaczyć taką wartość obciążenia \( q = q_n \), przy którym dana belka osiągnie stan graniczny nośności. Zadanie rozwiązać metodą statyczną, a następnie sprawdzić ścisłość rozwiązania metodą kinematyczną. Dane: a = 1m, Re = 240MPa
Przykład 12
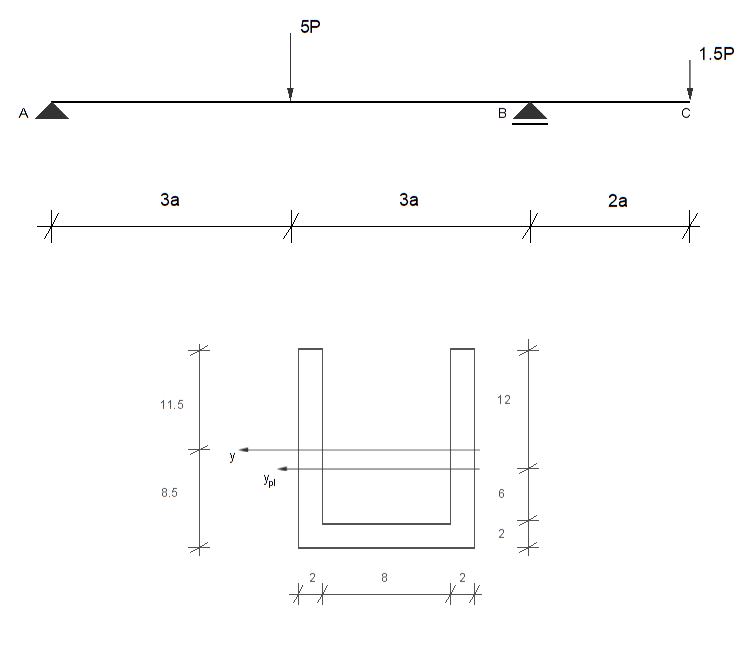
Wyznaczyć taką wartość obciążenia \( P = P_n \), przy którym dana belka zginana osiągnie stan graniczny nośności. Następnie wyznaczyć taką wartość obciążenia \( P = P_s \), przy którym uplastycznieniu ulegną tylko skrajne włókna w najbardziej obciążonym przekroju. Wyznaczyć stosunek \( \frac{P_n}{P_s} \).
Dane: \( a = 1\,\text{m}, \quad R_e = 250\,\text{MPa} \)
Przykład 13
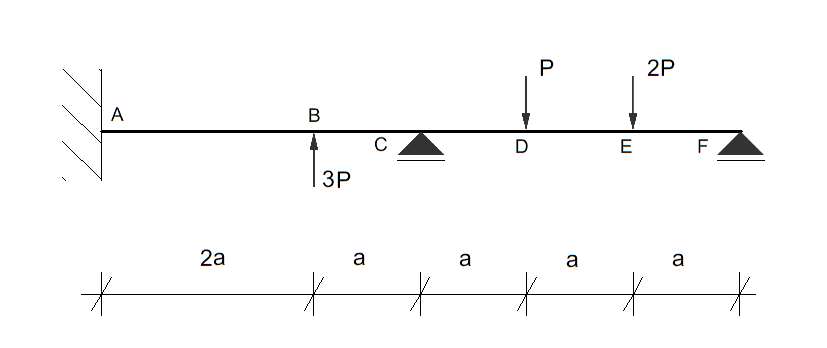
Posługując się metodą stanów granicznych nośności, wyznaczyć taką wartość obciążenia \( P = P_n \), przy której przedstawiona obok belka osiągnie stan graniczny nośności.
Sprawdzić, czy otrzymane rozwiązanie jest kompletne (ścisłe).
W obliczeniach przyjąć jako dane parametry: \( a \), \( W_{pl} \) i \( R_{pl} \).