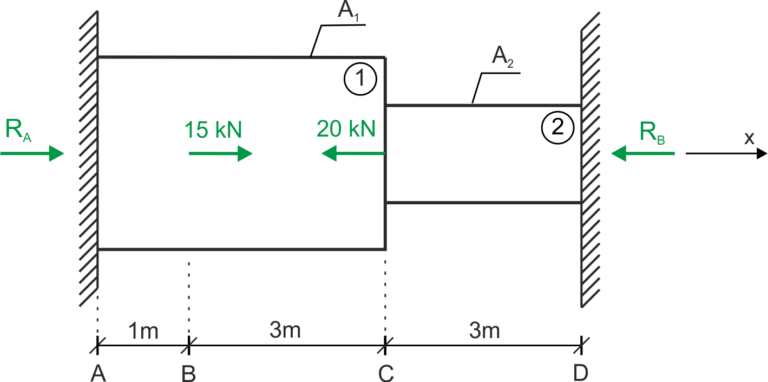
Dwustopniowy pręt został trwale utwierdzony końcem A, końcem D i obciążony siłami jak na rysunku. Obliczyć reakcję w utwierdzeniach, wskazać w której części pręta powstają największe naprężenia. Dane: \( A_1=2\cdot A_2, 2\cdot E_1=E_2 \)

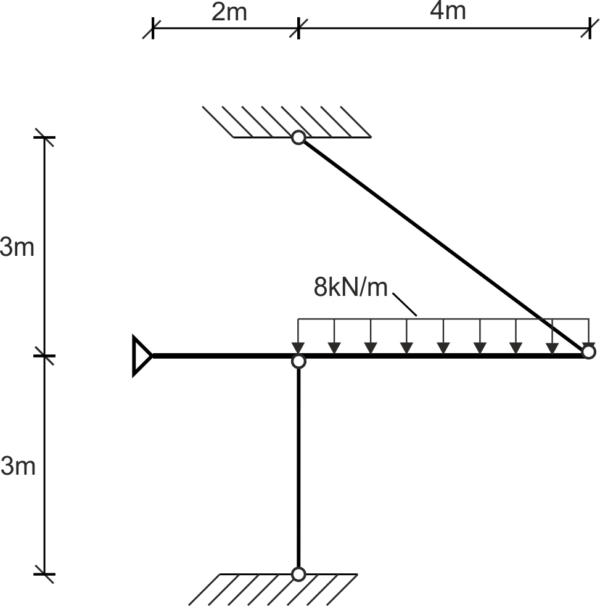
Belka zamocowana przegubowo i zaczepiona dwoma prętami obciążona jest obciążeniem ciągłym. Z warunku wytrzymałościowego policz średnicę prętów. Dane: \( A_1=A_2, E_1=2\cdot E_2, k_r=60\ MPa, k_c=90\ MPa \)

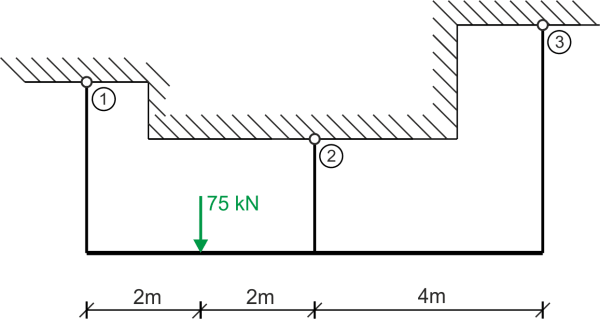
Drewniana belka podwieszona jest na trzech prętach - pierwszy i trzeci wykonane są ze stali, drugi jest miedziany, o długościach \( l_1=3m, l_2=2m, l_3=4m \) Oblicz jakie naprężenia powstają w prętach. Dane: \( k_{r_s}t=120 MPa, k_{r_m}=30 MPa, A_1=A_2=2\cdot A_3, E_2=105 GPa, E_1=E_3=210 GPa\)

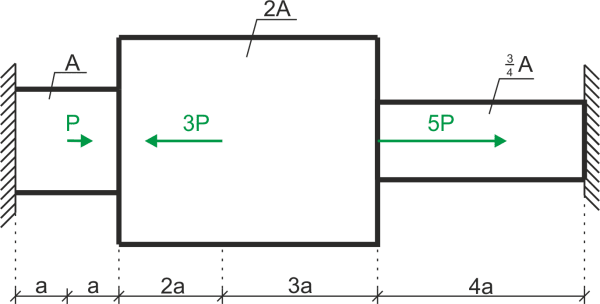
Policz siły normalne oraz zwymiaruj pole przekroju poprzecznego pręta. Dane: P, k

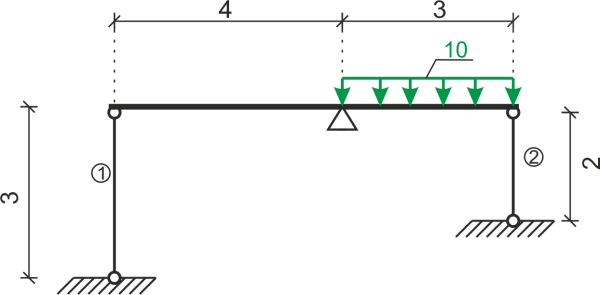
Oblicz średnicę cięgien na których podparta jest belka. Dane: \( E=210 GPa, A_1=A_2, k_r=100 MPa, k_c=120 MPa \)

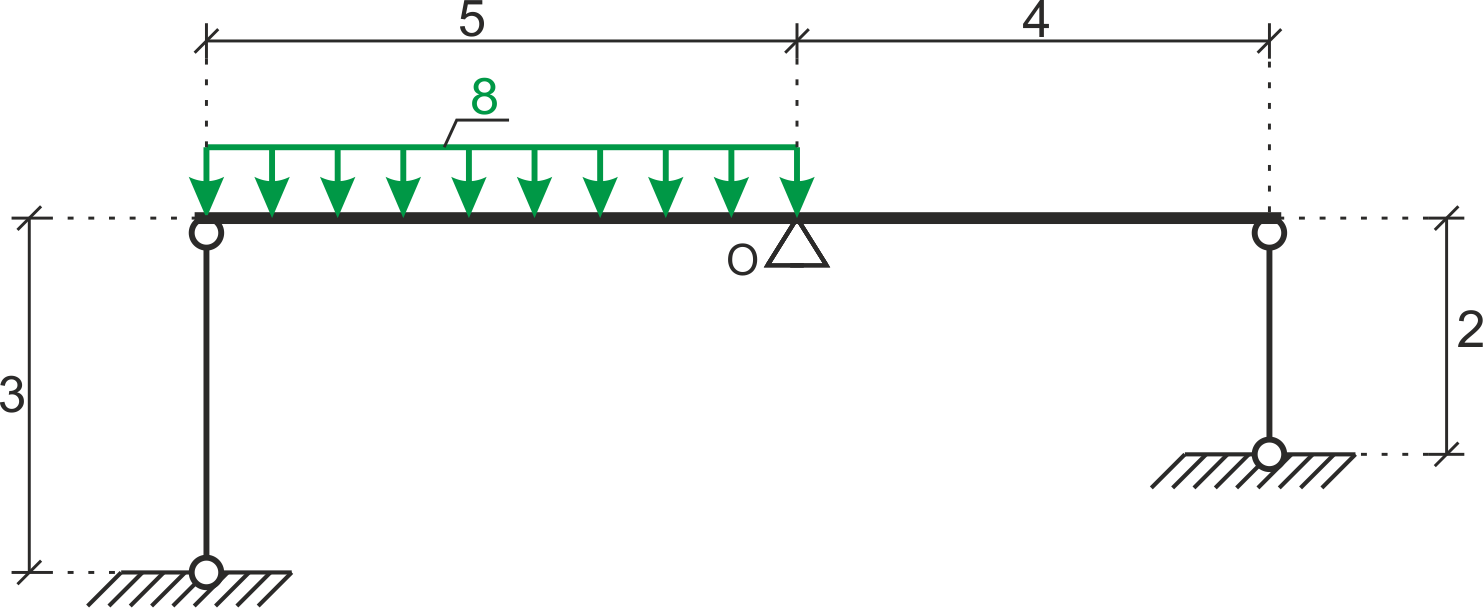
Oblicz siły w prętach podpierających belkę. Dane: \( A_1=A_2=A, E_1=E_2=E \)

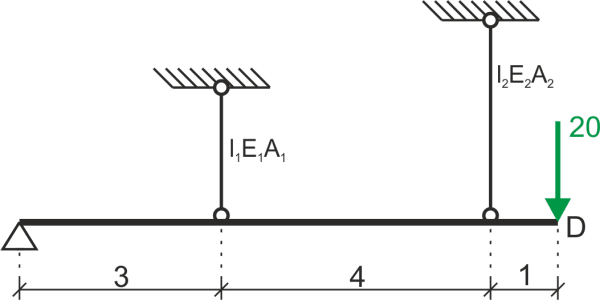
Oblicz pionowe przemieszczenie punktu D. Dane: \( E_1=2\cdot E_2, E_1=210\ GPa, l_1=2 m, l_2=3 m, 2\cdot A_1=A_2, A_1=20 cm^2 \)

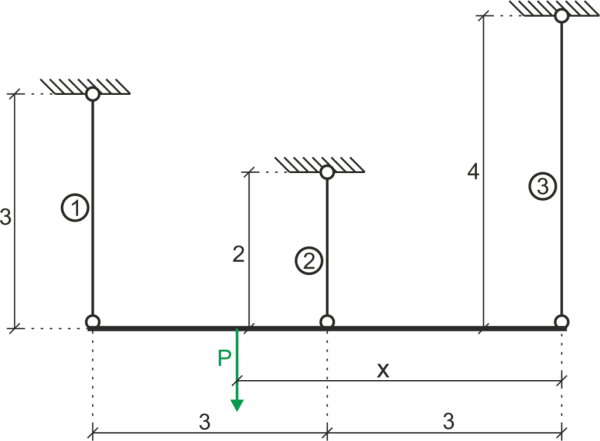
W jakiej odległości \(x\) od pręta numer \(3\) należy przyłożyć siłę \(P\) aby belka przemieściła się równolegle w dół. Dane: \( E_1=E_3=210 GPa, E_2=110 GPa, A_1=A_2=2\cdot A_3, P=20 kN\)

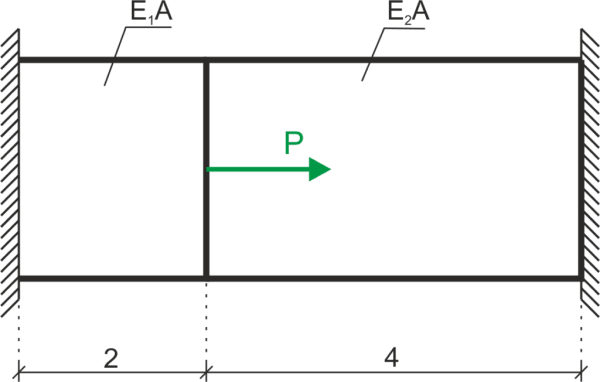
Oblicz siły normalne w poniższym pręcie. Dane: \(P=20 kN, E_1=2,1\cdot 10^5 MPa, E_2=1\cdot 10^5 MPa\)

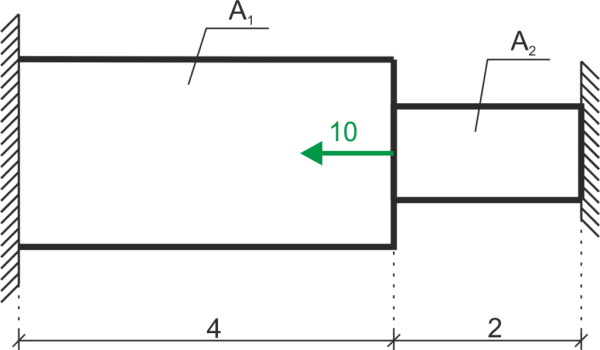
Oblicz reakcję w podporze po lewej stronie od obciążenia statycznego oraz termicznego oraz narysuj wykres sił normalnych. Policz naprężenia na dwóch przedziałach pręta. Dane:\(\Delta_T=20^o\ C, \alpha=1,2\cdot 10^{-5}, E=205\cdot 10^9, A_1=20\ cm^2, A_2=15\ cm^2\)

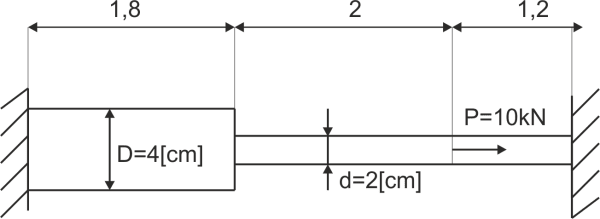
Oblicz i narysuj wykres sił normalnych, naprężeń oraz wydłużeń na wszystkich przedziałach dwustopniowego wałka. Dane jak na rysunku. Cały pręt został ogrzany o \(20^o C\). Współczynnik rozszerzalności termicznej \(\alpha =1,2\cdot 10^{-5}\)

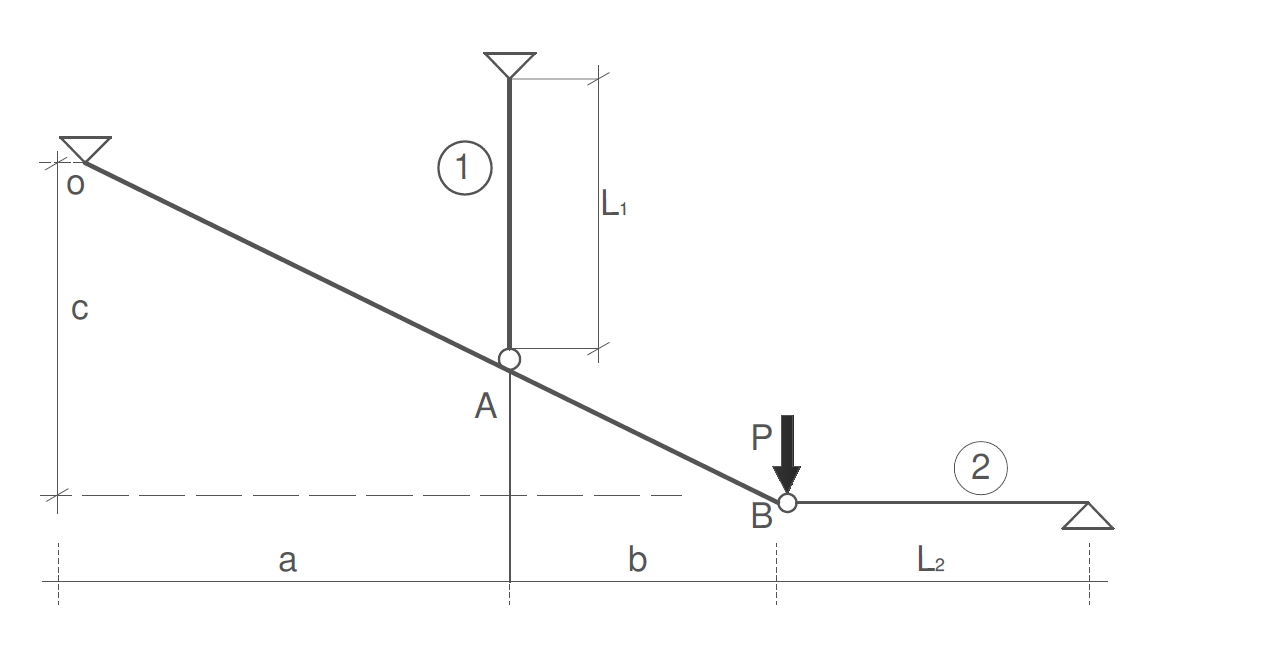
Nieodkształcalną belkę OAB podwieszono na dwóch sprężystych prętach wykonanych z materiału o module Younga \( E = 200 \, \text{GPa} \). Pole przekroju poprzecznego każdego pręta wynosi \( A_1 = A_2 = 10 \, \text{cm}^2 \), a ich długości \( L_1 = L_2 = 2 \, \text{m} \). Siła \( P = 150 \, \text{kN} \).

Wymiary: \( a = 4{,}5 \, \text{m} \), \( b = 2{,}5 \, \text{m} \), \( c = 3{,}5 \, \text{m} \)

Oblicz:
• siły w prętach kratowych: \( S_1, S_2 \) [kN]
• zmiany długości tych prętów: \( \Delta_1, \Delta_2 \) [mm]
• kąt obrotu sztywnej belki OAB: \( \omega \) [\(10^{-3}\) rad]

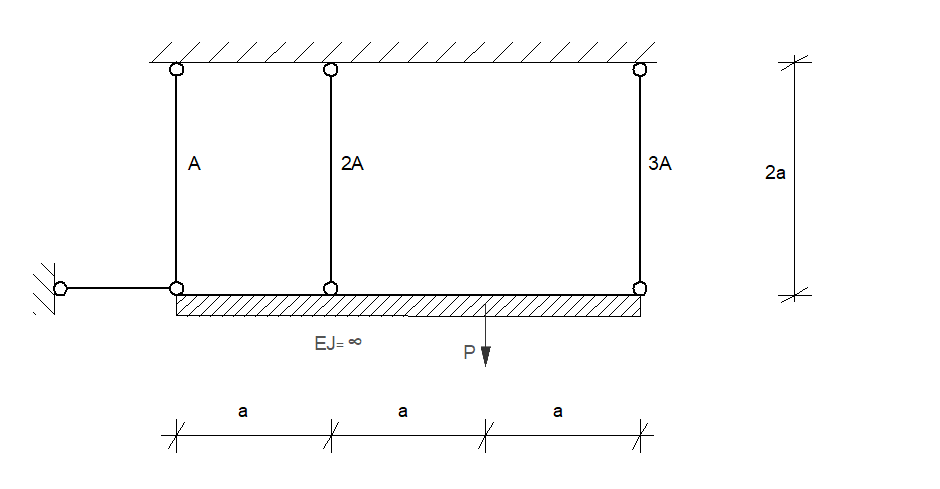
Wyznaczyć nośność sprężystą \( P = P_s \) i graniczną \( P = P_n \). Nośność graniczną wyznaczyć stosując podejście statyczne i kinematyczne. Sprawdzić, czy otrzymane rozwiązanie jest kompletne. Ponadto wyznaczyć współczynnik rezerwy nośności \( m = \frac{P_n}{P_s} \). Podając ostateczne wyniki, przyjąć: \( a = 1 \, \text{m} \), \( A = 4 \, \text{cm}^2 \), \( R_{pl} = 200 \, \text{MPa} \).

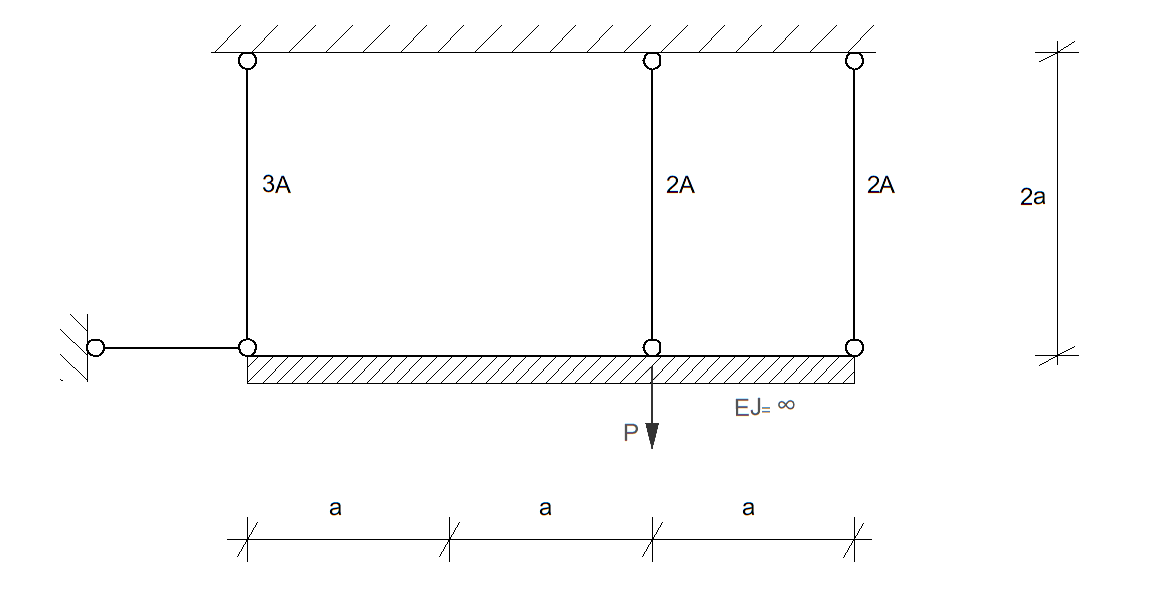
Stosując metodę stanów granicznych (podejście statyczne), wyznaczyć wartość siły \( P = P_n \), przy której zostanie wyczerpana nośność układu. Przyjąć: \( a = 1\, \text{m} \), \( A = 4\, \text{cm}^2 \), \( R_e = 200\, \text{MPa} \).

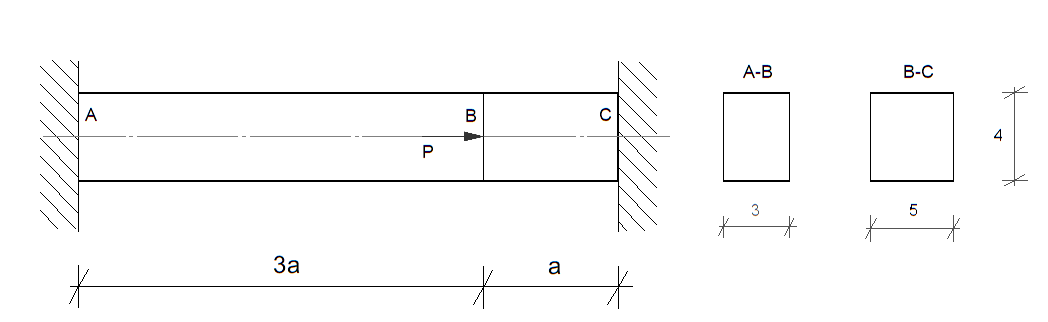
Wyznaczyć taką wartość obciążenia \( P = P_s \), przy którym największe naprężenie w pręcie osiągnie wartość równą \( R_e \). Następnie, posługując się metodą stanów granicznych nośności, wyznaczyć taką wartość obciążenia \( P = P_n \), przy którym pręt osiągnie stan graniczny nośności. Przyjąć: \( a = 1\,\text{m} \), \( R_e = 240\,\text{MPa} \), \( E = 205\,\text{GPa} \)i wymiary przekroju pręta podane na rysunku. Wynik podać w kN. Wyznaczyć ponadto stosunek \( \frac{P_n}{P_s} \).

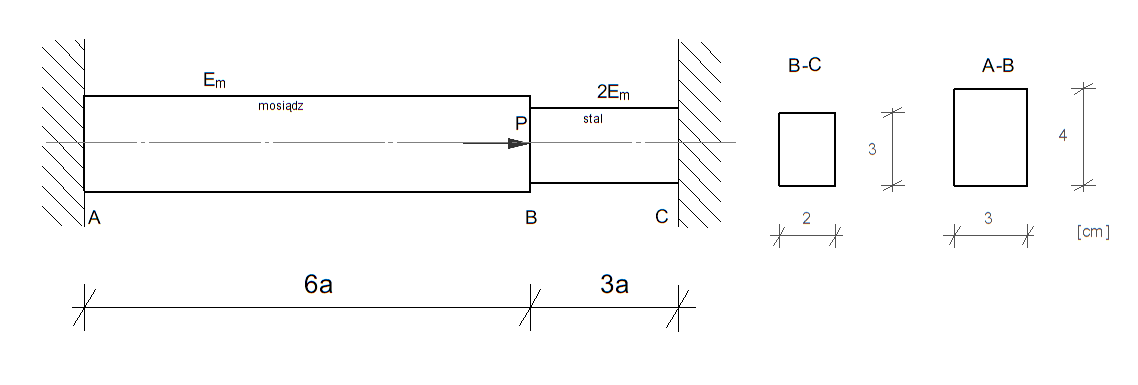
Dany jest pręt o zmiennym przekroju poddany działaniu osiowej siły \( P \). Na odcinku \( AB \) pręt wykonano z mosiądzu o \( E_m = 1 \cdot 10^5 \ \text{MPa} \) i \( R_{e1} = 200 \ \text{MPa} \), oraz na odcinku \( BC \) ze stali o \( E = 2E_m = 2 \cdot 10^5 \ \text{MPa} \) i \( R_{e2} = 250 \ \text{MPa} \). Wyznaczyć taką wartość obciążenia \( P = P_p \), przy którym największe naprężenie osiągnie wartość równą \( R_e \). Następnie, posługując się metodą stanów granicznych, wyznaczyć taką wartość \( P = P_r \), przy którym pręt osiągnie stan graniczny nośności. Wyznaczyć stosunek \( \frac{P_p}{P_r} \). Przyjąć \( a = 0{,}2 \ \text{m} \).

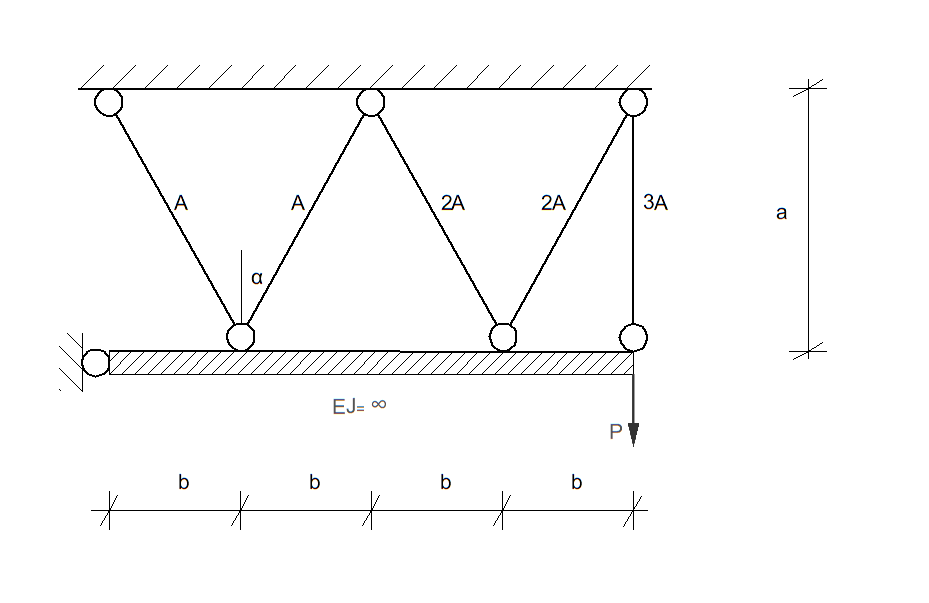
Stosując metodę stanów granicznych (podejście statyczne), wyznaczyć wartość siły \( P = P_n \), przy której zostanie wyczerpana nośność przedstawionego obok układu prętowego.

Po wyznaczeniu siły \( P_n \), stosując podejście kinematyczne, wykazać, że podane rozwiązanie jest ścisłe.

Przyjąć: \( a = 3 \ \text{m}, \quad b = 2 \ \text{m}, \quad A = 3 \ \text{cm}^2, \quad R_{pl} = 250 \ \text{MPa} \).