Versión YT

Versión clásica

Distribución de fuerzas P en componentes

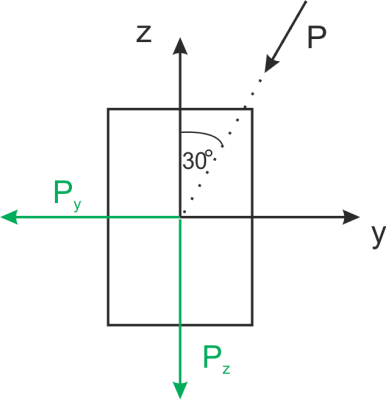\begin{aligned} &P_y=P sinα=5kN\\ &P_y=P cosα=8,66kN\\ \end{aligned}

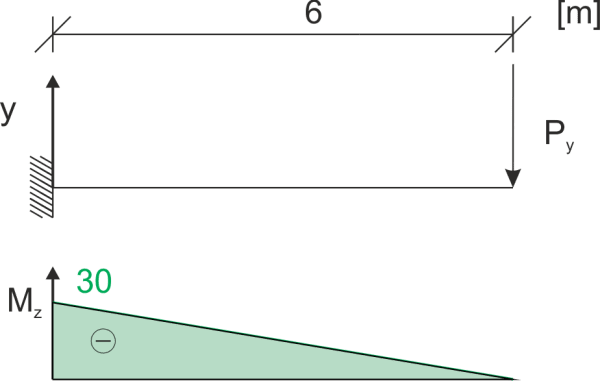
Carga en el plano xz y xy, gráficos de momentos flexionantes

\begin{aligned} &M_y=-P_z⋅6-\frac{1}{2}⋅5⋅6^2=-141,96kNm \end{aligned}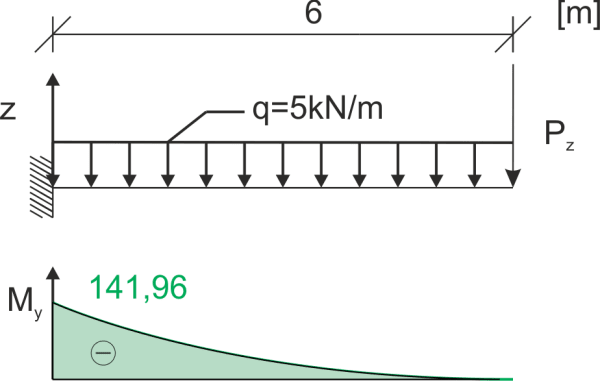 \begin{aligned} &M_z=-P_y⋅6=-26\ kNm \end{aligned}

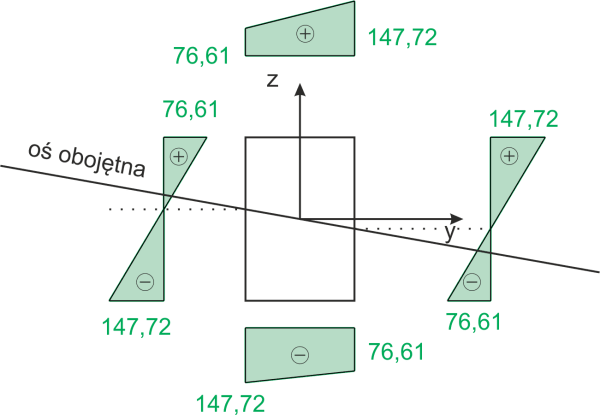
Vectores de momentos, designación de puntos característicos de la sección transversal

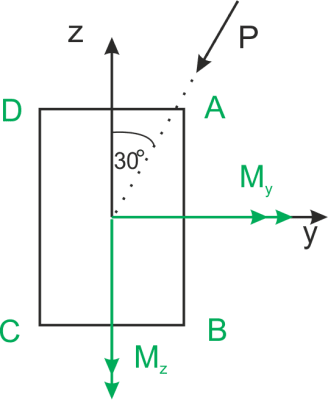
Tensiones normales

\begin{aligned} &\sigma=\frac{M_y}{I_y}z+\frac{M_z}{I_z}y\\ &I_y=\frac{bh^3}{12}=\frac{2a\cdot\left(3a\right)^3}{12}=\frac{9}{2}a^4\\ &I_z=\frac{hb^3}{12}=\frac{3a\cdot\left(2a\right)^3}{12}=2a^4\\ \end{aligned}

Determinación de la ecuación de la línea de neutral

\begin{aligned} &\sigma=0\\ &\sigma_{max}=\frac{141,92\cdot{10}^3}{\frac{9}{2}a^4}\cdot1,5a+\frac{30\cdot{10}^3}{2a^4}\cdot a\\ &z=-0,475y\\ \end{aligned}

Basta con determinar dos puntos para trazar el perfil de la función lineal

\begin{aligned} y=0,z=0 y=1,z=-0,475 \end{aligned}

Condición de resistencia σ_max≤k_g

\begin{aligned} &\sigma_{max}=\frac{141,92\cdot{10}^3}{\frac{9}{2}a^4}\cdot1,5a+\frac{30\cdot{10}^3}{2a^4}\cdot a\le k_g\\ &a=0,075m=7,5cm\\ \end{aligned}

Tensiones en puntos característicos

\begin{aligned} &σ_A=147,72MPa\\ &σ_B=-76,61MPa\\ &σ_C=-147,72MPa\\ &σ_D=76,61MPa\\ \end{aligned

Gráfico de tensiones normales