Solución
Solución YT
a partir de las 18:45Solución clásica
Descomposición de la fuerza en la barra AC en sus componentes horizontal y vertical.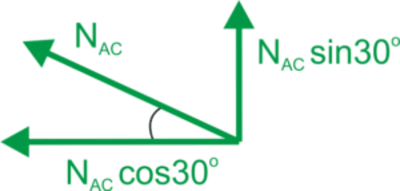
Ecuaciones de equilibrio estático para el nodo A. \begin{aligned} &\sum{Y}=0\\ &N_{AC}\cdot\sin30^{o}=0\\ &N_{AC}=2G\\ &\sum{X}=0\\ &-N_{AB}-N_{AC}\cdot\cos30^{o}=0\\ &N_{AB}=-2G\cdot\frac{\sqrt3}{2}\\ &N_{AB}=-G\sqrt3\\ \end{aligned} Criterio de resistencia
Tomamos en cuenta las elongaciones y acortamientos de las barras (en sus ejes).
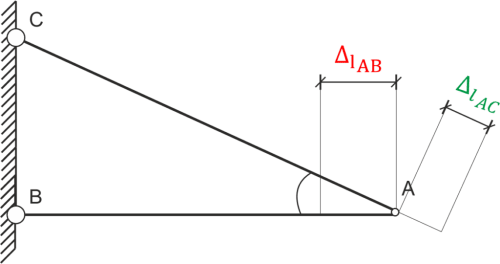
Calculamos la elongación de la barra AC (fuerza positiva en la barra) y el acortamiento de la barra AB (fuerza negativa - barra comprimida). \begin{aligned} \Delta l &= \frac{Nl}{EA} \\ \Delta l_{AB} &= \frac{-50 \cdot \sqrt{3} \cdot 10^{3} \cdot 1.2}{E_{m} \cdot a^{2}} = \frac{-50 \cdot \sqrt{3} \cdot 10^{3} \cdot 1.2}{1.15 \cdot 10^{11} \cdot 0.047^{2}} = -4.09 \times 10^{-4} \ m = -0.409 \ mm \end{aligned} Calculamos la longitud de la barra AC y su elongación. \begin{aligned} &\frac{1,2}{|AC|}=\cos30^{o} & \\ & |AC|=\frac{1,2}{\cos30^{o}}=1,386\\ &\Delta l_{AC}=\frac{50\cdot 2\cdot 10^{3}\cdot |AC|}{E_{s}\cdot\frac{\pi d^{2}}{4}}=\frac{50\cdot 2\cdot 10^{3}\cdot 1,386\cdot 4}{2,1\cdot 10^{11}\cdot\pi\cdot 0,03^{2}}=9,337\cdot 10^{-4} \ m=0,934 \ mm\\ \end{aligned} Marcamos la línea permitida de desplazamiento de las barras alargadas/comprimidas y encontramos su intersección - el punto A se desplazará a este lugar finalmente.
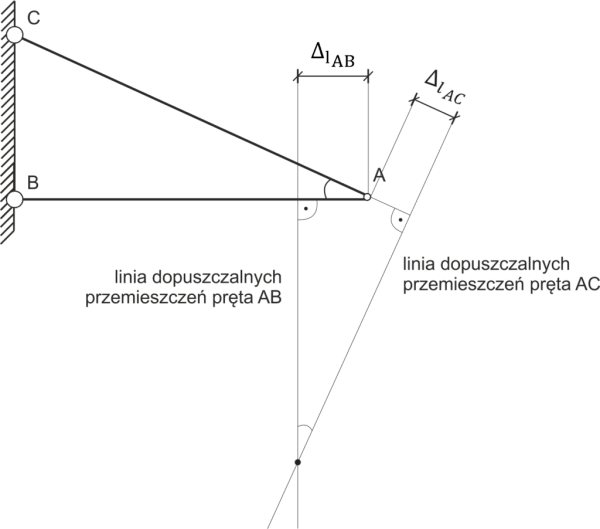
Observamos el triángulo verde, describimos dos de sus lados como a, b y notamos que es similar al triángulo pequeño a', b', \( \Delta l_{AB} \).
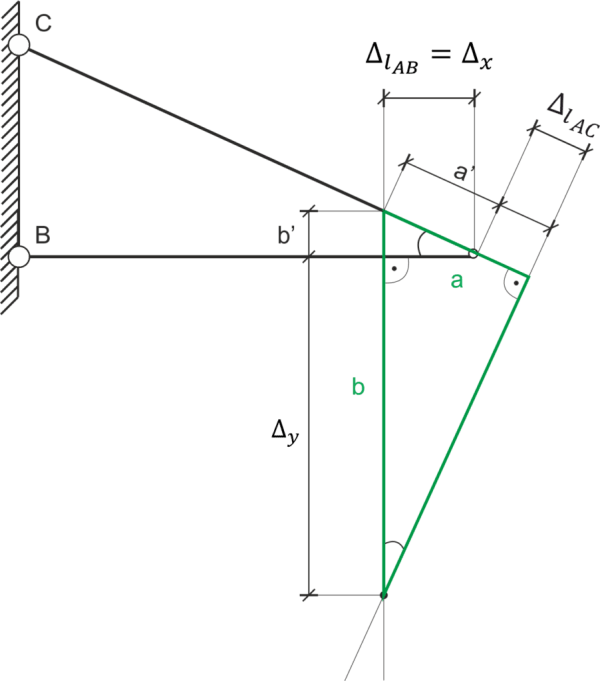
Calculamos el lado a. \begin{aligned} &a=a' + |\Delta l_{AC}|\\ &|\Delta l_{AC}|=0,934 \ mm\\ &\frac{|\Delta l_{AB}|}{a'}=\cos30^{o}\\ &a'=\frac{0,409}{\frac{\sqrt3}{2}}=0,47 \ mm\\ &a=0,47 + 0,934 = 1,404 \ mm \end{aligned} Calculamos el lado b. \begin{aligned} &b=b' + \Delta_{y}\\ &\frac{b'}{a'}=sin30^{o}\\ &b'=0,47\cdot 0,5 = 0,235 \ mm\\ &\frac{a}{b}=\sin30^{o}\\ &b=\frac{a}{sin30^{o}}=\frac{1,404}{0,5}\\ &b=2,808 \ mm\\ \end{aligned} Calculamos el desplazamiento vertical y horizontal del punto A. \begin{aligned} &\Delta_{y}=b-b'\\ &\Delta_{y}=2,808 - 0,235 = 2,573 \ mm\\ &\Delta_{x}=\Delta l_{AB} = 1,438 \ mm\\ \end{aligned}
Si tienes preguntas, comentarios, o crees que has encontrado un error en esta solución, por favor envíanos un mensaje a kontakt@edupanda.pl.
