Solution
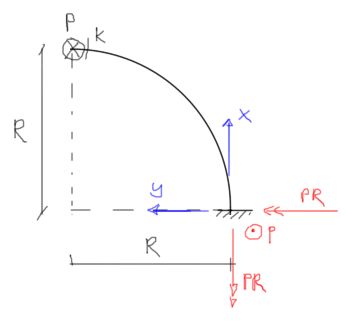
Dans l'état P, les réactions et les formules pour les forces internes sont les suivantes :
 \begin{aligned}
&M_{g} = -P \cdot R \cdot \sin (\alpha) \\
&M_{s} = P \cdot R \cdot(1-\cos (\alpha))
\end{aligned}
\begin{aligned}
&M_{g} = -P \cdot R \cdot \sin (\alpha) \\
&M_{s} = P \cdot R \cdot(1-\cos (\alpha))
\end{aligned}
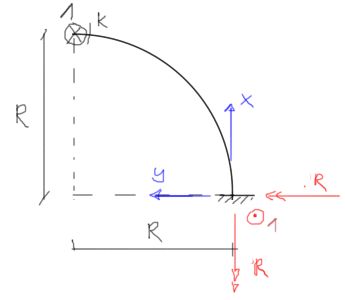
Dans l'état unitaire, les réactions et les formules pour les forces internes sont les suivantes :
 \begin{aligned}
&m_{g} = -R \cdot \sin (\alpha) \\
&m_{s} = R \cdot(1-\cos (\alpha))
\end{aligned}
\begin{aligned}
&m_{g} = -R \cdot \sin (\alpha) \\
&m_{s} = R \cdot(1-\cos (\alpha))
\end{aligned}
Je calcule le déplacement du point K en utilisant la formule Maxwell-Mohr :
\begin{aligned} &y = \frac{1}{E I} \int_{0}^{\frac{\pi}{2}}(-P \cdot R \cdot \sin (\alpha)) \cdot(-R \cdot \sin (\alpha)) \mathrm{d} \alpha + \frac{1}{G I} \int_{0}^{\frac{\pi}{2}} P \cdot R \cdot(1-\cos (\alpha)) \cdot R \cdot(1-\cos (\alpha)) \mathrm{d} \alpha \\ &y = \frac{1}{E I} \int_{0}^{\frac{\pi}{2}} P \cdot R^{2} \cdot \sin (\alpha)^{2} \mathrm{~d} \alpha + \frac{1}{G I} \int_{0}^{\frac{\pi}{2}} P \cdot R^{2} \cdot(\cos (\alpha)-1)^{2} \mathrm{~d} \alpha \end{aligned}Où les valeurs des intégrales sont les suivantes :
\begin{aligned} &\int_{0}^{\frac{\pi}{2}} P \cdot R^{2} \cdot \sin (\alpha)^{2} \mathrm{~d} \alpha \rightarrow \frac{P \cdot R^{2} \cdot \pi}{4} \\ &\int_{0} P \cdot R^{2} \cdot(\cos (\alpha)-1)^{2} \mathrm{~d} \alpha \rightarrow \frac{3 \cdot P \cdot R^{2} \cdot \pi}{4}-2 \cdot P \cdot R^{2} \end{aligned}Donc finalement,
\begin{aligned} y=\frac{7 \cdot P \cdot R^{2} \cdot \pi}{4}-4 \cdot P \cdot R^{2} \end{aligned}
Si vous avez des questions, des remarques ou si vous pensez avoir trouvé une erreur dans cette solution, veuillez nous envoyer un message à kontakt@edupanda.pl.
