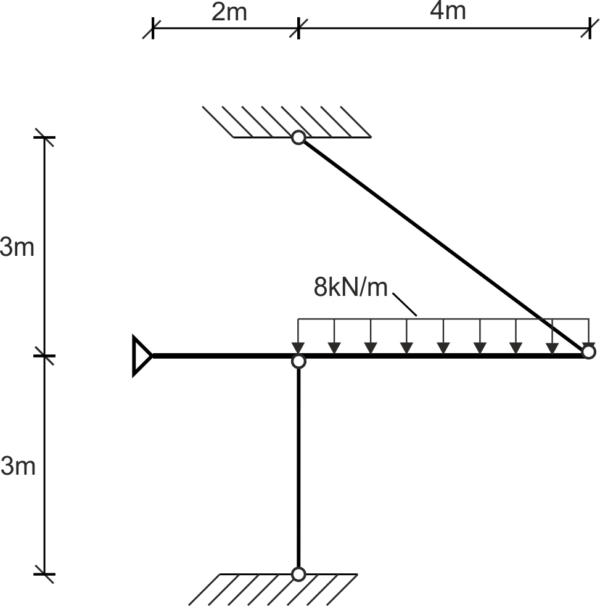
Solution
Je marque les réactions de support et les forces dans les barres treillis
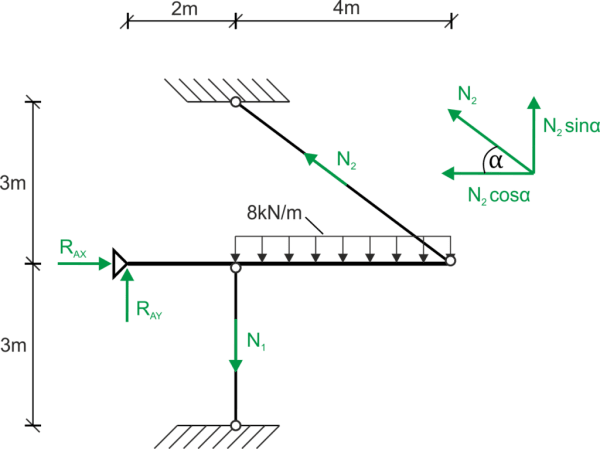
J'écris une équation d'équilibre statique - une équation dans laquelle les inconnues sont les forces dans les barres \( N_1, N_2 \) \begin{aligned} &\sum{M_{A}}=0\\ &N_{1}\cdot 2 - N_{2}\cdot \sin\alpha\cdot 6 + 8\cdot 4\cdot 4=0\\ &N_{1}=3N_{2}\cdot\sin\alpha - 64\\ &\sin\alpha=\frac{3}{5} & \cos\alpha=\frac{4}{5}\\ &N_{1}=1,8N_{2}-64\\ \end{aligned} Je dessine un schéma de déplacement pour énoncer la condition géométrique (la relation entre les déplacements par similitude des triangles)
Les barres peuvent s'allonger le long de leurs axes, mais la ligne admissible de déplacement de l'extrémité allongée/raccourcie de la barre est perpendiculaire à l'axe de la barre.
De plus, je me souviens que chaque point de la poutre horizontale indéformable peut se trouver perpendiculairement à cet axe.
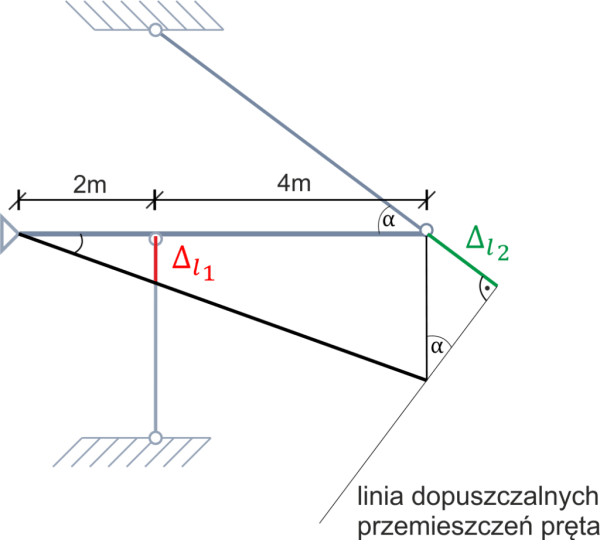
Condition géométrique \begin{aligned} &\frac{f_{B}}{2}=\frac{f_{A}}{6}\\ &\frac{\Delta l_{2}}{f_{A}}=\sin\alpha \ \ \ \Rightarrow \ \ \ f_{A}=\frac{\Delta l_{2}}{\sin\alpha}\\ &f_{B}=\Delta l_{1}\\ &\frac{\Delta l_{1}}{2}=\frac{\frac{\Delta l_{2}}{\sin\alpha}}{6}\\ &6\sin\alpha\cdot\Delta l_{1}=2\cdot\Delta l_{2}\\ &6\cdot 0,6\cdot\frac{-N_{1}\cdot 3}{E_{1}\cdot A_{1}}=2\cdot\frac{N_{2}\cdot 5}{E_{2}\cdot A_{2}}\\ &\frac{-10,8N_{1}}{2E_{2}\cdot A_{2}}=\frac{10N_{2}}{E_{2}\cdot A_{2}} \ \ \ \ \ \ \ \ |\cdot E_{2}A_{2}\\ &-5,4N_{1}=10N_{2}\\ &N_{1}=-1,85N_{2} \end{aligned} Nous obtenons une deuxième relation entre \(N_1 \) et \(N_2 \), revenons à la première relation et calculons les forces dans les barres
\begin{aligned} &N_{1}=1,85N_{2}-64\\ &-1,85N_{2}=1,8N_{2}-64\\ \\ &N_{2}=17,53 \ kN\\ &N_{1}=-32,43 \ kN\\ \end{aligned} Condition de résistance \begin{aligned} &\sigma=\frac{|N|}{A}\le k\\ \end{aligned} \begin{array}{ll} \sigma_{1}=\frac{32,43 \cdot 10^{3}}{A} \leq 90 \cdot 10^{6} & \Rightarrow A \geq 3,6 \cdot 10^{-4} \mathrm{~m}^{2} \\ \sigma_{2}=\frac{17,53 \cdot 10^{3}}{A} \leq 60 \cdot 10^{6} & \Rightarrow A \geq 2,92 \cdot 10^{-4} \mathrm{~m}^{2} \\ \end{array} Je choisis la première condition, j'accepte: \begin{array}{ll}A=3,65 \cdot 10^{-4} \mathrm{~m}^{2} & \Rightarrow d=0,0215 \mathrm{~m}=2,15 \mathrm{~cm} \\ A=\frac{\pi d^{2}}{4} \end{array}

J'écris une équation d'équilibre statique - une équation dans laquelle les inconnues sont les forces dans les barres \( N_1, N_2 \) \begin{aligned} &\sum{M_{A}}=0\\ &N_{1}\cdot 2 - N_{2}\cdot \sin\alpha\cdot 6 + 8\cdot 4\cdot 4=0\\ &N_{1}=3N_{2}\cdot\sin\alpha - 64\\ &\sin\alpha=\frac{3}{5} & \cos\alpha=\frac{4}{5}\\ &N_{1}=1,8N_{2}-64\\ \end{aligned} Je dessine un schéma de déplacement pour énoncer la condition géométrique (la relation entre les déplacements par similitude des triangles)
Les barres peuvent s'allonger le long de leurs axes, mais la ligne admissible de déplacement de l'extrémité allongée/raccourcie de la barre est perpendiculaire à l'axe de la barre.
De plus, je me souviens que chaque point de la poutre horizontale indéformable peut se trouver perpendiculairement à cet axe.

Condition géométrique \begin{aligned} &\frac{f_{B}}{2}=\frac{f_{A}}{6}\\ &\frac{\Delta l_{2}}{f_{A}}=\sin\alpha \ \ \ \Rightarrow \ \ \ f_{A}=\frac{\Delta l_{2}}{\sin\alpha}\\ &f_{B}=\Delta l_{1}\\ &\frac{\Delta l_{1}}{2}=\frac{\frac{\Delta l_{2}}{\sin\alpha}}{6}\\ &6\sin\alpha\cdot\Delta l_{1}=2\cdot\Delta l_{2}\\ &6\cdot 0,6\cdot\frac{-N_{1}\cdot 3}{E_{1}\cdot A_{1}}=2\cdot\frac{N_{2}\cdot 5}{E_{2}\cdot A_{2}}\\ &\frac{-10,8N_{1}}{2E_{2}\cdot A_{2}}=\frac{10N_{2}}{E_{2}\cdot A_{2}} \ \ \ \ \ \ \ \ |\cdot E_{2}A_{2}\\ &-5,4N_{1}=10N_{2}\\ &N_{1}=-1,85N_{2} \end{aligned} Nous obtenons une deuxième relation entre \(N_1 \) et \(N_2 \), revenons à la première relation et calculons les forces dans les barres
\begin{aligned} &N_{1}=1,85N_{2}-64\\ &-1,85N_{2}=1,8N_{2}-64\\ \\ &N_{2}=17,53 \ kN\\ &N_{1}=-32,43 \ kN\\ \end{aligned} Condition de résistance \begin{aligned} &\sigma=\frac{|N|}{A}\le k\\ \end{aligned} \begin{array}{ll} \sigma_{1}=\frac{32,43 \cdot 10^{3}}{A} \leq 90 \cdot 10^{6} & \Rightarrow A \geq 3,6 \cdot 10^{-4} \mathrm{~m}^{2} \\ \sigma_{2}=\frac{17,53 \cdot 10^{3}}{A} \leq 60 \cdot 10^{6} & \Rightarrow A \geq 2,92 \cdot 10^{-4} \mathrm{~m}^{2} \\ \end{array} Je choisis la première condition, j'accepte: \begin{array}{ll}A=3,65 \cdot 10^{-4} \mathrm{~m}^{2} & \Rightarrow d=0,0215 \mathrm{~m}=2,15 \mathrm{~cm} \\ A=\frac{\pi d^{2}}{4} \end{array}
Si vous avez des questions, des remarques ou si vous pensez avoir trouvé une erreur dans cette solution, veuillez nous envoyer un message à kontakt@edupanda.pl.